PKU 1899
http://acm.pku.edu.cn/JudgeOnline/problem?id=1899
题意:
若干个矩形, 如果有联系(相交和相邻);则合并成一个大的矩形,求合并完以后矩形的面积。
此题很显然的并查集,如果两个矩形有连理则合并。。。。那么最后有几个集合就还剩下几个矩形,求其面积即可。
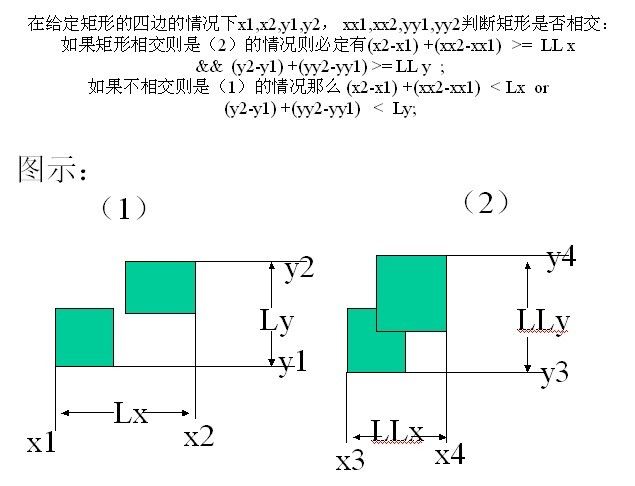
那么如何判断两个矩形是否相交则成为难点了,具体如下:
那么此题就很简单了,代码如下:
#include<iostream> using namespace std; const int MAXN = 101 ; int xmin[MAXN], xmax[MAXN], ymin[MAXN], ymax[MAXN]; int n, nx, ny, x, y, r, x1, y1, xx, yy, xp, yp; int p[MAXN] ; int find(int x) { if(x != p[x]) p[x] = find(p[x]) ; return p[x] ; } void Union(int x,int y) { int rx = find(x) , ry = find(y) ; p[ry] = rx ; xmin[rx] = min(xmin[rx],xmin[ry]) ; ymin[rx] = min(ymin[rx],ymin[ry]) ; xmax[rx] = max(xmax[rx],xmax[ry]) ; ymax[rx] = max(ymax[rx],ymax[ry]) ; } int main() { while(~scanf("%d%d%d",&nx,&ny,&n)) { for(int i=0;i<n;i++) { scanf("%d%d%d",&x,&y,&r) ; xmin[i] = x - r, xmax[i] = x + r, ymin[i] = y - r, ymax[i] = y + r ; } for(int i=0;i<n;i++) p[i] = i ; bool more = true ; while(more) { more = false ; for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(i == j) continue ; int xp = find(i); int yp = find(j); if(xp != yp) { /* 判断矩形相交的快速方法: 如果相交 就可以合并成一个大矩形。 求出大矩形的两边。。 然后求出相邻的时候的边长。。比较之。。。 */ xx=max(xmax[xp],xmax[yp])-min(xmin[xp],xmin[yp]) ; yy=max(ymax[xp],ymax[yp])-min(ymin[xp],ymin[yp]) ; x1=xmax[xp]-xmin[xp]+xmax[yp]-xmin[yp] ; y1=ymax[xp]-ymin[xp]+ymax[yp]-ymin[yp] ; if(xx<=x1&&yy<=y1) { more = true ; Union(i,j) ; } } } } } int res = 0 ; for(int i=0;i<n;i++) { if(i == find(i)) res += (xmax[i] - xmin[i]) * (ymax[i] - ymin[i]) ; } printf("%d/n",nx*ny - res); } return 0; }