后缀数组(一)
一直没理解后缀数组是个什么样的东西……
今天来理解一下:
论文前面的东西介绍的很详细,主要解释一下代码作用,我这里的模板………『是fsf的』
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#define Rep(i,n) for(int i = 1; i <= n ; i ++)
#define RepG(i,x) for(int i = head[x] ;~ i ; i = edge[i].next)
#define Rep_d(i,n) for(int i = n ; i > 0 ; i --)
#define Rep_0(i,n) for(int i = 0 ; i < n ; i ++)
#define RD(i,x,n) for(int i = x; i <= n ; i ++)
#define CLR(a,b) memset(a,b,sizeof(a))
#define RDD(i,x,n) for(int i = x; i >= n; i --)
#define lc ch[0]
#define rc ch[1]
#define v edge[i].to
#define ulfc t[u.lc]
#define urtc t[u.rc]
using namespace std;
const int inf = 1 << 30;
typedef long long ll;
int read(){
char ch = getchar();
while((ch < '0' || ch > '9') && ch != '-')ch = getchar ();
int x = 0;
bool flag = 0;
if(ch == '-')ch = getchar(),flag = 1;
while(ch >= '0' && ch <= '9')x = (x << 1) + (x << 3) + ch - '0',ch = getchar ();
return flag ? -x : x;
}
const int N = 100005;
int ta[N],tb[N],c[N],ht[N],Rank[N],sa[N];
void Build_sa(char *s,int n){
CLR(ta,0),CLR(tb,0);
int *x = ta,*y = tb;int m = 300;
Rep(i,n)++ c[x[i] = s[i]];
Rep(i,m)c[i] += c[i - 1];
Rep_d(i,n)sa[c[x[i]] --] = i;
//按长度为1的排序
for(int k = 1, p = 0;p < n;k <<= 1,m = p)
{
Rep(i,m)c[i] = 0;c[0] = p = 0;
RD(i,n - k + 1,n)y[++ p] = i;
Rep(i,n)if(sa[i] > k)y[++ p] = sa[i] - k;
//按y排好序
Rep(i,n)++ c[x[y[i]]];
Rep(i,m)c[i] += c[i - 1];
Rep_d(i,n)sa[c[x[y[i]]] --] = y[i];
//按第一关键字排序
int i;
for(i = 2,p = 1,y[sa[1]] = 1;i <= n;i ++)
y[sa[i]] = (x[sa[i]] == x[sa[i - 1]] && x[sa[i] + k] == x[sa[i - 1] + k]) ? p : ++ p;
swap(x,y);
//把Rank值保存在x数组中,p为不同串的个数
}
Rep(i,n)Rank[sa[i]] = i;
for(int i = 1,j,k; i <= n;i ++)
{
if(Rank[i] < n){
j = sa[Rank[i] + 1];
for(k = max(ht[Rank[i - 1]] - 1,0);s[i + k] == s[j + k];++ k);
ht[Rank[i]] = k;
}
}
}
char s[200005];
int main (){
scanf("%s",s + 1);
int n = strlen(s + 1);
Build_sa(s,n);
Rep(i,n)printf("%d ",sa[i]);
puts("");
Rep(i,n - 1)printf("%d ",ht[i]);
puts("");
return 0;
}
前面还没有进入主要的循环时,就是一个按照长度为1的子串进行计数排序。
CLR(ta,0),CLR(tb,0);
int *x = ta,*y = tb;int m = 300;
Rep(i,n)++ c[x[i] = s[i]];
Rep(i,m)c[i] += c[i - 1];
Rep_d(i,n)sa[c[x[i]] --] = i;这个计数排序就不讲了吧……
for(int k = 1, p = 0;p < n;k <<= 1,m = p)这个是倍增的过程,其主要目的就是为了倍增……
Rep(i,m)c[i] = 0;c[0] = p = 0;
RD(i,n - k + 1,n)y[++ p] = i;
Rep(i,n)if(sa[i] > k)y[++ p] = sa[i] - k;这个是在把第二关键字排序,得到第二关键字的”Sa”。
这样排序为什么能排成功呢……
因为你想……
1.如果该后缀长度小于k,那么也就意味着,它整个后缀只有第一关键字,所以它的第二关键字都是0,并且我们规定,在相等时,长度比较小的更大,而由于我们一会计数排序之后肯定要倒着走,所以我们把长度小的放前面。
2.如果该后缀标号大于k,它的第二关键字必然通过上一次的Sa可以得到。
那么y显然就是在长度为2*k的意义下的后半段的’Sa’了。
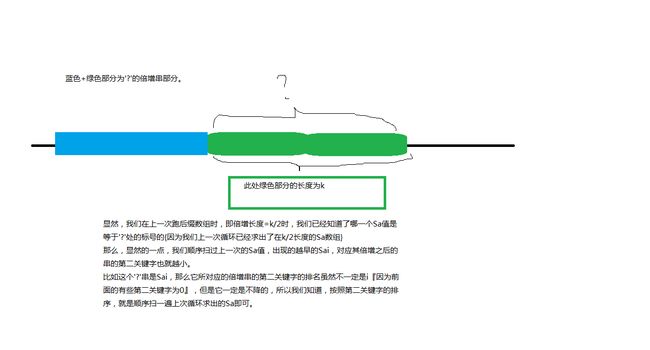
这里,由于其后缀标号大于k,那么前面蓝色部分的长度是可以达到k的,并且很显然的一点是,此时一定是把所有后缀加入在这个y中的。
接下来是这句话:
Rep(i,n)++ c[x[y[i]]];
Rep(i,m)c[i] += c[i - 1];
Rep_d(i,n)sa[c[x[y[i]]] --] = y[i];这个计数排序,在第二关键字的基础上将第一关键字排序,求出Sa。
但是……慢着?
x数组好像还没有用过?
仔细考虑下x数组的意义:
首先:x数组显然是当前2 * k的长度下的前半段的Rank值。
即:x数组是长度为k的意义下的Rank值,它保留的是上一次的Rank。
问题:那么排序排出的Sa是在什么长度意义下的?
Sa是把x和y拼一起,即k * 2 意义下的,也就是下一次的k的意义下的。
那么我们只要求出这次的Sa数组,就能在下一次循环中求出y数组。
那么我们只要再记录一下本次的Rank就行了。
但是我们不仅要记录Rank还要记录这次的Rank有没有以当前的长度排不出来后缀的先后顺序的情况。
int i;
for(i = 2,p = 1,y[sa[1]] = 1;i <= n;i ++)
y[sa[i]] =
(x[sa[i]] == x[sa[i - 1]] && x[sa[i] + k] == x[sa[i - 1] + k]) ?
p : ++ p;
swap(x,y);压行压的很到位……
以下摘自论文:
这里要注意的是,可能有多个字符串的rank 值是相同的,所以必须比较两个字符串是否完全相同,y 数组的值已经没有必要保存,为了节省空间,这里用y 数组保存rank值。这里又有一个小优化,将x 和y 定义为指针类型,复制整个数组的操作可以用交换指针的值代替,不必将数组中值一个一个的复制。
也就是说,这两行代码只是用来求Rank值的。
我们可以在求Rank值的过程中直接判断它有没有排好序。
循环的初始阶段,Rank值为1的『为了不让数组访问到0』要先弄好……
我们如何判断排名:
我们直接判断这个:x[sa[i]] == x[sa[i - 1]] && x[sa[i] + k] == x[sa[i - 1] + k]是否为真即可。
(从神犇那里问完回来后知道)这个数组是不会越界的。
因为前面一个条件如果成立那么一定是sa[i] , sa[i - 1] + k <= n
的,如果不成立,那么就直接判断为假了。
这样就能求出后缀数组Sa了。
又有Rank[Sa[i]] = i;
然后就没了……
至于后缀数组有什么用……?
我们下篇博客再讲。
我决定还是讲下height数组:
定义height[i] = LCP{suf(Sa[i - 1]),suf(Sa[i])};
定义h[i] = height[Rank[i]]];
如果我们暴力求height的话,O(n^2)滚粗。
然后我们发现h数组有个性质:
h[i] >= h[i - 1] - 1;
对于h[i - 1] <= 1显然。
对于h[i - 1] >= 2:
height数组:height[i]=Suffix(sa[i-1])和Suffix(sa[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀。
h数组:h[i]=height[rank[i]]=Suffix(i)和在它前一名的后缀的最长公共前缀。
证明:设Suffix(k)是排在Suffix(i-1)前一名的后缀,则它们的最长公共前缀就是h[i-1]。那么Suffix(k+1)将排在Suffix(i)的前面。
若Suffix(k)与Suffix(i-1)的最长公共前缀>=2,Suffix(k)与Suffix(i-1)同时去掉首字符得到Suffix(k+1)与Suffix(i),则Suffix(k+1)排在Suffix(i)的前面,且Suffix(k+1)与Suffix(i)的最长公共前缀=h[i-1]-1。设Suffix(t)是排在Suffix(i)前一名的后缀,则它们的最长公共前缀就是h[i],那么Suffix(t)=Suffix(k+1)或者Suffix(t)排在Suffix(k+1)前面,则h[i]>=h[i-1]-1。
我们可以用后缀数组方便的求LCP,复杂度O(nlog2n)。