DP基础_1 2016.4.29

Make  it  work,   //递归

make  it  right,   //递归

make  it  fast.    //迭代

- kent  beck

一、

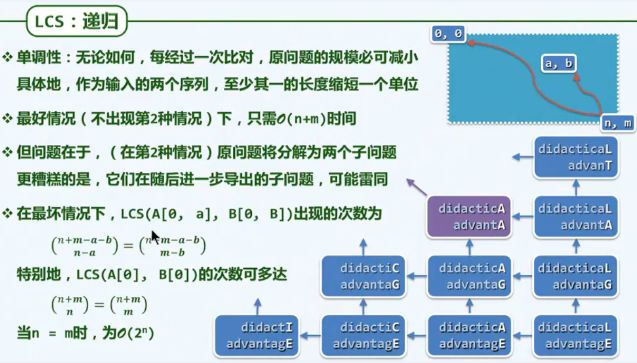
从某种意义上讲，所谓的动态规划(dynamic programming)，也可以理解为：

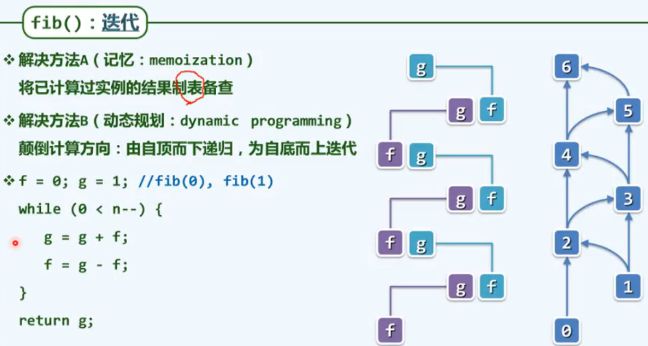
通过递归，找出了算法的本质，并给出了一个初步的解之后，再将其等效地转化为迭代的形式

递归：设计出可行且正确的解

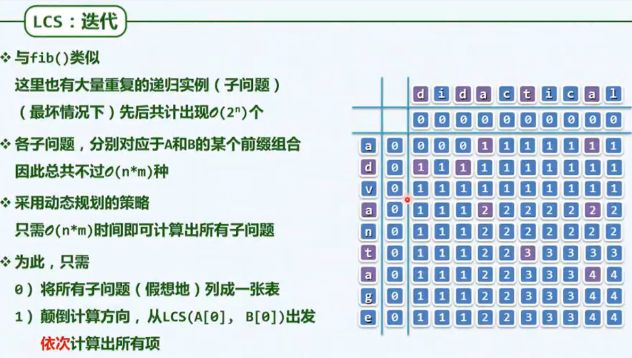
动态规划：消除重复计算，提高效率

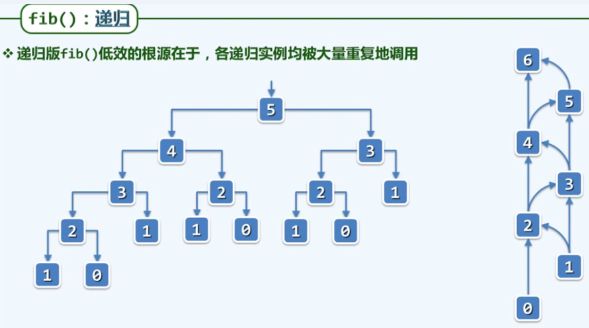
int Fibonacci(int n)    //计算Fibonacci数列的第n项（二分递归版）：O(2^n)  
{  
    if (n < 2) {  
        return n;   //若达到递归基，直接取值  
    } else {  
        return (Fibonacci(n-1) + Fibonacci(n-2));   //否则，递归计算前两项，其和即为正解  
    }  
} 

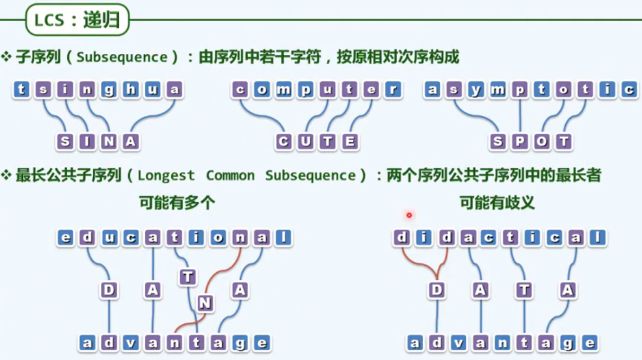
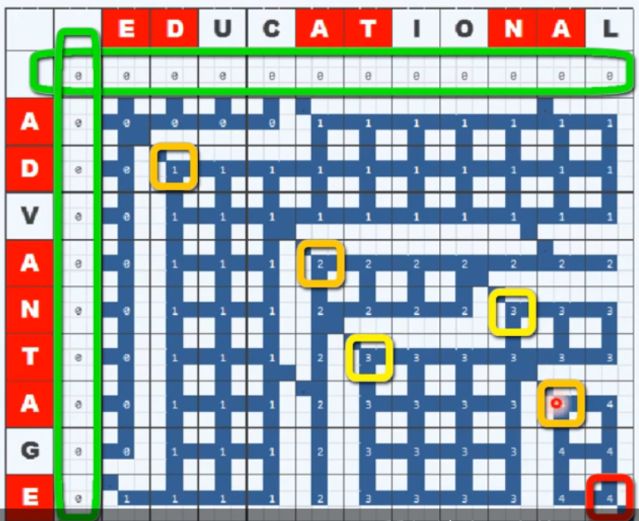
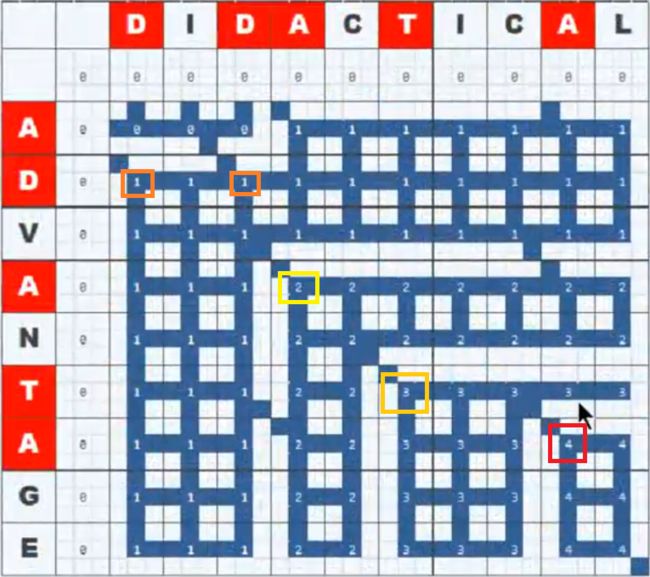
二、最长公共子序列，LCS（Longest Common Subsequence）

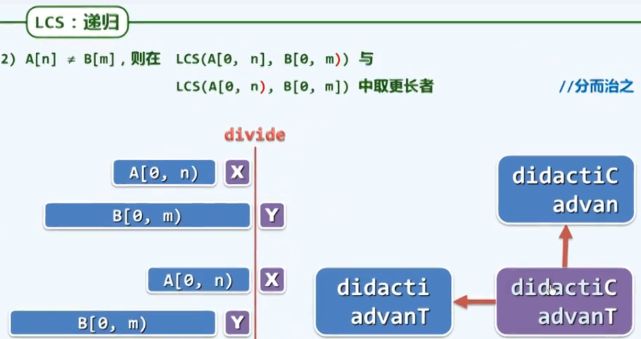
递归

理解

复杂度

动态规划

HDU 1159 Common Subsequence

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int maxn = 1e3;
char X[maxn], Z[maxn];
int G[maxn][maxn];

int LCS(char* a, char* b);

int main()
{
//    freopen("in.txt", "r", stdin);

    while (scanf("%s%s", X, Z) != EOF) {
        printf("%d\n", LCS(X, Z));
    }
    return 0;
}

int LCS(char* a, char* b)
{
    memset(G, 0, sizeof(G));
    int a_len = strlen(a);
    int b_len = strlen(b);
    for (int i=1; i<=a_len; ++i) {
        for (int j=1; j<=b_len; ++j) {
            if (a[i-1] == b[j-1]) {
                G[i][j] = G[i-1][j-1] + 1;
            } else {
                G[i][j] = max(G[i-1][j], G[i][j-1]);
            }
        }
    }
    return G[a_len][b_len];
}

三、最长递增子序列，LIS（ Longest Increase Subsequence）

（1）问题描述

给定 n 个整数 A1,  A2, …,  An，按从左到右的顺序选出尽量多的整数

组成一个递增子序列（子序列可以理解为：删除 0 个或多个数，其他数的顺序不变）

比如，从序列 1,  6,  2, 3,  7,  5 中，可以选出递增子序列 1, 2, 3, 5，也可以选出 1, 6, 7，但前者更长
选出的递增子序列中相邻元素不能相等

（2）转化为LCS求解

设序列（b1, b2, …, bn）是对序列（a1, a2, …, an）按递增排好序的序列

那么它们的最长公共子序列即为（a1, a2, …, an）的最长递增子序列

POJ 2533 Longest Ordered Subsequence

注意：选出的递增子序列中相邻元素不能相等

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>

using namespace std;

const int maxn = 1000 + 10;
int N;
int A[maxn];
int t[maxn];
int G[maxn][maxn];
int Count = 0;
int C_num[maxn];

int LCS(int* a, int* b);
int cmp_num(const void* a, const void* b);

int main()
{
//    freopen("in.txt", "r", stdin);

    while (scanf("%d", &N) != EOF) {
        for (int i=0; i<N; ++i) {
            scanf("%d", &A[i]);
            t[i] = A[i];
        }
        qsort(t, N, sizeof(t[0]), cmp_num);
        printf("%d\n", LCS(A, t));
    }
    return 0;
}

int cmp_num(const void* a, const void* b)
{
    return *(int*)a - *(int*)b;
}

int LCS(int* a, int* b)
{
    memset(G, 0, sizeof(G));
    Count = 0;
    for (int i=1; i<=N; ++i) {
        for (int j=1; j<=N; ++j) {
            if (a[i-1] == b[j-1]) {
                if (Count != 0 && a[i-1] != C_num[Count-1]) {
                    C_num[Count] = a[i-1];
                    G[i][j] = G[i-1][j-1] + 1;
                    ++Count;
                } else if (Count == 0) {
                    C_num[0] = a[i-1];
                    G[i][j] = G[i-1][j-1] + 1;
                    ++Count;
                } else {
                    G[i][j] = max(G[i-1][j], G[i][j-1]);
                }
            } else {
                G[i][j] = max(G[i-1][j], G[i][j-1]);
            }
        }
    }
    return G[N][N];
}

（3）动态规划O(n^2)

设 d(i) 为以 i 结尾的最长递增子序列的长度

则 d(i) = max{0, d(j) | j < i,  Aj < Ai} + 1 = max{1, d(j)+1 | j < i,  Aj < Ai}

最终答案是 max{d(i)}

如果 LIS 中的相邻元素可以相等，把小于号改成小于等于号即可

POJ 2533 Longest Ordered Subsequence

//0MS

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>

using namespace std;

const int maxn = 1000 + 10;
int N;
int A[maxn];
int dp[maxn];

int main()
{
//    freopen("in.txt", "r", stdin);

    while (scanf("%d", &N) != EOF) {
        for (int i=1; i<=N; ++i) {
            scanf("%d", &A[i]);
        }
        for (int i=1; i<=N; ++i) {
            dp[i] = 1;
        }
        for (int i=1; i<=N; ++i) {
            for (int j=1; j<i; ++j) {
                if (A[i] > A[j] && dp[i] < dp[j]+1) {
                    dp[i] = dp[j] + 1;
                }
            }
        }
        int Max = 0;
        for (int i=1; i<=N; ++i) {
            if (dp[i] > Max) {
                Max = dp[i];
            }
        }
        printf("%d\n", Max);
    }
    return 0;
}

（4）动态规划O(nlogn)

考虑构造一个数组B[]

这个数组里放的是已经找到的最优递增序列

那么，我们开始遍历A[i]

如果 A[i] 比数组 B[] 的最大的一个元素（即最后一个元素）还要大，那么就把 A[i] 添加到数组 B[] 的尾部

否则在 B[] 里查找第一个比 A[i] 大的元素，然后将那个元素替换为 A[i] ，保证 B[] 里面的元素是递增的

由于 B[] 里元素是有序的，因此可以用二分查找，就达到了优化的目标

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>

using namespace std;

const int maxn = 1000 + 10;
int N;
int A[maxn];
int B[maxn];

int main()
{
//    freopen("in.txt", "r", stdin);

    while (scanf("%d", &N) != EOF) {
        for (int i=1; i<=N; ++i) {
            scanf("%d", &A[i]);
        }
        B[1] = A[1];
        int Count = 1;
        for (int i=2; i<=N; ++i) {
            if (A[i] > B[Count]) {
                ++Count;
                B[Count] = A[i];
            } else {
                int t = lower_bound(B+1, B+Count+1, A[i]) - B;
                B[t] = A[i];
            }
        }
        printf("%d\n", Count);
    }
    return 0;
}