后缀数组学习
相关学习资料:《后缀数组——处理字符串的有力工具》、《后缀树》(http://wenku.baidu.com/link?url=c5DBWJ9b6UNTzV6uxvQZuPerd4FSOWFWpt8ekWcsgyLXT7LZcy4aKlpI5QZ5fdO8SIGqQDVPlXmIBnbRur0ZWHpmvYTJvmC_r8KWoQ-LWxq)
后缀数组SA: 保存1..n 的某个排列SA[1],SA[2],……,SA[n],并且保证Suffix(SA[i]) < Suffix(SA[i+1]),1≤ i< n
名次数组Rank: 名次数组Rank[i]保存的是Suffix(i)在所有后缀中从小到大排列的“名次”。
先进行字符串的排序,排序的过程有一点像归并排序,从小到大的不断扩展。
盗图一张:
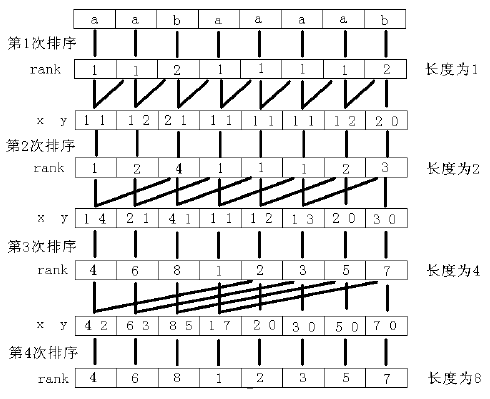
height 数组:定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀。
suffix(j) 和suffix(k) 的最长公共前缀为height[rank[j]+1], height[rank[j]+2], height[rank[j]+3], … ,height[rank[k]]中的最小值。
原串:ababc
拆成后缀组:
0: a b a b c $
1: b a b c $
2: a b c $
3: b c $
4: c $
5: $
对应的排名Rank[]:
0: $
1: a b a b c $
2: a b c $
3: b a b c $
4: b c $
5: c $
假设后缀a排名b,那么我们有:sa[b]=a、Rank[a]=b,它们是互逆的。
在练习中不断熟悉该数据结构。
spoj 694 Distinct Substrings
http://www.spoj.com/problems/DISUBSTR/
大意:给出一个字符串,求出有多少个不同的子串。
分析:第一次使用后缀数组。
假设串的长度是5,那么有这样的统计:
子串长度为1,个数是5
长度是2,个数是4
长度是3,个数是3
长度是4,个数是2
长度是5,个数是1
其中,我们还算了相同的字符子串,height[i]表示排名是i的相邻子串的相同部分的长度,排名第0的是认为加上的$,所以,height[0]=0, height[1]=0。
于是 ans=n(n+1)2−∑i=2nheight[i]
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N=1e3+10;
int t1[N],t2[N],c[N];
bool cmp(int *r,int a,int b,int l){
return r[a]==r[b] && r[a+l]==r[b+l];
}
// sa[i]=value: i是排名 value是下标 rank[i]=value: i是下标 value是排名
// height[i]是suffix(sa[i-1])和suffix(sa[i])的最长公共前缀
void suffix(int str[],int sa[],int Rank[],int height[],int n,int m){
n++; // length+1
int i,j,p,*x=t1,*y=t2; // x[]是原数组 y[]是第二关键排序后的数组
// 第一趟基数排序
for(i=0;i<m;i++) c[i]=0; // c[i]=value: value是排名
for(i=0;i<n;i++) c[x[i]=str[i]]++;
for(i=1;i<m;i++) c[i]+=c[i-1]; //排序完成
for(i=n-1;i>=0;i--) {
sa[c[x[i]]-1]=i;
c[x[i]]--;
}
for(j=1;j<=n;j<<=1){
p=0; //排名数越大优先级越高
for(i=n-j;i<n;i++) y[p++]=i; // 分段后如果字符串的长度小于j 那么排名最低
for(i=0;i<n;i++)
if(sa[i]>=j) y[p++]=sa[i]-j; // 依据sa数组第二关键字排序
// 第一关键字排序
for(i=0;i<m;i++) c[i]=0;
for(i=0;i<n;i++) c[x[y[i]]]++;
for(i=1;i<m;i++) c[i]+=c[i-1];
for(i=n-1;i>=0;i--) sa[--c[x[y[i]]]]=y[i];
swap(x,y); //x --> y
p=1;
x[sa[0]]=0;
for(i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; //x更新排序完成,一次迭代排序搞定
if(p>=n) break;
m=p; // 下次基数排序的最大值
}
int k=0;
n--;
for(i=0;i<=n;i++) Rank[sa[i]]=i;
for(i=0;i<n;i++){
if(k)k--;
j=sa[Rank[i]-1]; // 相似的字符子串 Rank[n]=0
while(str[i+k]==str[j+k]) k++;
height[Rank[i]]=k; //最大相同部分的长度
}
}
char s[N];
int str[N],sa[N],Rank[N],height[N];
int main()
{
//freopen("cin.txt","r",stdin);
int t;
cin>>t;
while(t--){
scanf("%s",s);
int n=strlen(s);
for(int i=0;i<=n;i++){
str[i]=s[i];
}
suffix(str,sa,Rank,height,n,130);
int ans=n*(n+1)/2;
for(int i=2;i<=n;i++){ //Rank=0的是$ 所以height数组是0,0,……
ans-=height[i];
}
printf("%d\n",ans);
}
return 0;
}spoj 705 New Distinct Substrings
http://www.spoj.com/problems/SUBST1/
大意:和Distinct Substring一样求解子串的个数,但是这里的串的长度是5e4。本以为要求将基数排序改成快速排序,我想歪了。。。对于每一个串后缀,假设是第i个,其贡献的串的个数是n-i-height [Rank[i]]
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N=5e4+10;
int t1[N],t2[N],c[N];
bool cmp(int *r,int a,int b,int l){
return r[a]==r[b] && r[a+l]==r[b+l];
}
// sa[i]=value: i是排名 value是下标 rank[i]=value: i是下标 value是排名
// height[i]是suffix(sa[i-1])和suffix(sa[i])的最长公共前缀
void suffix(int str[],int sa[],int Rank[],int height[],int n,int m){
n++; // length+1
int i,j,p,*x=t1,*y=t2; // x[]是原数组 y[]是第二关键排序后的数组
// 第一趟基数排序
for(i=0;i<m;i++) c[i]=0; // c[i]=value: value是排名
for(i=0;i<n;i++) c[x[i]=str[i]]++;
for(i=1;i<m;i++) c[i]+=c[i-1]; //排序完成
for(i=n-1;i>=0;i--) {
sa[c[x[i]]-1]=i;
c[x[i]]--; //start at 0
}
for(j=1;j<=n;j<<=1){
p=0; //排名数越大优先级越高
for(i=n-j;i<n;i++) y[p++]=i; // 分段后如果字符串的长度小于j 那么排名最低
for(i=0;i<n;i++)
if(sa[i]>=j) y[p++]=sa[i]-j; // 依据sa数组第二关键字排序
// 第一关键字排序
for(i=0;i<m;i++) c[i]=0;
for(i=0;i<n;i++) c[x[y[i]]]++;
for(i=1;i<m;i++) c[i]+=c[i-1];
for(i=n-1;i>=0;i--) sa[--c[x[y[i]]]]=y[i];
swap(x,y); //x --> y
p=1;
x[sa[0]]=0;
for(i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; //x更新排序完成,一次迭代排序搞定
if(p>=n) break;
m=p; // 下次基数排序的最大值
}
int k=0;
n--;
for(i=0;i<=n;i++) Rank[sa[i]]=i;
for(i=0;i<n;i++){
if(k)k--;
j=sa[Rank[i]-1]; // 相似的字符子串 Rank[n]=0
while(str[i+k]==str[j+k]) k++;
height[Rank[i]]=k; //最大相同部分的长度
}
}
char s[N];
int str[N],sa[N],Rank[N],height[N];
int main()
{
//freopen("cin.txt","r",stdin);
int t;
cin>>t;
while(t--){
scanf("%s",s);
int n=strlen(s);
for(int i=0;i<=n;i++){
str[i]=s[i];
}
suffix(str,sa,Rank,height,n,130);
int ans=0;
for(int i=0;i<=n;i++){
ans+=n-i-height[Rank[i]];
}
printf("%d\n",ans);
}
return 0;
}————————————————————————————————–
忽然想起来,这份代码既然能A这道题,那么也一定能A掉Distinct Substrings !
poj 2774 Long Long Message
http://poj.org/problem?id=2774
大意:求解两个字符串的最大的连续公共子串长度
分析:这算是另类的最长公共子序列吧!
由于有连续的要求,所以使用后缀数组。height数组存储了排名相邻后缀的最大公共前缀。怎样将子串的分开来呢(两者属于不同的字符串),使用sa数组得到他们的原始排名。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N=2e5+10;
int t1[N],t2[N],c[N];
bool cmp(int *r,int a,int b,int l){
return r[a]==r[b] && r[a+l]==r[b+l];
}
void suffix(int str[],int sa[],int Rank[],int height[],int n,int m){
n++; // length+1
int i,j,p,*x=t1,*y=t2;
for(i=0;i<m;i++) c[i]=0; // c[i]=value: value是排名
for(i=0;i<n;i++) c[x[i]=str[i]]++;
for(i=1;i<m;i++) c[i]+=c[i-1]; //排序完成
for(i=n-1;i>=0;i--) {
sa[c[x[i]]-1]=i;
c[x[i]]--; //start at 0
}
for(j=1;j<=n;j<<=1){
p=0;
for(i=n-j;i<n;i++) y[p++]=i;
for(i=0;i<n;i++)
if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0;i<m;i++) c[i]=0;
for(i=0;i<n;i++) c[x[y[i]]]++;
for(i=1;i<m;i++) c[i]+=c[i-1];
for(i=n-1;i>=0;i--) sa[--c[x[y[i]]]]=y[i];
swap(x,y); //x --> y
p=1;
x[sa[0]]=0;
for(i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
if(p>=n) break;
m=p;
}
int k=0;
n--;
for(i=0;i<=n;i++) Rank[sa[i]]=i;
for(i=0;i<n;i++){
if(k)k--;
j=sa[Rank[i]-1]; // 相似的字符子串 Rank[n]=0
while(str[i+k]==str[j+k]) k++;
height[Rank[i]]=k; //最大相同部分的长度
}
}
char s[N],s2[N];
int str[N],sa[N],Rank[N],height[N];
int main()
{
while(~scanf("%s",s)){
int len1=strlen(s);
scanf("%s",s2);
strcat(s,s2);
for(int i=0;s[i];i++) str[i]=s[i]-'a'+1;
int n=strlen(s);
str[n]=0;
suffix(str,sa,Rank,height,n,30);
int ans=0;
for(int i=2;i<=n;i++){ // sa[i] 排第i的是第几个后缀
if(sa[i-1]>=0 && sa[i-1]<len1 && sa[i]>=len1) ans=max(ans,height[i]);
if(sa[i]>=0 && sa[i]<len1 && sa[i-1]>=len1) ans=max(ans,height[i]);
}
printf("%d\n",ans);
}
return 0;
}poj 3261 Milk Patterns
http://poj.org/problem?id=3261
大意:求解出现次数大于等于k的字符串的最大长度
分析:题目样例的源串是 1 2 3 2 3 2 3 1
那么按照字符串排序后的结果是
1
1 2 3 2 3 2 3 1
2 3 1
2 3 2 3 1
2 3 2 3 2 3 1
3 1
3 2 3 1
3 2 3 2 3 1
由此,相邻串的最长公共前缀长度是
0 1 0 2 4 0 1 3
明白基本原理后,剩下就随意写了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N=1e6+10,M=1e6+5; //N=2e4+10,M=1e6;
int t1[N],t2[N],c[N];
bool cmp(int *r,int a,int b,int l){
return r[a]==r[b] && r[a+l]==r[b+l];
}
// sa[i]=value: i是排名 value是下标 rank[i]=value: i是下标 value是排名
// height[i]是suffix(sa[i-1])和suffix(sa[i])的最长公共前缀
void suffix(int str[],int sa[],int Rank[],int height[],int n,int m){
n++; // length+1
int i,j,p,*x=t1,*y=t2; // x[]是原数组 y[]是第二关键排序后的数组
// 第一趟基数排序
for(i=0;i<m;i++) c[i]=0; // c[i]=value: value是排名
for(i=0;i<n;i++) c[x[i]=str[i]]++;
for(i=1;i<m;i++) c[i]+=c[i-1]; //排序完成
for(i=n-1;i>=0;i--) {
sa[c[x[i]]-1]=i;
c[x[i]]--; //start at 0
}
for(j=1;j<=n;j<<=1){
p=0; //排名数越大优先级越高
for(i=n-j;i<n;i++) y[p++]=i; // 分段后如果字符串的长度小于j 那么排名最低
for(i=0;i<n;i++)
if(sa[i]>=j) y[p++]=sa[i]-j; // 依据sa数组第二关键字排序
// 第一关键字排序
for(i=0;i<m;i++) c[i]=0;
for(i=0;i<n;i++) c[x[y[i]]]++;
for(i=1;i<m;i++) c[i]+=c[i-1];
for(i=n-1;i>=0;i--) sa[--c[x[y[i]]]]=y[i];
swap(x,y); //x --> y
p=1;
x[sa[0]]=0;
for(i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; //x更新排序完成,一次迭代排序搞定
if(p>=n) break;
m=p; // 下次基数排序的最大值
}
int k=0;
n--;
for(i=0;i<=n;i++) Rank[sa[i]]=i;
for(i=0;i<n;i++){
if(k)k--;
j=sa[Rank[i]-1]; // 相似的字符子串 Rank[n]=0
while(str[i+k]==str[j+k]) k++;
height[Rank[i]]=k; //最大相同部分的长度
}
}
int str[N],sa[N],Rank[N],height[N];
int main()
{
//freopen("cin.txt","r",stdin);
int n,k;
while(~scanf("%d%d",&n,&k)){
for(int i=0;i<n;i++) {
scanf("%d",&str[i]);
str[i]++;
}
str[n]=0; // 不能设成-1,算法中有c[x[i]=str[i]]++;
//str[n]=-1;
suffix(str,sa,Rank,height,n,M);
int ans=0;
//for(int i=0;i<=n;i++) cout<<height[i]<<" "; cout<<endl;
for(int i=1;i<=n;i++){
int minm=height[i];
for(int j=i;j<=n;j++){
minm=minm<height[j]?minm:height[j];
if(j-i+2>=k) ans=ans>minm?ans:minm;
if(minm<ans) break;
}
}
printf("%d\n",ans);
}
return 0;
}