数据结构与算法7: 二叉搜索树基本操作（Binary search tree basic operation )

写在前面
二叉树是应用广泛的一类树，通过学习二叉搜索树（BST）、平衡二叉树(AVL)、伸展树(Splay Tree)以及二叉堆(Binary Heap)的相关概念、操作以及分析算法性能，对理解树有很大帮助。本节总结二叉搜索树(BST)的基本概念和操作，包括查找、插入和删除。建议时间充足的初学者，自己动手全部实现一遍代码，必定会获得很大的收益。笔者在此过程中获益良多，注意思考:

• 递归与非递归实现转换
• 复制删除和合并删除两种方法的特点

1定义

二叉搜索树(Binary Search Tree):二叉查找树，也称二叉搜索树、有序二叉树（ordered binary tree），排序二叉树（sorted binary tree）。它或者是一棵空树；或者是指具有如下性质的二叉树:

(1)若它的左子树不为空，则左子树上所有的节点的值均小于它的根节点的值 (2) 若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值(3) 它的左、右子树也分别为二叉搜索树。

在实现的过程中，我们为了便于与后面的AVL、SplayTree统一; 同时也为了保持注意力在数据结构而不是c++程序设计，这里未使用泛型编程，只处理整数类型，因此定义节点结构为:

class BSTNode {
public:
   BSTNode(const int& e,BSTNode*p ,BSTNode *l=0,BSTNode *r=0)
   :key(e),height(1) ,parent(p),left(l),right(r){
          }
   std::string toString() const{    // 用于调试
        std::ostringstream oss;
        oss << key;
        return oss.str();
   }
private:
          int key;
          int height; // 以这个结点为根的树的高度
          BSTNode *parent,*left,*right;
          friend class BST;  // 二叉搜索树
          friend class AVLTree; // 平衡二叉树
          friend class DSWTree; // DSW算法实现的BST
          friend class SplayTree; // 伸展树
          friend class BiTreePrinter; // 将BST转换为图片的类
};

实际实现的过程中，笔者也体会到:
为节点增加两个域：height和parent，与没有这两个域的代码相比，显得更难维护，因为任何操作结束后必须维护height和parent这两个域。但是为了统一实现，我们还是增加了这两个域，这样做的好处是代码得到很好的复用。
编写的二叉搜索树类间关系如下图所示:

2 查找

查找操作是一个基本操作，在插入和删除的过程中都要定位待处理的节点在树中的位置。算法思想很简单，实现如下。

迭代实现:

/** * 查找操作 * 非递归实现 * 找到则返回包含键的结点指针，prev键的父节点 * 否则返回0,prev指向待插入位置的父节点 */
BSTNode* BST::iterativeSearch(const int& e,BSTNode*&prev) {
    BSTNode* current = root;
    prev = 0;
    while(current != 0 && e != current->key) {
      prev = current;
     if(e < current->key)
        current = current->left;
     else
       current = current->right;
    }
    return current;
} 

递归实现如下:

/** * 查找操作 * 递归实现 */
BSTNode* BST::recursiveSearch(BSTNode* p, const int& e) {
        if(p == 0 || e == p->key)
            return p;
        else if(e < p->key)
            return recursiveSearch(p->left,e);
        else
            return recursiveSearch(p->right,e);
}

3 插入

二叉树的插入主要思想:
插入元素e从根节点开始逐一比较，直至找到该元素或者找到该元素的插入位置时停止。比较过程中有三种情况:

case 1: e如果比当前节点大，则与当前节点的右孩子的根节点比较,即当前节点右孩子设为当前节点，继续比较；
case 2: e如果比当前节点小，则与当前节点的左孩子的根节点比较,即当前节点左孩子设为当前节点，继续比较；
case 3: e如果与当前节点相等，则不插入。

重复这个过程，直到当前节点为空时，这个位置即为插入的位置。

插入算法比较简单，迭代实现如下所示:

/** * 插入元素 * 迭代实现 * 如果键值已经存在则返回false * 否则插入成功返回true,插入错误返回false * 算法： * 1)首先通过比较值的大小，查找插入位置 * 2)在插入位置处添加新结点 * 3)更新插入结点路径上的结点的高度值 */
bool BST::insert(const int& e){
        BSTNode *prev = 0;  // prev 保存插入点的父节点
        BSTNode *current =iterativeSearch(e,prev)
        if(current != 0)
            return false;
        if(prev == 0)
            root = new BSTNode(e,prev);
        else if(e < prev->key)
            prev->left = new BSTNode(e,prev);
        else
            prev->right = new BSTNode(e,prev);
        insertAdjust(prev,e);   // 自底向上调整结点的高度值
        return true;
}

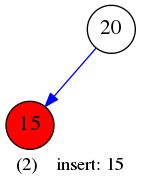
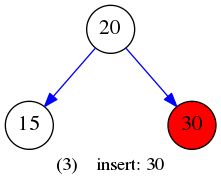
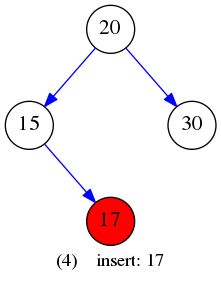
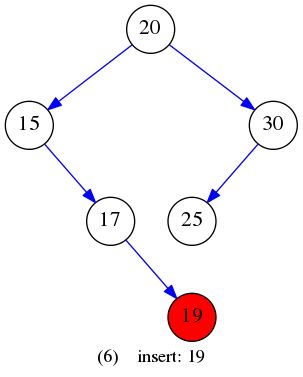
给定数据:
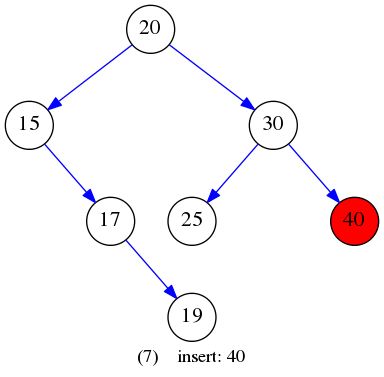
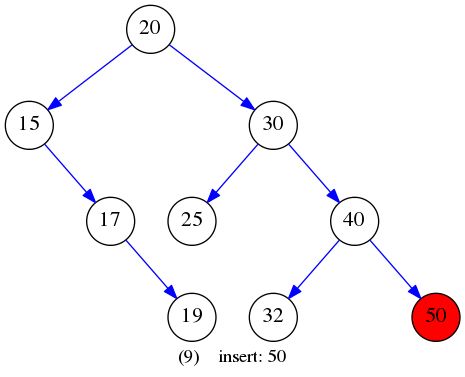
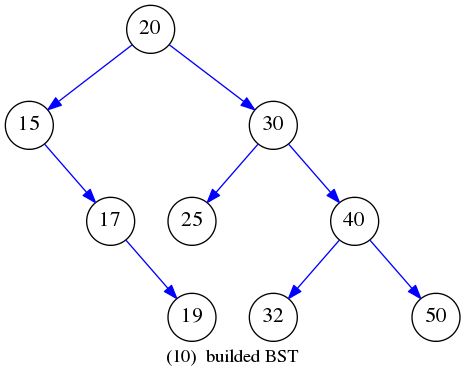
int insertEle[] = {20,15,30,17,25,19,40,32,50};
插入元素构建BST的过程如下图所示:

4 删除

4.1 复制删除(remove by copy)

复制删除的基本思想：
当BST中删除某个节点p时，删除后必须仍然满足定义中的约束，因此需要分三种情况处理:

case 1: 对于没有孩子的结点，直接删除即可
case 2: 对于只有一个孩子的结点，直接把孩子替换待删除结点即可
case 3: 对于两个孩子都不为空的结点p，复制的思想即为：
寻找p的前驱节点(后继节点也可以，是一个对称的操作)，将前驱节点的值复制到p中，然后删除这个前驱节点(前驱节点就是p的左子树根节点的最右边孩子结点，这个前驱节点最多只有一个孩子，因此转换为case1和case2的情况)。

对于case3,例如3中的二叉树，删除20时，前驱结点是19，将前驱键值19复制到20对应节点，然后再删除19这个结点即可(实际删除节点为前驱19，而不是结点20)。对应过程如下图所示:

代码实现:

/** * 复制删除指针p指向结点 * 算法思想： * case 1: 对于没有孩子的结点，直接删除即可 * case 2: 对于只有一个孩子的结点，直接把孩子替换待删除结点即可 * case 3: 对于两个孩子都不为空的结点 * 首先找p左孩子的最右边结点tmp,tmp结点即为要复制的那个结点 * 如果p的左孩子没有右孩子，将p的左孩子的左孩子链接到p的left上 * 否则将tmp的左孩子链接到其父节点right上 * 将tmp值复制到p中 * 最后释放结点,并调整结点的高度值 */
void BST::removeByCopying(BSTNode*& p,const int& e){
    BSTNode* tmp = p,*prev=p->parent;       // prev指针指向实际删除结点的父节点
    if(p->left == 0)        {           // 左子树为空
        if(p->right != 0)
            p->right->parent = p->parent;
        p = p->right;
    }
    else if(p->right == 0) {            // 右子树为空
        if(p->left != 0)
            p->left->parent = p->parent;
        p = p->left;
    }
    else {
        prev = p;   // prev初始为指向待删除结点
        tmp = p->left;
        while(tmp->right != 0) {
            prev = tmp;
            tmp = tmp->right;
        }
        if(prev == p)   // p的左孩子没有右孩子
            prev->left = tmp->left;
        else
            prev->right = tmp->left; // tmp有左孩子则连上，没有也用tmp->left将其父节点right置为空
        if(tmp->left != 0)
            tmp->left->parent = prev;
        p->key = tmp->key;
    }
    delete tmp;
    removeAdjust(prev,e);   // 自底向上更新结点的高度值
}

4.2 合并删除(remove by merging)

合并删除的思想，与复制删除的不同之处主要体现在case3的处理上。
case3时，合并删除，将删除节点p的右子树重新合并到前驱的右子树上(前驱节点也即p的左子树根节点的最右边孩子结点，它无右孩子，因此将p的右子树合并到这个前驱结点的右子树上)，结点p的左孩子的根成为新的根结点(将p的左子树链接到p的后继的左子树上，是一个对称的操作，这种方法也是可以的)。

例如3图中的二叉树，删除20时，前驱节点是19,将右子树连接到19上，将15重新设定为根节点，过程如下图所示:

合并为:

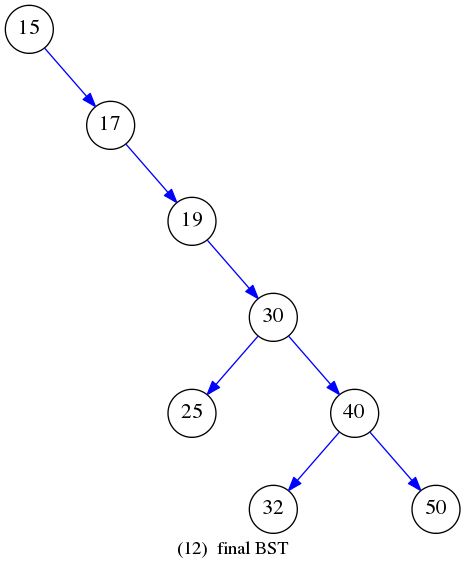
代码实现为:

/** * 合并删除指针p指向结点 * 算法思想： * case 1:对于没有孩子的结点，直接删除即可； * case 2: 对于只有一个孩子的结点，直接把孩子替换待删除结点即可 * case 3:对于有两个孩子的结点，将右孩子挂在左孩子树上最右边孩子结点的右指针上 * 最后释放结点,并调整结点的高度值 */
void BST::removeByMerging(BSTNode*& p,const int&e){
    BSTNode *  tmp = p,*prev=p->parent; // tmp保存待释放内存地址 prev结点保存待调整的结点
    if(p->left == 0)        {  // 左子树为空
        if(p->right != 0)
            p->right->parent = p->parent;
        p = p->right;
    }
    else if(p->right == 0) { // 右子树为空
        if(p->left != 0)
            p->left->parent = p->parent;
        p = p->left;
    }
    else {
        tmp = p->left;
        while(tmp->right != 0)// tmp 临时指向p左孩子中最右边孩子
             tmp = tmp->right;
        prev = tmp;
        tmp->right = p->right;
        p->right->parent = tmp;
        p->left->parent = p->parent;
        tmp = p;    // tmp 重新指向待释放结点
        p = p->left;
    }
    delete tmp;
    removeAdjust(prev,e);   // 自底向上更新结点的高度值
}

删除时注意：
(1)删除时首先要通过搜索找到待删除节点,这个可以通过iterativeSearch函数实现。
(2)删除时我们使用的函数原型为:

    void removeByMerging(BSTNode*& p,const int& e);
    void removeByCopying(BSTNode*& p,const int& e);

这里可以从待删除节点p的上层传递引用，例如p是上层节点的左孩子则传递为p->parent->left,在函数中重新将p->parent->left指定为新的节点。当然也可以不使用引用，而是直接在函数中进行判断。这取决于你怎么实现。
将(1)(2)合并后，我们实现为两个函数:

bool findAndRemoveByMerging(const int& e);
bool findAndRemoveByCopying(const int& e);

将这两个函数作为接口提供给外部使用，而这两个函数分别调用对应的removeByxxx版本。例如findAndRemoveByCopying实现为:

/** * 复制删除键值为e的结点 * 删除成功返回true,键值不存在时删除失败返回false */
bool BST::findAndRemoveByCopying(const int& e){
    BSTNode *prev = 0;
    BSTNode *current =iterativeSearch(e,prev);
    if(current == 0)
        return false;
    if(prev == 0)
        removeByCopying(root,e);
    else if(current == prev->left)
        removeByCopying(prev->left,e);
    else
        removeByCopying(prev->right,e);
    return true;
}

findAndRemoveByMerging有类似实现。
另外，无论是插入还是删除之后，为了维护结点的height域，必须进行更新，因此需要调用insertAdjust或者removeAdjust这两个函数，在BST中只需要简单的更新节点的高度即可。后面，我们将会看到，在AVL树或者是SplayTree中，为了保持树的平衡或者为了调整常用节点到根节点，这两个函数的实现各有不同。因此，在基类BST中，我们将其声明为虚函数，并提供了一个默认实现，即只调处理节点及其上层结点的高度值。

virtual void insertAdjust(BSTNode* p,const int&e);// 子类按需实现
virtual void removeAdjust(BSTNode* p,const int&e);// 子类按需实现

在基类BST中，这两个函数的实现相同，我们将其实现为:

/** * 插入结点后调整动作 * 从节点current自底向上调整结点的高度 * 直到一个节点在插入e前后其高度值不变 或者 直到更新完根节点停止 */
void BST::insertAdjust(BSTNode* current,const int&e) {
    while(current != 0) {
        if(current->height == calcHeight(current))
                break;// 插入e前后高度值没变，则上层结点无需调整
        current->height = calcHeight(current);
        current = current->parent;
    }
}
/** * 删除结点后调整动作 * 从节点current自底向上调整结点的高度 */
void BST::removeAdjust(BSTNode* current,const int&e) {
    insertAdjust(current,e);// 默认与插入后调整动作相同
}

其中calcHeight函数根据节点的左右孩子计算其高度。实现如下：

/** * 获取结点p的高度 * 比较p孩子节点高度，取两者最大者加1 */
int BST::calcHeight(const BSTNode* p) const{
    if(p == 0) return 0;
    if(p->left == 0 && p->right == 0)
        return 1;
    else if(p->left == 0)
        return p->right->height+1;
    else if(p->right == 0)
        return p->left->height+1;
    else
        return std::max(p->left->height,p->right->height)+1;
}

关于二叉搜索树的遍历，请参见下一篇内容。