线段树的基本操作
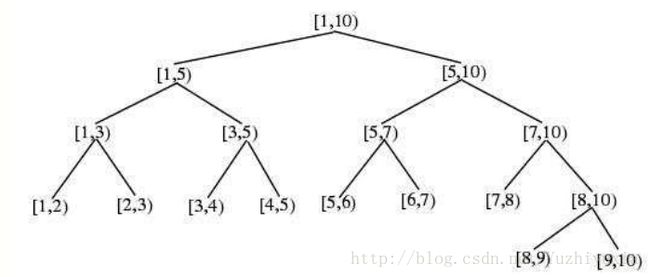
线段树:线段树是一种平衡二叉查找树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。主要的处理思想是基于分治的思想。它的逻辑结构如下:
设根节点的区间为[a,b),区间长度为L = b - a,线段树的性质:
(1)线段树是一个平衡树,树的高度为log(L)
(2)线段树把区间上的任意长度为L的线段都分成不超过2log(L)线段的并
线段树基础存储结构如下:(这里使用数组模拟指针,类似堆的存储结构)
typedef struct{<pre name="code" class="cpp"> int left,right;
int cover, mid;
}TreeNode;创建线段树
void BuildLineSegTree(int left,int right,int nodeNum)
{
node[nodeNum].left = left;
node[nodeNum].right = right;
node[nodeNum].mid = left + (right - left) / 2;
node[nodeNum].cover = 0;
//判断是否是叶子节点
if(left != right-1)
{
BuildLineSegTree(left,node[nodeNum].mid,2 * nodeNum);
BuildLineSegTree(node[nodeNum].mid,right,2 * nodeNum + 1);
}
}
插入线段树
void InsertLineSegTree(int left,int right,int nodeNum)
{
//判断区间是否完全覆盖
if(node[nodeNum].left == left && node[nodeNum].right == right)
{
node[nodeNum].cover += 1;
return ;
}
if(right <= node[nodeNum].mid)
{
//线段在左子树上
return InsertLineSegTree(left,right,2*nodeNum);
}
else if(left >= node[nodeNum].mid)
{
//线段在右子树上
return InsertLineSegTree(left,right,2 * nodeNum + 1);
}
else
{
//线段一部分在左子树上,一部分在右子树上
return InsertLineSegTree(left,node[nodeNum].mid,2*nodeNum)||InsertLineSegTree(node[nodeNum].mid,right,2*nodeNum + 1);
}
}
查询线段树
int SearchLineSegTree(int left,int right,int nodeNum)
{
if(node[nodeNum].left == left && node[nodeNum].right == right)
{
//线段完全覆盖,若该线段存在则返回1,否则返回0
return node[nodeNum].cover;
}
if(right <= node[nodeNum].mid)
{
//线段在左子树
return SearchLineSegTree(left,right,2 * nodeNum);
}
else if(left >= node[nodeNum].mid)
{
//线段在右子树
return SearchLineSegTree(left,right,2 * nodeNum + 1);
}
else
{
//线段一部分在左子树,一部分在右子树
return SearchLineSegTree(left,node[nodeNum].mid,2*nodeNum)&&SearchLineSegTree(node[nodeNum].mid,right,2*nodeNum + 1);
}
}
删除线段树
int DeleteLineSegTree(int left,int right,int nodeNum)
{
if(node[nodeNum].left == left && node[nodeNum].right == right)
{
//线段完全覆盖,若该线段存在则返回1,否则返回0
int ret = node[nodeNum].cover;
node[nodeNum].cover = node[nodeNum].cover > 0 ? node[nodeNum].cover - 1 : 0;
return ret;
}
if(right <= node[nodeNum].mid)
{
//线段在左子树
return DeleteLineSegTree(left,right,2 * nodeNum);
}
else if(left >= node[nodeNum].mid)
{
//线段在右子树
return DeleteLineSegTree(left,right,2 * nodeNum + 1);
}
else
{
//线段一部分在左子树,一部分在右子树
return DeleteLineSegTree(left,node[nodeNum].mid,2*nodeNum)&&DeleteLineSegTree(node[nodeNum].mid,right,2*nodeNum + 1);
}
}