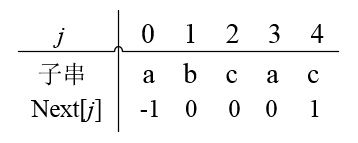【数据结构】KMP算法

1.传统模式匹配算法

       子串的定位操作通常称为串的模式匹配，即输入字符串S（主串）、字符串T（子串）及一个整型pos（0≤pos≤字符串S的长度），返回子串T在主串S中第pos个字符之后的位置，其中T称为模式串。

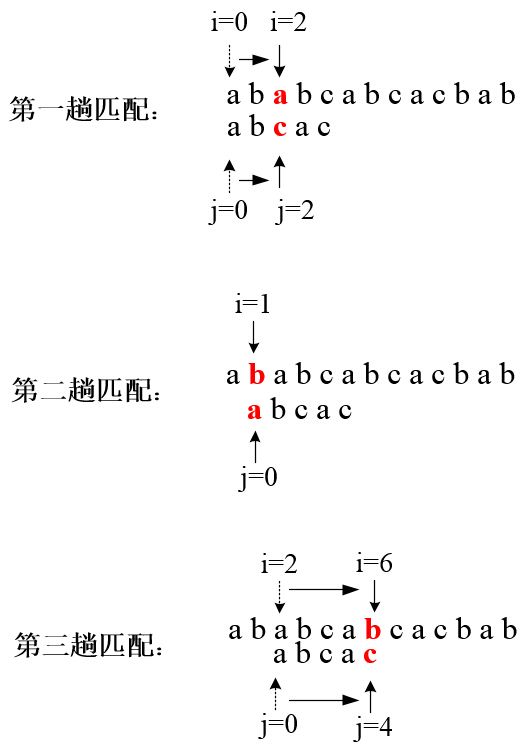
        以S="ababcabcacbab "，T="abcac "，pos=0为例，传统的串的模式匹配算法基本思想是：从主串S的下标为pos（注意：本文中字符串下标默认从0开始！）的字符起和模式T的第一个字符比较，若相等，则继续逐个比较后续字符；否则从主串的下一个字符起再重新和模式T的字符比较之。

        具体过程如下：

       

                           

       

       这种算法在最坏情况下的时间复杂度为O(m*n)，即每次比较到模式T的最后一个字符才发现不匹配。

2.KMP算法

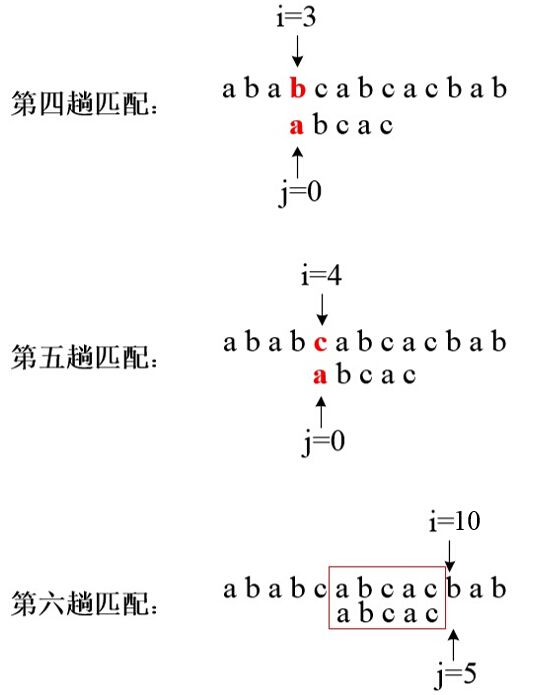
       KMP算法是一种改进的模式匹配算法，它可以在O(n+m)的时间数量级上完成串的模式匹配操作。其改进在于：每当一趟匹配过程中出现字符比较不等时，不需要回溯 i指针，而是利用已经得到的“部分匹配“结果，将模式T向右滑动尽可能远的一段距离后，继续进行比较。具体过程如下：

       

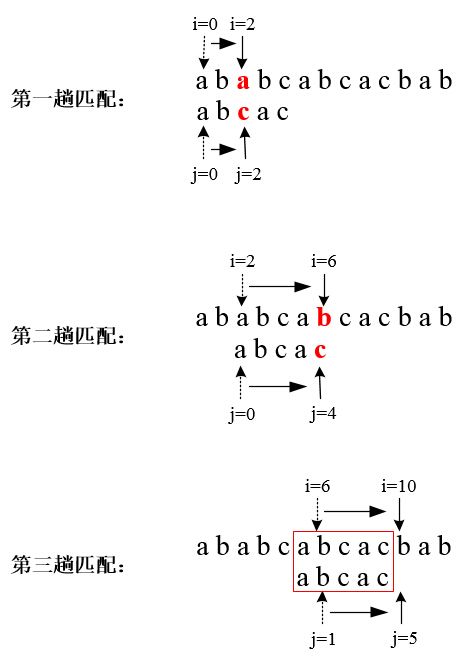
        使用KMP算法，仅通过3次匹配就可以找到所示例子中子串在主串中的位置，而传统方法需要6次匹配。由上面的过程可以发现：a.指向主串的指针i 在字符不匹配时不需要回溯；b.匹配不再从子串的第一个字符开始，例如第三趟比配，子串从下标为 1 的字符开始与主串下标为 6的字符开始进行比较，因为子串下标为0的字符已经与主串下标为5的字符相匹配了。也就是说，KMP不回溯主串指针 i，仅回溯子串指针 j ，将 j 回溯到使其所指字符前面所有字符与 i 所指字符前面字符对应相匹配的位置。因此，KMP算法需要解决的问题是确定当字符不匹配时，指向子串的指针j 应该回溯到哪个位置。

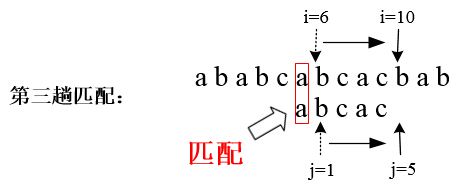
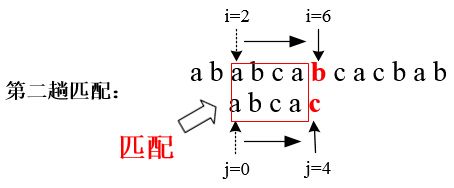
       假设此时指向子串的指针 j 应该与回溯到下标为k (k<j)的位置，意味着子串中下标为 K 的字符前面下标为0 到 K-1 的前 K 个字符与主串中下标为 i 的字符前面下标为i-k 到 i-1的 K 个字符对应相等。例如：上述例子中的第三趟匹配，j回溯到 k=1 位置，则j回溯后，i、j所指字符前面1个（j=1）字符是匹配的，如下图所示：

      

      上述说明转换成公式，即有：           "T0T1...Tk-1"="Si-kSi-k+1...Si-1"                          （1）

      此时，子串中下标为 j的字符与主串中下标为 i 的字符比较时不相等，则说明子串中下标为 j 的字符前面下标为0 到 j-1的前 j 个字符与主串中下标为i 的字符前面下标为 i-j 到i-1 的 j 个字符是已经匹配的。例如：上述例子中的第二趟匹配，主串中下标为i=6的字符与子串中下标为j=4的字符比较不相等，则i、j所指字符前面4个（j=4）字符是匹配的，如下图所示：

      

       即有： "T0T2...Tj-1"="Si-jSi-j+1...Si-1" 。因为 k<j , 既然 i、j 所指字符前面 j 个字符都匹配，自然可以得到 i、j 所指字符前面k 个字符也匹配，即得到“部分匹配结果”：   

                                                          "Tj-kTj-k+1...Tj-1"="Si-kSi-k+1...Si-1"                   （2）
        由（1）（2）可得：                 

                                                            "T0T1...Tk-1"="Tj-kTj-k+1...Tj-1"                        （3）

        由（3）可以得知，当子串中下标为 j 的字符与主串下标为 i的字符不匹配时，j 需要回溯到下标为 k 的位置，k满足的条件是：子串下标为 j 的字符前面k 个字符构成的子串 = 子串前 k个字符构成的子串。例如：前面所给的例子中，T[4]与S[6]不匹配时，j 回溯到 k=1 位置，因为子串T[6]的前1个字符与子串前1个字符相等，即T[5]=T[0]。

       若另 next [ j ]  = k，next[j ] 表示子串中下标为j的字符与主串中相应字符不匹配时，子串中应该重新与主串中该字符进行比较的字符的下标。由上可以得到next[j ]的计算公式如下：
       

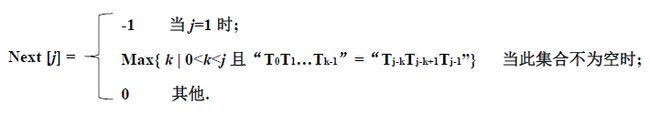
        由该公式得到上述例子中T="abcac"的next数组如下：

        

        给出一个新例子，T=“abaabcac"的next数组为：

       

        next数组求解的代码如下：

int* GetNext(string s)
{
    int* next=new int[s.size()];
    next[0]=-1;
    for(int j=1;j<s.size();j++)
    {
        int tempK=0;
        for(int k=1;k<j;k++)//1<k<j
        {
            int i=0;
            while(i<k&&s[i]==s[j-k+i])
                i++;
            if(i==k&&k>tempK)
                tempK=k;
        }
        next[j]=tempK;
    }
    return next;
}

      由上面分分析可以得到KMP算法如下：

      1.获得子串T的next数组；

      2.使指针 i 指向主串 S 的下标为 pos 的字符，j指向子串 T 的第一个字符；

      3.若S[i]=T[j]，i、j均向右挪动一位；

         若S[i]≠T[j]，且next [j] = -1，则说明子串的第一个字符就匹配不成功，将主串的指针i 向右挪动一位;

         若S[i]≠T[j]，且nex t[j] ≠ -1，将子串的指针的指针 j回溯到 next[j]的位置；

      4.重复步骤3，直至主串或者子串扫描到结尾处；

      5.若子串扫描到结尾处，则匹配成功，返回子串在主串中的起始位置；否则匹配失败，返回-1。

     

       KMP算法代码如下：

int KMP(string S,string T,int pos)  //KMP算法求子串T在主串pos下标字符之后的位置
{
    int* next=GetNext(T);           //获得子串的next数组
    int i=pos,j=0;                  //主串从下标为pos的字符开始进行匹配，子串从第一个字符开始匹配
    while(i<S.size()&&j<T.size())
    {
        if(S[i]==T[j])              //若对应字符相匹配，主串和子串指针向右挪动一位
        {
            i++;
            j++;
        }
        else if(next[j]==-1)        //若对应字符相不匹配，且为子串的第一个字符，主串指针向右挪动一位
            i++;
        else
            j=next[j];              //若对应字符相不匹配，且为不为子串的第一个字符，子串指针回退到next[j]位置
    }
    if(j==T.size())                 //若子串扫描完毕，说明匹配成功，返回起始位置
        return i-T.size();
    else                            //匹配失败，返回-1
        return -1;
}

后话：

         可能编辑的时候有些打错的地方，或者画图或是理解也有错误的地方，欢迎批评指正！

         我写的算法可能与有些地方写的不一样，但是原理都是一样的。比如，我一般会基于代码实现来讲解，因此我前面说明数组下标从0开始，而很多地方的KMP算法讲解都是默认数组下标从1开始的。

         画图真是蛮辛苦也蛮费时间的，只是希望给一些算法初学者，或者代码初学者一些小小的帮助~~谢谢观赏~

         email: [email protected]