R语言与Markov Chain Monte Carlo(MCMC)方法学习笔记(1)
蒙特卡洛方法被誉为20世纪最伟大的十大算法之一。它由美国拉斯阿莫斯国家实验室的三位科学家John von Neumann, Stan Ulam 和 Nick Metropolis于1946年提出。
蒙特卡洛算法之所以那么有名,我的理解就是它利用随机模拟给出了一个十分普遍的求解许多问题近似解的办法。一个十分形象的例子是:在广场上画一个边长一米的正方形,在正方形内部随意用粉笔画一个不规则的形状,现在要计算这个不规则图形的面积,怎么计算?蒙特卡洛(Monte Carlo)方法告诉我们,均匀的向该正方形内撒N(N 是一个很大的自然数)个黄豆,随后数数有多少个黄豆在这个不规则几何形状内部,比如说有M个,那么,这个奇怪形状的面积便近似于M/N,N越大,算出来的值便越精确。在这里我们要假定豆子都在一个平面上,相互之间没有重叠。(撒黄豆只是一个比喻。)我们在《R语言与分类算法的绩效评估》一文计算AUC时用的就是这个方法。
要说道Monte Carlo模拟,那么我们就得从随机数的产生开始说。
一、常见的抽样方法
常见的抽样方法有许多,如直接抽样法(逆变换法)、拒绝抽样法、重要抽样法等。由于逆变换法过于简单,我们在这里就不再讨论了,我们先来看看拒绝抽样。
接受-拒绝抽样(Acceptance-Rejectionsampling)
拒绝抽样的算法也十分简单,我们之所以会花一定的篇幅介绍它,是因为它是MCMC方法的一个基础。拒绝抽样的基本思想是,我们需要对一个分布f(x)进行采样,但是却很难直接进行采样,所以我们想通过另外一个容易采样的分布g(x)的样本,用某种机制去除掉一些样本,从而使得剩下的样本就是来自与所求分布f(x)的样本。
它有几个条件:1)对于任何一个x,有f(x)<=M*g(x);也就是说我们的初步采样是必须包括进一步取样的全体的 2) g(x)容易采样;3) g(x)最好在形状上比较接近f(x)。当然,这样拒绝的概率会小很多,我们可以通过接下来的例子说明。
具体的采样过程如下:
- 对于g(x)进行采样得到一个样本xi, xi ~ g(x);
- 对于均匀分布采样 ui ~ U(a,b);
- 如果ui<= f(x)/[M*g(x)], 那么认为xi是有效的样本;否则舍弃该样本; (# 这个步骤充分体现了这个方法的名字:接受-拒绝)
- 反复重复步骤1~3,直到所需样本达到要求为止。
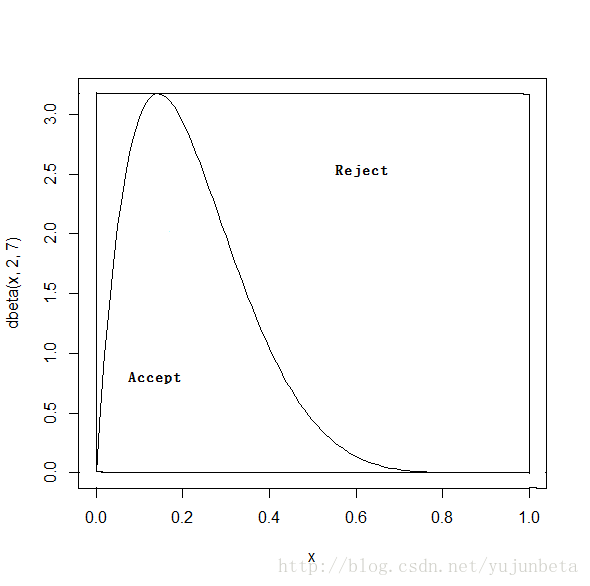
例:我们要产生服从beta(2,7)的随机数。一个简单的办法就是将g取为均匀分布,常数M取为beta(2,7)的密度函数的最大值。显然这是满足拒绝抽样的几个条件。
对应的R代码给出如下:
a<-2 b<-7 xmax<-(a-1)/(a+b-2) dmax<-xmax^(a-1)*(1-xmax)^(b-1)*gamma(a+b)/(gamma(a)*gamma(b)) y<-runif(1000) x<-na.omit(ifelse(runif(1000)<=dbeta(y,a,b)/dmax,y,NA))
我们可以看看KS检验报告的结果:
> z<-x[1:323]
> ks.test(z,"pbeta",2,7)
One-sampleKolmogorov-Smirnov test
data: z
D = 0.0317, p-value = 0.9026
alternative hypothesis: two-sided
可见的确是生成了分布为beta(2,7)的随机数。我们可以用图来说明这个办法:
可见g(x)如果与f(x)的形状相差较大时,效率是比较低的,本次运行的接受概率仅有0.323而已。
利用马氏链的接受-拒绝抽样(Acceptance/rejectionMethod using a Markov Chain)
离散时间的马氏链是许多类随机数(有离散的也有连续的,有一元的也有多元的)生成办法的基础。不同的利用马氏链的生成随机数的办法的不同之处在于转移核的不同。某些时候,转移核包含了拒绝/接受的决定(也就是前面算法的步骤3)。通过这样的拒绝/接受的选择,可以得到一条新的马氏链,使得新链的平稳分布是我们希望的分布。这种利用马氏链来生成样本的模拟办法就是大名鼎鼎的MCMC算法。
MCMC算法虽然简单,但是要用好它却十分的不易。我们先来介绍如何利用MCMC方法来生成随机数。
这个算法通常被称为Metropolis算法,是蒙特卡洛方法中最著名的算法。1953年,Nicolas Metropolis连同Arianna W. Rosenbluth、 Marshall N. Rosenbluth 、Augusta H. Teller、 EdwardTeller在《The Journal of Chemical Physics》上发表了一篇题为“Equationsof State Calculations by Fast Computing Machines”的文章,提出了后来以NicolasMetropolis的名字命名的算法。这篇文章至今已被引用了17 000多次。
我们将想法大致描述一下:对于有密度p的分布,我们可以利用随机游走与p在随机游走当前步的取值来构造接受/拒绝抽样。一种最简单的办法是:对于当前步y(i),我们可以通过随机游走走到下一步y(i+1)=y(i)+s,s是-a到a上的均匀分布,且在p(y(i+1))/p(y(i))>u时接受y(i+1)。(u是0到1上的均匀分布)。如果分布的取值范围是有限的,那么随机游走是不允许走出这个范围的。
我们将这个想法具体描述如下:
例(续):我们尝试用这样的办法来生成beta(2,7)。我们不妨将初始点确定为0.1,s视为服从U(-0.2,0.2)的随机数。
R代码给出如下:
N <- 3000 #抽样个数
x <- c()
x0 <- 0.1 # 初始值
x[1] <- x0
k <- 0 #k表示拒绝转移的次数
u <- runif(N) #抽取均匀分布随机数
for (i in 2:N) {
y <- x[i-1]+runif(1,-0.2,0.2)
if(0<y&y<1){
if (u[i] <=(dbeta(y,2,7)/dbeta(x[i-1],2,7)))
x[i] <- y
else {
x[i]<- x[i-1]
k <-k + 1
}
}
else
x[i]<-x0
}
这里有几点是值得关注的:
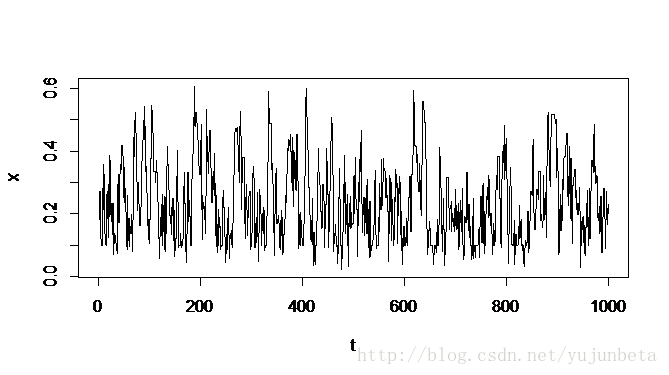
- 这里得到的x是高度自相关的,要得到我们希望的分布,需要对x进行采样,采样的步长视自相关系数而定,在本例中大致为30。
- 我们通常需要判断x是否达到了一个平稳分布,做出x的样本路径对于判断x是十分有助益的。
- 我们这里将x越界粗暴的处理为回到初始点,或者后退为上一步取值不是不行,但一个更好地办法就是重新参数化,这样的效率更高,效果也更好。
我们可以来看看x的样本路径:
可以看出x是稳定的,没有漂移的情况发生。我们可以认为这个马氏链的构造是成功的。
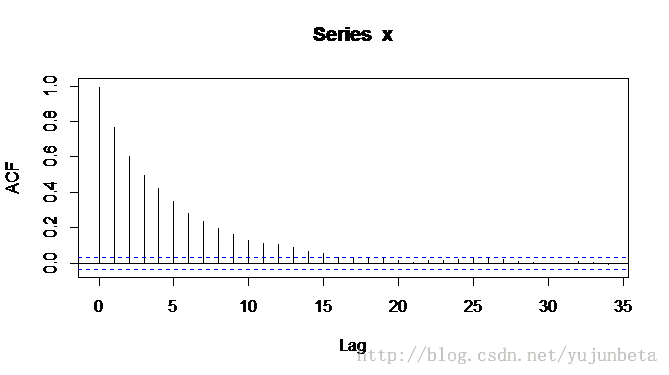
我们再来看看它们的自相关图:
我们开始做采样,从1000开始,每隔30步取一个数,构成新的数列z。我们对z与x分别作ks检验,有:
> z<-x[seq(1000,N,by=30)]
> ks.test(z,"pbeta",2,7)
One-sampleKolmogorov-Smirnov test
data: z
D = 0.1123, p-value = 0.3671
alternative hypothesis: two-sided
> ks.test(x[1000:N],"pbeta",2,7)
One-sampleKolmogorov-Smirnov test
data: x[1000:N]
D = 0.0894, p-value = 2.487e-14
alternative hypothesis: two-sided
可以看出,这样的采样是有必要的。
二、Metropolis-Hastings 算法
前面利用随机游走来产生随机数看上去已经很不错了,但是我们还是有一些遗憾:移动必须是对称的吗?当然没这个必要,Hastings在20世纪70年代时对前面提到的Metropolis算法做出了改进,得到了教科书里的Metropolis-Hastings 算法。
从理论上讲,提议函数q(x|xt)的选取是任意的,但在实际计算中,提议函数的选取对于算法的效率的影响是相当大的.一般认为提议函数的形式与目标分布越接近,则模拟的效果越好。如果M-H算法中的提议函数q(x|xt)不仅满足对称性,而且只与x-y有关,那么算法就演变为通常意义下的随机游动采样法。最常见的一种随机游动采样法以正态分布,即q(x,y)=φ(x-y)为提议函数。
我们以一个例子来说明Metropolis-Hastings算法的具体操作。
例:假设目标分布函数为N(3,5),提议函数采用随机游动,即新状态y~N(Xn,R),其中Xn为当前状态,R为标准差,取为2。
M-H算法的步骤如下:
- 1)取初值X1=100.
- 2)从提议函数N(Xn,R)中产生一个新状态y.
- 3)计算接受概率
- 4)以概率A(x,y)置Xn+1=y;以概率1-A(x,y)置Xn+1=x.
我们利用R语言实现如下:
N <-10000 #抽样个数
x <- c()
x0 <-100 # 初始值
x[1] <- x0
k <- 0 #k表示拒绝转移的次数
u <- runif(N) #抽取均匀分布随机数
for (i in 2:N) {
y <- rnorm(1, x[i - 1],2)
if (u[i] <(dnorm(y,3,5)/dnorm(x[i - 1],3,5)))
x[i] <- y else {
x[i] <- x[i - 1]
k <- k + 1
}
}
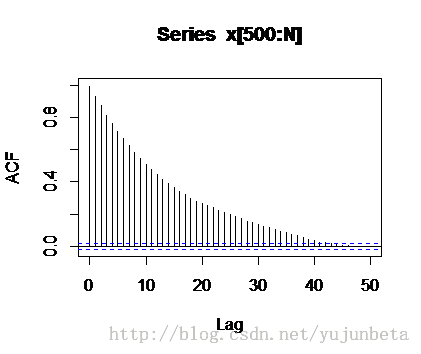
我们构造了一条长度为10000的Markov链,为了消除初值对采样的影响,从第500个样本开始取样分析.从直方图上看采样结果令人满意,估计的密度函数与目标分布函数十分接近。
运行以下代码:
> hist(x[500:N],freq=F)
> curve(dnorm(x,3,5),add=TRUE)
我们为了获得近似独立的样本,我们采取间隔采样法,观察acf图,有:
间隔45个值进行一次采样,ks检验的结果为:
One-sampleKolmogorov-Smirnov test
data: x
D = 0.0569, p-value = 0.4989
alternative hypothesis: two-sided
我们在结束这一小节之前,我们先考虑一个问题:提案分布应该怎么选?常见的提案分布大致有独立链与随机游走链。我们来看看独立链的情形,在独立链中,每一个候选值与前面的候选值相互独立,这种情况下,如果q(x)>0,只要p(x)>0,马氏链就是非周期不可约的。这个办法在Bayes推断中十分有用。
三、Bayes推断中的MCMC方法
Bayes学派与频率学派的一个不同就是bayes学派认为在参数统计中,参数是符合一个分布的,而不是一个确定的值。我们将MH中的提议函数看做是先验分布,那么将MH算法运用到Bayes推断中是十分自然的事情。
考虑似然方程L(theta|y),其中theta为参数,y为观测数据,参数theta的先验分布为p(theta)。贝叶斯推断基于后验分布p(theta|y)=cp(theta)L(theta|y),其中c为未知常数。我们很难通过计算得到后验分布,并以此做出推断。然而我们可以从马氏链中获得一个样本,使得样本马氏链的平稳分布是目标后验分布。于是,在Bayes统计中,使用MCMC方法可以很容易得到我们想要的样本。
我们这里最简单的办法就是将先验分布视为提案分布,那么metropolis比率可以化简为似然比。由定义,先验分布的支撑集覆盖后验分布的支撑集,因此独立链的平稳分布是我们想要的后验分布。
我们举一个可靠性推断的例子来说明MCMC方法在bayes推断中的应用。这个例子来自Dagpunar的Simulation and Monte Carlo with application in finance and MCMC一书。
问题描述如下:
数据:Failuretimes for 43 components
293, 1902, 1272,2987, 469, 3185, 1711, 8277, 356, 822, 2303, 317, 1066, 1181, 923, 7756, 2656,879, 1232, 697, 3368, 486, 6767, 484, 438, 1860, 113, 6062, 590, 1633, 2425,367, 712, 953, 1989, 768, 600, 3041, 1814, 141, 10511, 7796, 1462
R代码如下:
simulation<-function(iter,a0,b0,data,y){
a1<-a0 #威布尔分布的参数alpha的初始值
b1<-b0 #威布尔分布参数beta的初始值
n<-length(data)
q<-length(y) #这里y表示寿命界限。如y[1]=1000,表示1000小时后零件仍可以继续工作的概率,这个概率储存在C对应的列中。
C<-matrix(rep(0,iter*(q+2)),iter,q+2) #储存零件存活概率与alpha、beta的估计值
xp<-1
sp<-0
for(i in 1:n){
xp<-xp*data[i]
sp<-sp+data[i]^a1
}
xp<-log(xp)
l1<-n*log(a1/b1^a1)+(a1-1)*xp-sp/b1^a1 #对数似然函数
for(i in 1:iter){ #这个是似然函数的先验分布,也就是独立链里的提议分布。
r<-runif(4)
ap<-1+0.5*(r[1]+r[2])
bp<-1000*(2+r[3])/gamma(1/ap+1)
sp<-0
for(j in 1:n)
sp<-sp+data[j]^ap
l2<-n*log(ap/bp^ap)+(ap-1)*xp-sp/bp^ap#更新对数似然函数
if(log(r[4])<l2-l1){ #对metropolis比率取对数,更新参数
a1<-ap
b1<-bp
l1<-l2
}
C[i,]<-c(exp(-(y/b1)^a1),a1,b1)
}
return(C)
}
data<-c(293, 1902, 1272, 2987, 469, 3185, 1711, 8277,356, 822, 2303,
317, 1066, 1181,923, 7756, 2656, 879, 1232, 697, 3368, 486, 6767,
484, 438, 1860, 113, 6062, 590, 1633, 2425, 367, 712,953, 1989, 768,
600, 3041, 1814,141, 10511, 7796, 1462)
a0<-1.5
b0<-2500/gamma(1/a0+1)
iter<-5000
y<-c(1000,2000,3000)
result<-simulation(iter,a0,b0,data,y)
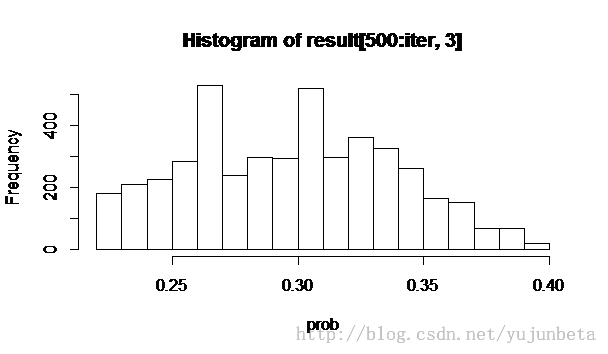
那么我们对零件使用超过3000小时的一个合理估计就是C[,3]的均值,0.2976153。从下面样本路径图与直方图可以看到,样本混合良好.
同样的,我们可以用alpha,beta估计的均值来估计alpha,beta,得到alpha= 1.14594,beta= 2543.654。
四、Gibbs抽样
Gibbs算法,是Metropolis-Hasting算法的一个特例,就是用条件分布的抽样来替代全概率分布的抽样。例如,X={x1,x2,...xn}满足分布p(X),如何对p(X)进行抽样呢?如果我们知道它的条件分布p(x1|X_{-1}),...,p(xi|X_{-i}),....,其中X_{-i}表示除了xi之外X的所有变量。如果这些条件分布都是很容易抽样的,那么我们就可以通过对条件分布的抽样来对全概率分布p(X)进行抽样。

当X的一个或者多个元素的一元边际密度没有显示表达时,不妨将Gibbs迭代中的那一步替换为Metropolis-Hastings迭代,这样会使问题简化很多。
我们这里仅以一个最简单的二元正态的例子来说明如何使用Gibbs抽样,R代码如下:
n <- 5000 #抽样个数(链的长度)
burn.in <- 2500 #前2000个抽样按burn-in处理
X <- matrix(0, n, 2)
mu1 <- 1 #对参数赋值
mu2 <- -1
sigma1 <- 1
sigma2 <- 2
rho <- 0.5
s1.c <- sqrt(1 - rho^2) * sigma1
s2.c <- sqrt(1 - rho^2) * sigma2
X[1, ] <- c(mu1, mu2) #初始化
for (i in 2:n) {
x2 <- X[i - 1, 2]
m1.c <- mu1 + rho * (x2 - mu2) * sigma1/sigma2
X[i, 1] <- rnorm(1, m1.c, s1.c)
x1 <- X[i, 1]
m2.c <- mu2 + rho * (x1 - mu1) * sigma2/sigma1
X[i, 2] <- rnorm(1, m2.c, s2.c)
}
b <- burn.in + 1
x.mcmc <- X[b:n, ]
这里需要指出的是如果只是需要生成多元正态分布,我们完全不需要这么麻烦的手段,直接使用一元正态在线性变换下生成多元正态的办法即可。这时你只需要对协方差阵做Cholesky分解即可。
Further reading
rickjin : LDA-math-MCMC和 Gibbs Sampling
本作品采用 知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。