Trie的java实现
关注Trie 这种结构已经很久,Trie有一个很有趣的用途,那就是自动提示。而且,前不久在一次面试里,也需要用Trie来解答。所以,在此对这个数据结构进行总结。
Trie,又称单词查找树或键树,是一种树形结构。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
它有3个基本性质:
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
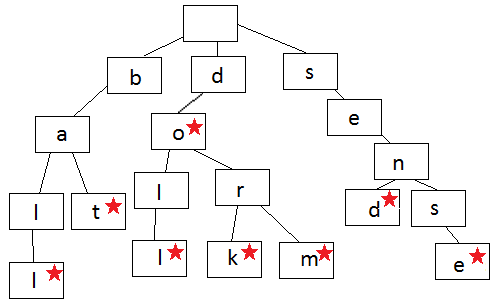
下面这个图就是Trie的表示,每一条边表示一个字符,如果结束,就用星号表示。在这个Trie结构里,我们有下面字符串,比如do, dork, dorm等,但是Trie里没有ba, 也没有sen,因为在a, 和n结尾,没有结束符号(星号)。
有了这样一种数据结构,我们可以用它来保存一个字典,要查询改字典里是否有相应的词,是否非常的方便呢?我们也可以做智能提示,我们把用户已经搜索的词存在Trie里,每当用户输入一个词的时候,我们可以自动提示,比如当用户输入 ba, 我们会自动提示 bat 和 baii.
现在来讨论Trie的实现。
首先,我们定义一个Abstract Trie,Trie 里存放的是一个Node。这个类里有两个操作,一个是插入,另一个是查询。具体实现放在后面。
Node 类的实现
class Node {
char content; // the character in the node
boolean isEnd; // whether the end of the words
int count; // the number of words sharing this character
LinkedList<Node> childList; // the child list
public Node(char c){
childList = new LinkedList<Node>();
isEnd = false;
content = c;
count = 0;
}
public Node subNode(char c){
if(childList != null){
for(Node eachChild : childList){
if(eachChild.content == c){
return eachChild;
}
}
}
return null;
}
}
现在我们来看这个Trie类的具体实现。
public class Trie{
private Node root;
public Trie(){
root = new Node(' ');
}
public void insert(String word){
if(search(word) == true) return;
Node current = root;
for(int i = 0; i < word.length(); i++){
Node child = current.subNode(word.charAt(i));
if(child != null){
current = child;
} else {
current.childList.add(new Node(word.charAt(i)));
current = current.subNode(word.charAt(i));
}
current.count++;
}
// Set isEnd to indicate end of the word
current.isEnd = true;
}
public boolean search(String word){
Node current = root;
for(int i = 0; i < word.length(); i++){
if(current.subNode(word.charAt(i)) == null)
return false;
else
current = current.subNode(word.charAt(i));
}
/*
* This means that a string exists, but make sure its
* a word by checking its 'isEnd' flag
*/
if (current.isEnd == true) return true;
else return false;
}
public void deleteWord(String word){
if(search(word) == false) return;
Node current = root;
for(char c : word.toCharArray()) {
Node child = current.subNode(c);
if(child.count == 1) {
current.childList.remove(child);
return;
} else {
child.count--;
current = child;
}
}
current.isEnd = false;
}
public static void main(String[] args) {
Trie trie = new Trie();
trie.insert("ball");
trie.insert("balls");
trie.insert("sense");
// testing deletion
System.out.println(trie.search("balls"));
System.out.println(trie.search("ba"));
trie.deleteWord("balls");
System.out.println(trie.search("balls"));
System.out.println(trie.search("ball"));
}
}
时间复杂度分析:
对于insert, 如果被插入的String长度是 k, 每对一个字符进行查询,我们最多在child linkedlist里面查询26次(最多26个字母),所以,复杂度为O(26*k) = O(k). 对于 search, 复杂度是一样的。