poj 3565（计算几何，线段相交）

Ants

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 5907		Accepted: 1828		Special Judge

Description

Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.

Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.

Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.

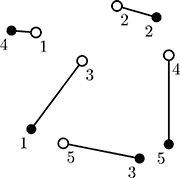
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.

Input

The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (− 10 000  ≤ x, y ≤  10 000 ) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.

Output

Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.

Sample Input

5
-42 58
44 86
7 28
99 34
-13 -59
-47 -44
86 74
68 -75
-68 60
99 -60

Sample Output

4
2
1
5
3


解题思路：这题一开始的想法就是用匈牙利算法+线段相交判定，结果思路是错的。因为匈牙利算法目的是找增广路，而题目是要保证线段不相交，这两个要求无法取交集。可以任意假定一种组合，然后两两判断，如果相交，则交换，直到全部不相交为止。
参考博客：
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

const int maxn = 105;
const double eps = 1e-8;
struct Point
{
	double x,y;
}ant[maxn],tree[maxn];
int n,match[maxn];

double Cross(Point a,Point b,Point c)    
{    
    return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);    
}    

bool SegmentAcross(Point s1a,Point s1b,Point s2a,Point s2b){  
    if(max(s1a.x,s1b.x) >= min(s2a.x,s2b.x) && max(s2a.x,s2b.x) >= min(s1a.x,s1b.x)  
    &&max(s1a.y,s1b.y)>=min(s2a.y,s2b.y)&&max(s2a.y,s2b.y)>=min(s1a.y,s1b.y))  
        if(Cross(s1a,s1b,s2a)*Cross(s1a,s1b,s2b)<-eps)  
            if(Cross(s2a,s2b,s1a)*Cross(s2a,s2b,s1b)<-eps)  
                return true;  
    return false;  
}  

int main()
{
	while(scanf("%d",&n)!=EOF)
	{
		for(int i = 1; i <= n; i++)
			scanf("%lf%lf",&ant[i].x,&ant[i].y);
		for(int i = 1; i <= n; i++)
			scanf("%lf%lf",&tree[i].x,&tree[i].y);
		for(int i = 1; i <= n; i++)
			match[i] = i;   //先确定出一种方案，然后再交换。
		while(true)
		{
			bool ok = true;
			for(int i = 1; i <= n; i++)
				for(int j = 1; j <= n; j++)
				{
					if(SegmentAcross(ant[i],tree[match[i]],ant[j],tree[match[j]]))
					{  
                       swap(match[i],match[j]);  
                       ok = false;  
					}  
				}
			if(ok) break;
		}
		for(int i = 1; i <= n; i++)
			printf("%d\n",match[i]);
	}
	return 0;
}