Java实现——二叉查找树
- TreeNode.java
package com.thomas.datastructure.BST;
public class TreeNode
{
private int data;
private TreeNode leftChild;
private TreeNode rightChild;
private TreeNode parent;
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public TreeNode getParent() {
return parent;
}
public void setParent(TreeNode parent) {
this.parent = parent;
}
public TreeNode getLeftChild() {
return leftChild;
}
public void setLeftChild(TreeNode leftChild) {
this.leftChild = leftChild;
}
public TreeNode getRightChild() {
return rightChild;
}
public void setRightChild(TreeNode rightChild) {
this.rightChild = rightChild;
}
public TreeNode(){}
public TreeNode(int data, TreeNode leftChild, TreeNode rightChild) {
this.data = data;
this.leftChild = leftChild;
this.rightChild = rightChild;
}
}
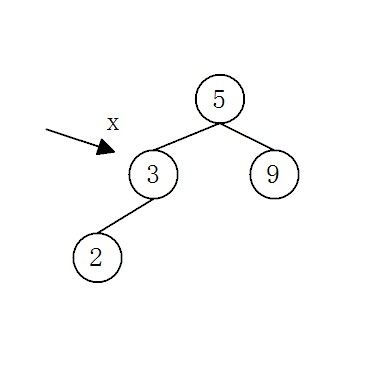
PS:parent域的存在是为了辅助二叉查找树的删除操作。因为Java中没有指针,所有对于对象的操作,都是通过栈上的引用来进行的,无法直接对堆中的内存进行操作。举例如下,删除一个结点
如果是C,可以类似下面这样写:
TreeNode temp = *x;
*x = (*x)->leftChild;
free(temp);Java的话,根本就不可能啊。要重设5的左孩子为2,那必须调用5这个TreeNode对象的setLeftChild()方法。所以要删除3这个结点,必须知晓5的存在,所以要有parent域。当然,也可以每次删除时,都遍历二叉查找树,以得到欲删除节点的父结点。但时间花费较大,而且,如果是红黑树,遍历得到父结点的情况就更多了,左旋、右旋都要遍历,其时间花费相当大。因此,parent域有存在的必要性,以空间代价换时间代价。不过,这个域的存在也让后面的删除操作变得繁琐一些。如果是红黑树的话,涉及到左旋、右旋,就更繁琐了。
- BinaySortTree.java
package com.thomas.datastructure.BST;
import java.util.ArrayList;
import java.util.List;
public class BinarySortTree {
//中序遍历缓存
private List<Integer> midOrderVisitList = new ArrayList<Integer>();
//类似于链表中的头指针
//为了方便删除结点,并无实际的业务功能
//它的左孩子才是真正的根结点
private TreeNode fakeRoot;
public BinarySortTree(TreeNode root)
{
this();
fakeRoot.setLeftChild(root);
root.setParent(fakeRoot);
}
public BinarySortTree()
{
fakeRoot = new TreeNode(-1, null, null);
fakeRoot.setParent(null);
}
public boolean isEmpty()
{
return fakeRoot.getLeftChild() == null;
}
/** * 递归查询某个数据是否在树中 * @param node 指定的子树 * @param data 要查找的数据 * @param parent 子树的父结点 * @return 结果结点。若有匹配数据项,则返回对应结点。若无匹配,则返回叶子结点 */
private TreeNode search(TreeNode node, int data, TreeNode parent)
{
//子树为空(空结点),即找不到匹配的结点
//此时parent有三种情况:
//1、叶结点 2、仅有左子树 3、仅有右子树
//返回parent是为了方便进行插入操作,因为插入一个结点要先search
if(null == node)
return parent;
int _data = node.getData();
if(_data == data)
return node;
//左子树或右子树递归查找
if(data < _data)
return search(node.getLeftChild(), data, node);
return search(node.getRightChild(), data, node);
}
/** * 非递归查询某个数据项是否在树中 * @param node 指定的子树 * @param data 要查找的数据 * @return 结果结点。若有匹配数据项,则返回对应结点。若无匹配,则返回叶子结点 */
private TreeNode search(TreeNode node, int data)
{
TreeNode parent = null;
while(node != null)
{
int _data = node.getData();
if(_data == data)
return node;
parent = node;
if(data < _data)
node = node.getLeftChild();
else
node = node.getRightChild();
}
return parent;
}
//对外提供的查询接口
//具体的实现可使用递归查询,也可不使用递归查询
public TreeNode search(int data)
{
if(!isEmpty())
// return search(root, data, null);
return search(fakeRoot.getLeftChild(), data);
return null;
}
private void midOrderVisit(TreeNode tree, List<Integer> dataList)
{
if(null == tree)
return;
midOrderVisit(tree.getLeftChild(), dataList);
dataList.add(tree.getData());
midOrderVisit(tree.getRightChild(), dataList);
}
public List<Integer> midOrderVisit()
{
//中序缓存列表中有数据,则无须再次遍历,直接返回该列表
if(midOrderVisitList.size() == 0)
midOrderVisit(fakeRoot.getLeftChild(), midOrderVisitList);
return midOrderVisitList;
}
public boolean insert(int data)
{
TreeNode resultTree = search(data);
//空树
if(resultTree == null)
{
TreeNode root = new TreeNode(data, null, null);
fakeRoot.setLeftChild(root);
root.setParent(fakeRoot);
return true;
}
//原树中已经有该数据项,不必插入
int _data = resultTree.getData();
if(data == _data) return false;
//非空树
TreeNode newTree = new TreeNode(data, null, null);
if(data < _data)
resultTree.setLeftChild(newTree);
else resultTree.setRightChild(newTree);
newTree.setParent(resultTree);
//树结构变化,中序缓存清空
midOrderVisitList.clear();
return true;
}
public boolean delete(int data)
{
//空树
if(isEmpty()) return false;
TreeNode target = search(data);
//树中不存在该数据,无法删除
int targetData = target.getData();
if(targetData != data) return false;
final TreeNode parent = target.getParent();
final TreeNode left = target.getLeftChild();
final TreeNode right = target.getRightChild();
//叶结点
if(left == null && right == null)
{
if(target == parent.getLeftChild())
parent.setLeftChild(null);
else parent.setRightChild(null);
target = null;
}
//仅有左子树
else if(target.getRightChild() == null)
{
if(target == parent.getLeftChild())
parent.setLeftChild(left);
else parent.setRightChild(left);
left.setParent(parent);
target = null;
}
//仅有右子树
else if(target.getLeftChild() == null)
{
if(target == parent.getLeftChild())
parent.setLeftChild(right);
else parent.setRightChild(right);
right.setParent(parent);
target = null;
}
//左右子树均有
else
{
//找到欲删除结点的左子树的右分支尽头的叶结点
//以之替换欲删除的结点的位置
TreeNode temp = target.getLeftChild();
while(temp.getRightChild() != null)
temp = temp.getRightChild();
target.setData(temp.getData());
TreeNode tempLeftChild = temp.getLeftChild();
TreeNode tempParent = temp.getParent();
//temp的父结点仍等于target结点
//说明循环并没有执行,即target的左子树并没有右分支
if(tempParent == target)
tempParent.setLeftChild(tempLeftChild);
else
tempParent.setRightChild(tempLeftChild);
if(null != tempLeftChild)
tempLeftChild.setParent(tempParent);
temp = null;
}
//树结构变化,中序缓存清空
midOrderVisitList.clear();
return true;
}
}
PS:fakeRoot的主要作用是把根结点与其他结点的删除操作给等效起来了,不用特意判断欲删除结点是不是根结点。要不然因为根结点的parent为null,会抛NullPointerException。其作用类似于链表中的头结点。当然,这只是本人针对Java而使用的一个trick,如果有更好的解决思路,请联系告知,先行谢过。
- Client.java
package com.thomas.datastructure.BST;
import java.util.Arrays;
import java.util.List;
import java.util.Random;
import java.util.Scanner;
public class Client
{
public static void main(String[] args)
{
System.out.println("specify the length and the max:");
Scanner scanner = new Scanner(System.in);
int len = scanner.nextInt();
int max = scanner.nextInt();
int[] array = new int[len];
Random random = new Random();
for(int i = 0; i < len; ++i)
array[i] = random.nextInt(max);
System.out.println(Arrays.toString(array));
TreeNode root = new TreeNode(array[0], null, null);
BinarySortTree tree = new BinarySortTree(root);
for(int i = 1; i < len; ++i)
tree.insert(array[i]);
List<Integer> midOrderVisit = tree.midOrderVisit();
System.out.println(Arrays.toString(midOrderVisit.toArray(new Integer[]{})));
int deleteKey = 0;
do{
System.out.println("the element you wanna delete: ");
deleteKey = scanner.nextInt();
if(deleteKey < 0)
break;
if(!tree.delete(deleteKey))
System.out.println("not in the tree");
else
{
midOrderVisit = tree.midOrderVisit();
System.out.println( Arrays.toString(midOrderVisit.toArray(new Integer[]{})));
}
}while(midOrderVisit.size() > 0);
scanner.close();
System.out.println("Exit!!!");
}
}
PS:简单地测试了一下而已,可能有所疏忽。若有bug请告知,共同探讨。