微软面试100题系列-第1题
写文的目的是锻炼自己,欢迎各位大牛提出建议,批评指正~
第一题:把二分查找树转变成排序的双向链表
输入一棵二分查找树,将该二分查找树转换成一个排序的双向链表。要求不能创建任何新的结点,只调整指针的指向。如:
10
/ \
6 14
/ \ / \
4 8 12 16
转换成双向链表4=6=8=10=12=14=16 。
我们定义的二分查找树结点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
我的解题思路如下:
本题中不能建立新的结点,只能改变指针的指向。先观察根结点,根据二叉查找树的特点,可以发现根结点的左指针应该指向左子树双向链表的尾部,而根结点的右指针
应该指向右子树双向链表的头部。因此该问题可以递归为求解左、右孩子的双向链表。求解完左、右孩子的双向链表后,再接上根结点,即可完成对双向链表的求解。
根据上述思路,先来看一下代码结构,之后会有例子讲解。
编写如下的递归函数:
void ConvertRecursive(BSTNode* &subHead, BSTNode* &subTail, BSTNode* subRoot)
然后在函数中求解左、右孩子的双向链表:
BSTNode *leftTail = NULL, *rightHead = NULL;
ConvertRecursive(subHead,leftTail,subRoot->pLeft); //求解左子的链表
ConvertRecursive(rightHead,subTail,subRoot->pRight); //求解右子的链表
。。。。。。 //将左子链表、根、右子链表连接起来
这个递归初看可能有点不清晰,我们可以先看一下求解左子链表的语句:
ConvertRecursive(subHead,leftTail,subRoot->pLeft);
这个subHead可看成是当前链表的头,在递归结束后,最上一层的subHead将是整个双向链表的头。而leftTail是我们想要的左孩子双向链表的尾部。
ConvertRecursive(rightHead,subTail,subRoot->pRight);
rightHead是我们想要的右孩子双向链表的头部,而subTail可看成是当前链表的尾,在递归结束后,最上一层的subTail将是整个双向链表的尾。
现在看一下左子链表、根与右子链表连接的操作:如果左子没有双向链表,那么根结点就成为当前链表的头;如果有,根结点就连接上左子链表的尾部。
同理,如果右子没有链表,那么根结点就成为当前链表的尾;如果有,则根结点与右子链表的头部相连接。
//连接左子链表与根
if (leftTail == NULL) //左子没有双向链表
{
subHead = subRoot;
}
else
{
leftTail->pRight = subRoot;
subRoot->pLeft = leftTail;
}//连接右子链表与根
if (rightHead == NULL) //右子没有双向链表
{
subTail = subRoot;
}
else
{
subRoot->pRight = rightHead;
rightHead->pLeft = subRoot;
}
以子树 6 为例,
/ \
4 8
递归到4时,因为4是叶子结点,其左、右子树链表为空,则有subHead -> 4, subTail -> 4。同理8也是这种情况。
返回到6的调用,因为6调用4的递归中,形参subTail实际上是实参leftTail的引用,因此6的左子链表leftTail->4不为空,按照之前的思路,我们可以将结点6与左子链表连
接起来,就有了链表4=6;同理,在6调用8的递归中,形参subHead实际上是实参rightHead的引用,因此6的右子链表rightHead->8也不为空,将6与右子链表连接起来,我们
有了双向链表4=6=8,而此时当前链表的subHead->4,subTail->8。
由此,可以看出整个递归过程中,leftTail和rightHead起到了连接整个链表中间结点的作用,而subHead和subTail则保存了目前递归层次中的最小和最大值。
完整的代码如下,因为自己有一个BST树结点的模板类,所以直接拿来用了,BSTNode<int>和题目中的BSTreeNode的结构是一样的。
//written by zero
#include "BST.h"
#include <iostream>
using namespace std;
void ConvertRecursive(BSTNode<int>* &subHead, BSTNode<int>* &subTail, BSTNode<int>* subRoot)
{
BSTNode<int> *leftTail = NULL, *rightHead = NULL;
if (subRoot == NULL)
{
subHead = NULL;
subTail = NULL;
return;
}
ConvertRecursive(subHead,leftTail,subRoot->pLeft); //求解左子的链表
ConvertRecursive(rightHead,subTail,subRoot->pRight); //求解右子的链表
//将左子链表,根,右子链表接在一起
//连接左子链表与根
if (leftTail == NULL) //左子没有双向链表
{
subHead = subRoot;
}
else
{
leftTail->pRight = subRoot;
subRoot->pLeft = leftTail;
}
//连接右子链表与根
if (rightHead == NULL) //右子没有双向链表
{
subTail = subRoot;
}
else
{
subRoot->pRight = rightHead;
rightHead->pLeft = subRoot;
}
}
int main()
{
//建立二叉查找树
BSTree<int> tree;
tree.Insert(10);
tree.Insert(6);
tree.Insert(14);
tree.Insert(4);
tree.Insert(8);
tree.Insert(12);
tree.Insert(16);
/*tree.TravelRecursive(&BSTree<int>::PosOderRecursive,&BSTree<int>::process);
cout << endl;
tree.TravelRecursive(&BSTree<int>::PosOderNonRecursive,&BSTree<int>::process);
cout << endl;*/
//转换成双向链表
BSTNode<int> *head = NULL, *tail = NULL, *pNode;
ConvertRecursive(head,tail,tree.root);
//验证正向遍历双向链表
cout << "正向遍历链表:";
pNode = head;
while(pNode)
{
cout << pNode->value << " ";
pNode = pNode->pRight;
}
cout << endl;
//验证逆向遍历双向链表
cout << "逆向遍历链表:";
pNode = tail;
while(pNode)
{
cout << pNode->value << " ";
pNode = pNode->pLeft;
}
cout << endl;
}
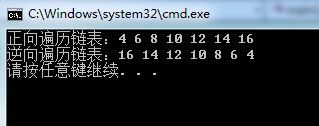
运行结果如下: