- 纳米尺度仿真软件:Quantum Espresso_(18).纳米结构的几何优化
kkchenjj
分子动力学2模拟仿真分子动力学仿真模拟
纳米结构的几何优化在纳米尺度仿真软件中,几何优化是计算材料性质的重要步骤之一。几何优化的目标是找到系统的最低能量构型,这通常涉及到调整原子的位置以使系统的总能量最小化。在本节中,我们将详细介绍如何在QuantumEspresso中进行几何优化,并提供具体的代码示例和数据样例。几何优化的基本概念几何优化是通过迭代调整原子的位置来使系统的总能量最小化的过程。在每一步迭代中,软件会计算系统的梯度(即能量
- 深入GPU渲染流水管线:从顶点到像素的微观世界
晴空了无痕
图形学GPU渲染管线
现代图形硬件的架构解密与优化实践一、渲染流水线全景解析1.经典渲染管线阶段划分应用阶段几何阶段光栅化阶段像素处理阶段输出合并阶段2.现代GPU架构演进SIMT架构特性:NVIDIASM(StreamingMultiprocessor)vsAMDCU(ComputeUnit)硬件管线并行度:顶点着色器:32线程/Warp像素着色器:8x8像素/Quad延迟渲染革命:Tile-BasedDeferre
- DeepBranchTracer:一种使用多特征学习进行曲线结构重建的通用方法
数据集
2024-02-02,由刘超、赵婷、郑能干一起提出了一种名为DeepBranchTracer的新型方法,是一种高效、通用的曲线结构重建方法,适用于多种2D和3D图像数据集。通过结合图像特征和几何特征,显著提高了重建的准确性和连续性。一、研究背景曲线结构(curvilinearstructures)是图像中常见的几何元素,广泛应用于医学图像中的神经分支和血管,以及遥感图像中的道路等。从图像中重建这些
- Cesium在三维模型中的应用
IT邦少
前端贴图
Cesium在三维模型中的应用Cesium简介Cesium介绍Cesium是一个跨平台,跨浏览器的展示三维地球和地图的javascript库Cesium使用WebGL来进行硬件加速图形,使用时不需要任何插件支持,但是浏览器必须支持WebGLCesium是基于Apache2.0许可的开源程序,它可以免费的用于商业和非商业用途Cesium特点支持2D,2.5D,3D形式的地图展示可以绘制各种几何图形,
- 算法刷题汇总 python版本
lanlinbuaa
python算法leetcode
OJ在线编程常见输入输出练习牛客网练习链接:https://ac.nowcoder.com/acm/contest/5657#question1.读取行数未知方法一:使用forlineinsys.stdinimportsysforlineinsys.stdin:a=line.split()#split()默认为所有的空字符,包括空格、换行(\n)、制表符(\t)等print(int(a[0])+i
- 计算机视觉(Computer Vision, CV)的入门到实践的详细学习路线
云梦优选
计算机数据库大数据计算机视觉学习人工智能
一、基础准备1.数学基础线性代数深入矩阵运算,理解矩阵乘法、转置、逆等基本概念。掌握特征值与特征向量的几何意义,理解其在图像压缩、特征提取中的应用。学习奇异值分解(SVD)及其在降维和数据压缩中的具体应用。概率与统计熟悉贝叶斯定理及其在分类任务中的应用,如朴素贝叶斯分类器。理解常见概率分布(如正态分布、二项分布)及其性质。学习统计推断方法,如假设检验、置信区间估计,以评估模型性能。微积分掌握梯度、
- 3月份学习任务、工作计划
Kamui_0us
学习
3月18日报名六级3月22日之前收集团日材料3月22日收集五四述职材料3月29日计算解二级学英语:为了六级为了绩点为了大英赛为了雅思接续规划留学计划恶补数学,拉下的慢慢补回来今日学习任务:学习本周的解析几何课程,背六级单词,还有时间可以看看github有关知识
- Mac下安装Zed以及Zed对MCP(模型上下文协议)的支持
skywalk8163
人工智能macos前端服务器
Zed是当前新流行的一种编辑器,支持MCP(模型上下文协议)Mac下安装Zed比较简单,直接有安装包,在这里:brewinstall--caskzedMacMonterey下是可以安装上的,亲测有效。配置使用Ctrl+Shift+P调出AI,然后设置使用的模型可以使用deepseek,但是没有找到使用自建服务器的设置方法,有些遗憾。附加学习关于Zed里面的MCP部分,手册:ModelContext
- JavaScript性能优化指南:聚焦DOM操作优化
桃木山人
技术杂谈javascript性能优化开发语言
引言:性能优化的关键路径在Web应用开发中,JavaScript性能直接影响用户体验。虽然存在多种优化手段,但DOM操作优化往往能带来最显著的性能提升。本文将以DOM操作为核心展开深入分析,并简要概述其他优化方向。核心优化:DOM操作性能提升1.问题根源分析浏览器渲染引擎与JavaScript引擎独立运作,频繁的DOM操作会导致:重排(Reflow):计算元素几何属性重绘(Repaint):更新元
- PCL 点云OBB包围盒(二)
大鱼BIGFISH
点云进阶C++PCL点云OBB包围盒
文章目录一、简介二、实现步骤二、实现代码三、实现效果参考资料一、简介包围盒是一种求解离散点集最优包围空间的算法,基本思想是用体积稍大且特性简单的几何体(称为包围盒)来近似地代替复杂的几何对象。(来源于百度)常用的求解包围盒的算法主要有AABB和OOB算法,但AABB算法容易受到物体朝向的影响,产生较大的空隙,因此本文将以OOB算法思想实现最小包围盒的求取。包围盒的应用有很多,如机械上的碰撞测试、物
- 基于PySide6与PyCatia的CATIA几何体智能重命名工具开发实践
Python×CATIA工业智造
python开发语言CATIA二次开发
一、工具概述本工具基于CATIAV5/V6的二次开发接口,结合PySide6图形界面框架与PyCatia自动化库,实现了三大核心功能模块:几何体前缀批量添加、后缀动态追加、智能文本替换。该工具显著提升了工程师在大型零件体设计中的几何体命名管理效率,解决了传统手动操作易出错、耗时长的问题。二、技术架构解析1.分层架构设计classStats(QMainWindow):def__init__(self
- 《计量地理学》实习指南
zmg18213828575
一、EXCEL中常用的函数(部分)操作方法:打开EXCEL→输入原始数据→选择fx粘贴函数→函数分类中选择统计→从函数名中选择我们所需要的函数→确定→在数值中输入或选入计算数据范围(如A1:A10)则结果就会出来。具体的函数及其含义:AVERAGE计算参数平均值CORREL求相关系数DEVSQ求离差平方和FTESTF检验的结果GEOMEAN正数数组的几何平均数INTERCEPT一元回归线的载距(Y
- 三维空间的秘密:3D数学背后的几何之美!
程序边界
3d
文章目录一、3D数学的核心概念1.1向量(Vector)1.2矩阵(Matrix)1.3坐标系(CoordinateSystem)二、3D数学的应用场景2.1三维建模与动画2.2光照与阴影2.3物理模拟三、如何学习与实践3D数学3.1学习资源推荐3.2实践建议四、未来展望《3D数学基础:图形和游戏开发(第2版)》内容简介目录解密向量、矩阵与坐标系的魔法,感受3D数学在科技与艺术中的无限魅力!在计算
- 在雷池社区版 WAF 通过文件更新 SSL 证书的方法
运维服务器ubuntu
有些用户在使用雷池WAF的证书管理功能时,觉得手动申请的证书需要去界面上传一次略显繁琐,想通过一个固定的目录存储证书文件,覆盖后让雷池自动检测并更新,这样可以通过一些自动化工具来完成整个流程。相关的ISSUE有:证书增加使用路径导入方式手动更新证书文件并重启容器后,【证书管理】界面的有效期时间没有同步关于结合acme.sh自动部署证书的建议因此为了解决或者优化上面的问题,雷池社区版在7.2.0版本
- AI大模型:教育行业的革新引擎
AI360labs_atyun
人工智能AIdeepseek
凌晨两点,高中生小林对着数学卷子抓耳挠腮。她轻触桌面的全息投影,AI助手“DeepSeek-R1”立刻扫描题目:“这道几何题需要先构建辅助线,还记得昨天练习的相似三角形判定法吗?”随即调出3D动态演示,讲解着自己的解题思路。指导小林轻松愉快的完成了复杂的作业。我们再试想一下:深夜两点,某重点中学教师仍在伏案批改作业这在以前可能是教师职业的常态,但是随着AI的普及。借助DeepSeek大模型,教师
- 回流(Reflow)与重绘(Repaint):原理、性能影响与优化策略
冬冬小圆帽
前端javascripthtml
回流(Reflow)和重绘(Repaint)是浏览器渲染页面时的两个关键过程,它们对页面性能有重要影响。理解它们的机制以及如何优化,可以帮助我们编写更高效的代码。下面我们将结合代码深度分析回流和重绘。1.回流和重绘的基本概念1.1回流(Reflow)回流是指浏览器计算页面布局的过程。当页面中的元素发生几何属性(如宽度、高度、位置等)变化时,浏览器需要重新计算元素的几何信息,并重新构建渲染树(Ren
- 计算机视觉算法实战——图像配准(主页有源码)
喵了个AI
计算机视觉实战项目计算机视觉
✨个人主页欢迎您的访问✨期待您的三连✨✨个人主页欢迎您的访问✨期待您的三连✨✨个人主页欢迎您的访问✨期待您的三连✨1.领域简介图像配准(ImageRegistration)是计算机视觉中的一个重要研究方向,旨在将两幅或多幅图像在空间上对齐。这些图像可能来自不同的传感器、不同的时间或不同的视角。图像配准在医学影像、遥感、自动驾驶、机器人导航等领域有着广泛的应用。其核心目标是通过几何变换(如平移、旋转
- 《Unity开发实战》——1.5节把Unity中创建的资源另存为Prefab
weixin_33859504
游戏
本节书摘来自华章社区《Unity开发实战》一书中的第1章,第1.5节把Unity中创建的资源另存为Prefab,作者(爱尔兰)MattSmith(巴西)ChicoQueiroz,更多章节内容可以访问云栖社区“华章社区”公众号查看1.5把Unity中创建的资源另存为Prefab在Unity中很容易就能创建基础几何对象,本节中,使用Unity的资源创建一个游戏对象(GameObject)然后将其在项目
- 在M4 Mac Mini集群上运行DeepSeek V3 671B
强化学习曾小健
Deepseek原理与使用macos
在M4MacMini集群上运行DeepSeekV3671B原创咖农小黄幻想发生器2024年12月30日10:50天津我们刚刚在苹果硅芯片上运行了最大的开源模型。直接来看在8台M4Pro64GBMacMini集群(总内存512GB)上运行DeepSeekv3(671B)的结果:模型首个Token时间(秒)每秒Token数DeepSeekV3671B(4位)2.915.37Llama3.1405B(4
- HDU多校2019 第三场 1007(HDU 6609) Find the answer(离散化+树状数组)
沙雕.
2019HDU多校
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6609解题思路:先把给出来的值离散化,对于值相同位置不同的数离散化后的值不相同。两个树状数组,一个维护区间内的和,一个维护区间内的个数。对于每个i二分答案,找到右界之后询问第二个树状数组得到剩余的个数x,那么去掉的就是(i-1)-x代码:(注意行末空格)#include#include#include#
- 重构:封装记录
Allenonlywork
重构
曾用名:以数据类取代记录(ReplaceRecordwithDataClass)//重构前organization={name:"AcmeGooseberries",country:"GB"};//重构后classOrganization{constructor(data){this.name=data.name;this._country=data.country;}getname(){retu
- Python自定义鼠标指针工具(支持像素级编辑)
木木黄木木
python计算机外设开发语言
Python自定义鼠标指针工具(支持像素级编辑)项目简介这是一个基于Python的鼠标指针自定义工具,可以让用户自由创建、编辑和设置Windows系统的鼠标指针。该工具提供了像素级编辑功能,支持多种绘图工具,并且可以直接将设计好的指针应用到系统中。主要功能像素级编辑器支持16x16到64x64多种尺寸铅笔、橡皮擦工具直线、矩形、圆形等几何图形工具填充/空心图形选择取色器功能热点设置可视化热点标记精
- seacmsv9注入
2022计科一班唐文
oracle数据库
一、当注入时,information_schema被禁用的解决方法information_schema数据库是MySQL和其他一些数据库系统中存储元数据的标准视图,包含表、列、权限等信息。攻击时可以直接查询这些信息来获取数据库结构,比如表名和列名。当information_schema被禁用时需要寻找其他途径来获取必要的信息。在information_schema数据库中储存了整个MySQL服务器
- 仿射变换矩阵应用
点云学习
c++pcl点云处理算法pcl点云处理3D视觉
目录1原理介绍2数学公式推导3计算流程4示例代码仿射变换是计算机视觉、图像处理和点云处理中常用的几何变换之一。它不仅包括旋转和平移,还包括缩放和剪切等线性变换。仿射变换保持了点、直线和平面的平行性。1原理介绍仿射变换在三维空间中通常由一个3×3的线性变换矩阵和一个3×1的平移向量组成。通过使用齐次坐标,我们可以将仿射变换表示为一个4×4矩阵:其中:A是一个3×3的线性变换矩阵(包含旋转、缩放、剪切
- 《几何原本》命题I.27
AllenAC
《几何原本》学习笔记
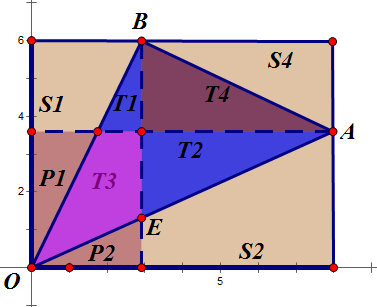
《几何原本》命题I.27内错角相等,两直线平行。设∠AEF=∠EFD,AB∦CD\angleAEF=\angleEFD,AB\nparallelCD∠AEF=∠EFD,AB∦CD,交CDCDCD于GGG则∠AEF\angleAEF∠AEF是△EGF\triangleEGF△EGF的外交角且=∠EFD=\angleEFD=∠EFD,矛盾则AB∥CDAB\parallelCDAB∥CD
- 递推和递归_一文学会递归递推
HR刀姐
递推和递归
递归算法和递推算法无论是在ACM竞赛还是项目工程上都有着极为广泛的应用,但想要完全掌握两者的思想并不容易,对于刚刚接触编程的人来说更是这样,我在初次接触递归递推时就吃了很多的苦头,除了当时对编程语言不太熟悉之外,最大的原因就是难以理解其中的思想,本文将二者结合代码分别讲解,力求以"理论+实践"的方式使读者明白两种算法。一箭双雕,一文双递。一.递归和递推的区别学习递归递推的一个容易遇到的问题就是混淆
- LWC-KD:图结构感知的推荐系统增量学习对比知识蒸馏
宇直不会放弃
GKD-Middlelayer人工智能pythonchatgptgpu算力深度学习机器学习神经网络
LWC-KD:图结构感知的推荐系统增量学习对比知识蒸馏《GraphStructureAwareContrastiveKnowledgeDistillationforIncrementalLearninginRecommenderSystems》2021作者是YueningWang、YingxueZhang和MarkCoates论文地址:https://dl.acm.org/doi/10.1145/
- 成功案例丨开发时间从1小时缩短到3分钟:如何利用历史数据训练AI模型,预测设计性能?
Altair澳汰尔
PhysicsAI仿真AI机器学习HyperWorks数据分析
案例简介PhysicsAI™助力HEROMOTOCORP实现设计效率提升99%印度领先的跨国摩托车和踏板车制造商HeroMotoCorpLtd.(以下简称Hero)致力于通过将人工智能(AI)和机器学习技术融入有限元分析(FEA)流程,以加速产品开发周期。在其首个AI驱动项目——摩托车把手设计优化中,Hero采用了PhysicsAI™几何深度学习解决方案,利用历史数据训练AI模型并预测设计性能。A
- 数学建模与优化算法在确定X和Y值时,如何处理实验数据的不确定性?
学术乙方
油纸绝缘算法经验分享
在数学建模与优化算法中处理实验数据的不确定性以确定油纸绝缘系统中的X和Y值,可以参考以下方法和步骤:建立数学模型油纸绝缘系统的几何结构可以用X-Y模型来描述,其中X表示挡板厚度与总厚度的比值,Y表示间隔器宽度与总宽度的比值。这些参数直接影响油纸绝缘的介电特性。通过实验数据(如介电谱曲线)和理论模型,可以建立数学方程来描述X和Y对介电特性的影响。引入不确定性建模实验数据通常存在测量误差、环境变化等因
- 服装消费“变天”,行业风向几何?
xss
服装消费环境之变:现象初窥不知你是否留意到,曾经热闹非凡的商场里,一些熟悉的服装品牌门店正在悄然减少。ZARA姐妹品牌Oysho从中国市场撤退,大量门店关闭,就连天猫旗舰店也于2024年11月17日关闭,这一事件引发了不少消费者的感慨。而这并非个例,太平鸟业绩连续三年下滑,2024年营业收入68.31亿元,同比下降12.34%;归母净利润2.57亿元,同比下降39.06%,大规模关店也在同步进行。
- 怎么样才能成为专业的程序员?
cocos2d-x小菜
编程PHP
如何要想成为一名专业的程序员?仅仅会写代码是不够的。从团队合作去解决问题到版本控制,你还得具备其他关键技能的工具包。当我们询问相关的专业开发人员,那些必备的关键技能都是什么的时候,下面是我们了解到的情况。
关于如何学习代码,各种声音很多,然后很多人就被误导为成为专业开发人员懂得一门编程语言就够了?!呵呵,就像其他工作一样,光会一个技能那是远远不够的。如果你想要成为
- java web开发 高并发处理
BreakingBad
javaWeb并发开发处理高
java处理高并发高负载类网站中数据库的设计方法(java教程,java处理大量数据,java高负载数据) 一:高并发高负载类网站关注点之数据库 没错,首先是数据库,这是大多数应用所面临的首个SPOF。尤其是Web2.0的应用,数据库的响应是首先要解决的。 一般来说MySQL是最常用的,可能最初是一个mysql主机,当数据增加到100万以上,那么,MySQL的效能急剧下降。常用的优化措施是M-S(
- mysql批量更新
ekian
mysql
mysql更新优化:
一版的更新的话都是采用update set的方式,但是如果需要批量更新的话,只能for循环的执行更新。或者采用executeBatch的方式,执行更新。无论哪种方式,性能都不见得多好。
三千多条的更新,需要3分多钟。
查询了批量更新的优化,有说replace into的方式,即:
replace into tableName(id,status) values
- 微软BI(3)
18289753290
微软BI SSIS
1)
Q:该列违反了完整性约束错误;已获得 OLE DB 记录。源:“Microsoft SQL Server Native Client 11.0” Hresult: 0x80004005 说明:“不能将值 NULL 插入列 'FZCHID',表 'JRB_EnterpriseCredit.dbo.QYFZCH';列不允许有 Null 值。INSERT 失败。”。
A:一般这类问题的存在是
- Java中的List
g21121
java
List是一个有序的 collection(也称为序列)。此接口的用户可以对列表中每个元素的插入位置进行精确地控制。用户可以根据元素的整数索引(在列表中的位置)访问元素,并搜索列表中的元素。
与 set 不同,列表通常允许重复
- 读书笔记
永夜-极光
读书笔记
1. K是一家加工厂,需要采购原材料,有A,B,C,D 4家供应商,其中A给出的价格最低,性价比最高,那么假如你是这家企业的采购经理,你会如何决策?
传统决策: A:100%订单 B,C,D:0%
&nbs
- centos 安装 Codeblocks
随便小屋
codeblocks
1.安装gcc,需要c和c++两部分,默认安装下,CentOS不安装编译器的,在终端输入以下命令即可yum install gccyum install gcc-c++
2.安装gtk2-devel,因为默认已经安装了正式产品需要的支持库,但是没有安装开发所需要的文档.yum install gtk2*
3. 安装wxGTK
yum search w
- 23种设计模式的形象比喻
aijuans
设计模式
1、ABSTRACT FACTORY—追MM少不了请吃饭了,麦当劳的鸡翅和肯德基的鸡翅都是MM爱吃的东西,虽然口味有所不同,但不管你带MM去麦当劳或肯德基,只管向服务员说“来四个鸡翅”就行了。麦当劳和肯德基就是生产鸡翅的Factory 工厂模式:客户类和工厂类分开。消费者任何时候需要某种产品,只需向工厂请求即可。消费者无须修改就可以接纳新产品。缺点是当产品修改时,工厂类也要做相应的修改。如:
- 开发管理 CheckLists
aoyouzi
开发管理 CheckLists
开发管理 CheckLists(23) -使项目组度过完整的生命周期
开发管理 CheckLists(22) -组织项目资源
开发管理 CheckLists(21) -控制项目的范围开发管理 CheckLists(20) -项目利益相关者责任开发管理 CheckLists(19) -选择合适的团队成员开发管理 CheckLists(18) -敏捷开发 Scrum Master 工作开发管理 C
- js实现切换
百合不是茶
JavaScript栏目切换
js主要功能之一就是实现页面的特效,窗体的切换可以减少页面的大小,被门户网站大量应用思路:
1,先将要显示的设置为display:bisible 否则设为none
2,设置栏目的id ,js获取栏目的id,如果id为Null就设置为显示
3,判断js获取的id名字;再设置是否显示
代码实现:
html代码:
<di
- 周鸿祎在360新员工入职培训上的讲话
bijian1013
感悟项目管理人生职场
这篇文章也是最近偶尔看到的,考虑到原博客发布者可能将其删除等原因,也更方便个人查找,特将原文拷贝再发布的。“学东西是为自己的,不要整天以混的姿态来跟公司博弈,就算是混,我觉得你要是能在混的时间里,收获一些别的有利于人生发展的东西,也是不错的,看你怎么把握了”,看了之后,对这句话记忆犹新。 &
- 前端Web开发的页面效果
Bill_chen
htmlWebMicrosoft
1.IE6下png图片的透明显示:
<img src="图片地址" border="0" style="Filter.Alpha(Opacity)=数值(100),style=数值(3)"/>
或在<head></head>间加一段JS代码让透明png图片正常显示。
2.<li>标
- 【JVM五】老年代垃圾回收:并发标记清理GC(CMS GC)
bit1129
垃圾回收
CMS概述
并发标记清理垃圾回收(Concurrent Mark and Sweep GC)算法的主要目标是在GC过程中,减少暂停用户线程的次数以及在不得不暂停用户线程的请夸功能,尽可能短的暂停用户线程的时间。这对于交互式应用,比如web应用来说,是非常重要的。
CMS垃圾回收针对新生代和老年代采用不同的策略。相比同吞吐量垃圾回收,它要复杂的多。吞吐量垃圾回收在执
- Struts2技术总结
白糖_
struts2
必备jar文件
早在struts2.0.*的时候,struts2的必备jar包需要如下几个:
commons-logging-*.jar Apache旗下commons项目的log日志包
freemarker-*.jar
- Jquery easyui layout应用注意事项
bozch
jquery浏览器easyuilayout
在jquery easyui中提供了easyui-layout布局,他的布局比较局限,类似java中GUI的border布局。下面对其使用注意事项作简要介绍:
如果在现有的工程中前台界面均应用了jquery easyui,那么在布局的时候最好应用jquery eaysui的layout布局,否则在表单页面(编辑、查看、添加等等)在不同的浏览器会出
- java-拷贝特殊链表:有一个特殊的链表,其中每个节点不但有指向下一个节点的指针pNext,还有一个指向链表中任意节点的指针pRand,如何拷贝这个特殊链表?
bylijinnan
java
public class CopySpecialLinkedList {
/**
* 题目:有一个特殊的链表,其中每个节点不但有指向下一个节点的指针pNext,还有一个指向链表中任意节点的指针pRand,如何拷贝这个特殊链表?
拷贝pNext指针非常容易,所以题目的难点是如何拷贝pRand指针。
假设原来链表为A1 -> A2 ->... -> An,新拷贝
- color
Chen.H
JavaScripthtmlcss
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd"> <HTML> <HEAD>&nbs
- [信息与战争]移动通讯与网络
comsci
网络
两个坚持:手机的电池必须可以取下来
光纤不能够入户,只能够到楼宇
建议大家找这本书看看:<&
- oracle flashback query(闪回查询)
daizj
oracleflashback queryflashback table
在Oracle 10g中,Flash back家族分为以下成员:
Flashback Database
Flashback Drop
Flashback Table
Flashback Query(分Flashback Query,Flashback Version Query,Flashback Transaction Query)
下面介绍一下Flashback Drop 和Flas
- zeus持久层DAO单元测试
deng520159
单元测试
zeus代码测试正紧张进行中,但由于工作比较忙,但速度比较慢.现在已经完成读写分离单元测试了,现在把几种情况单元测试的例子发出来,希望有人能进出意见,让它走下去.
本文是zeus的dao单元测试:
1.单元测试直接上代码
package com.dengliang.zeus.webdemo.test;
import org.junit.Test;
import o
- C语言学习三printf函数和scanf函数学习
dcj3sjt126com
cprintfscanflanguage
printf函数
/*
2013年3月10日20:42:32
地点:北京潘家园
功能:
目的:
测试%x %X %#x %#X的用法
*/
# include <stdio.h>
int main(void)
{
printf("哈哈!\n"); // \n表示换行
int i = 10;
printf
- 那你为什么小时候不好好读书?
dcj3sjt126com
life
dady, 我今天捡到了十块钱, 不过我还给那个人了
good girl! 那个人有没有和你讲thank you啊
没有啦....他拉我的耳朵我才把钱还给他的, 他哪里会和我讲thank you
爸爸, 如果地上有一张5块一张10块你拿哪一张呢....
当然是拿十块的咯...
爸爸你很笨的, 你不会两张都拿
爸爸为什么上个月那个人来跟你讨钱, 你告诉他没
- iptables开放端口
Fanyucai
linuxiptables端口
1,找到配置文件
vi /etc/sysconfig/iptables
2,添加端口开放,增加一行,开放18081端口
-A INPUT -m state --state NEW -m tcp -p tcp --dport 18081 -j ACCEPT
3,保存
ESC
:wq!
4,重启服务
service iptables
- Ehcache(05)——缓存的查询
234390216
排序ehcache统计query
缓存的查询
目录
1. 使Cache可查询
1.1 基于Xml配置
1.2 基于代码的配置
2 指定可搜索的属性
2.1 可查询属性类型
2.2 &
- 通过hashset找到数组中重复的元素
jackyrong
hashset
如何在hashset中快速找到重复的元素呢?方法很多,下面是其中一个办法:
int[] array = {1,1,2,3,4,5,6,7,8,8};
Set<Integer> set = new HashSet<Integer>();
for(int i = 0
- 使用ajax和window.history.pushState无刷新改变页面内容和地址栏URL
lanrikey
history
后退时关闭当前页面
<script type="text/javascript">
jQuery(document).ready(function ($) {
if (window.history && window.history.pushState) {
- 应用程序的通信成本
netkiller.github.com
虚拟机应用服务器陈景峰netkillerneo
应用程序的通信成本
什么是通信
一个程序中两个以上功能相互传递信号或数据叫做通信。
什么是成本
这是是指时间成本与空间成本。 时间就是传递数据所花费的时间。空间是指传递过程耗费容量大小。
都有哪些通信方式
全局变量
线程间通信
共享内存
共享文件
管道
Socket
硬件(串口,USB) 等等
全局变量
全局变量是成本最低通信方法,通过设置
- 一维数组与二维数组的声明与定义
恋洁e生
二维数组一维数组定义声明初始化
/** * */ package test20111005; /** * @author FlyingFire * @date:2011-11-18 上午04:33:36 * @author :代码整理 * @introduce :一维数组与二维数组的初始化 *summary: */ public c
- Spring Mybatis独立事务配置
toknowme
mybatis
在项目中有很多地方会使用到独立事务,下面以获取主键为例
(1)修改配置文件spring-mybatis.xml <!-- 开启事务支持 --> <tx:annotation-driven transaction-manager="transactionManager" /> &n
- 更新Anadroid SDK Tooks之后,Eclipse提示No update were found
xp9802
eclipse
使用Android SDK Manager 更新了Anadroid SDK Tooks 之后,
打开eclipse提示 This Android SDK requires Android Developer Toolkit version 23.0.0 or above, 点击Check for Updates
检测一会后提示 No update were found