数据结构--二叉堆、d堆、左式堆和斜堆
本文是转载,出自:http://blog.csdn.net/yangtrees/article/details/8252760点击打开链接
实现优先队列结构主要是通过堆完成,主要有:二叉堆、d堆、左式堆、斜堆、二项堆、斐波那契堆、pairing 堆等。
1. 二叉堆
1.1. 定义
完全二叉树,根最小。
存储时使用层序。
1.2. 操作
(1). insert(上滤)
插入末尾 26,不断向上比较,大于26则交换位置,小于则停止。
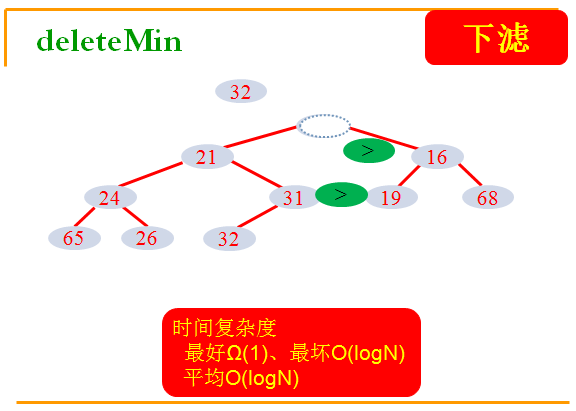
(2). deleteMin(下滤)
提取末尾元素,放在堆顶,不断下滤:
(3). 其他操作:
都是基于insert(上滤)与deleteMin(下滤)的操作。
减小元素:减小节点的值,上滤调整堆。
增大元素:增加节点的值,下滤调整堆。
删除非顶点节点:直接删除会出问题。方法:减小元素的值到无穷小,上滤后删除。
Merge:insert one by one
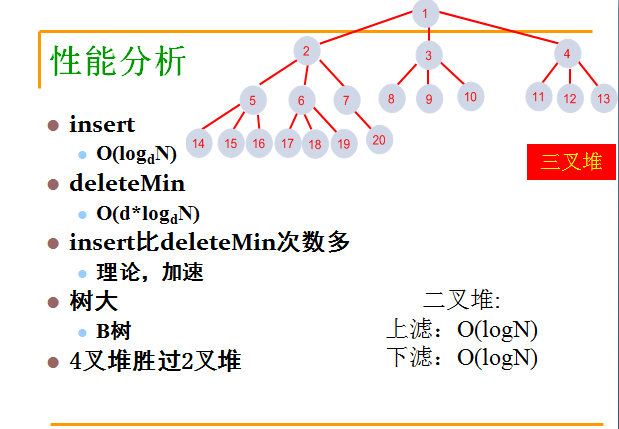
2. d叉堆
2.1. 定义
完全d叉树,根最小。
存储时使用层序。
2.2. 操作:
操作跟二叉堆基本一致:insert,deleteMin,增大元素,减小元素,删除非顶元素,merge。
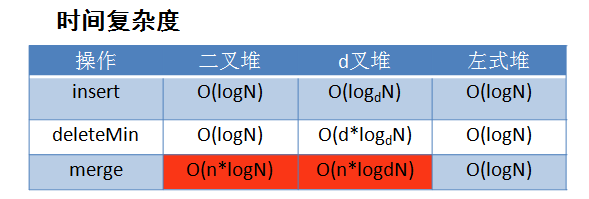
2.3 二叉堆与d叉堆的对比:
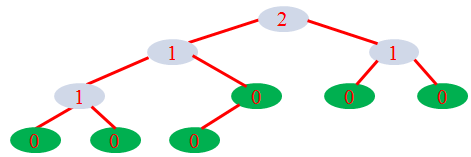
3. 左式堆
3.1. 定义
3.2. 操作:
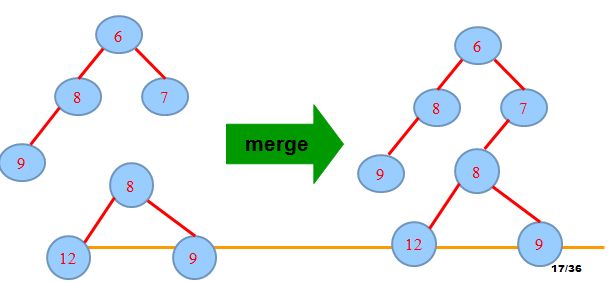
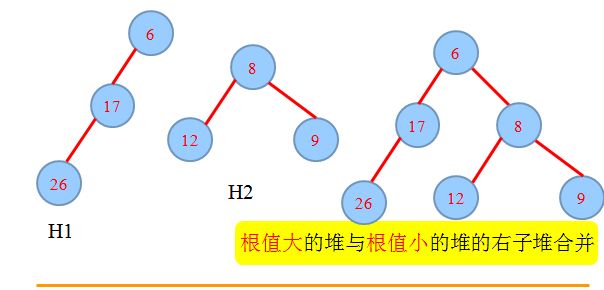
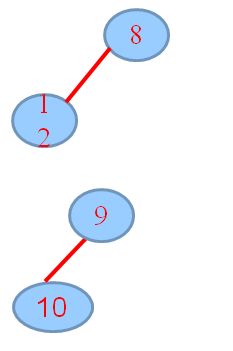
(1) merge :
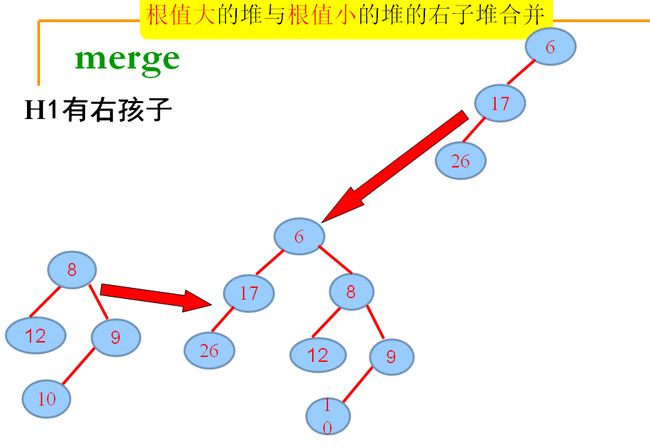
(1.3).H1根有右孩子
1.初始状态,H1的根6,H2的根为8,将H2合并到H1。
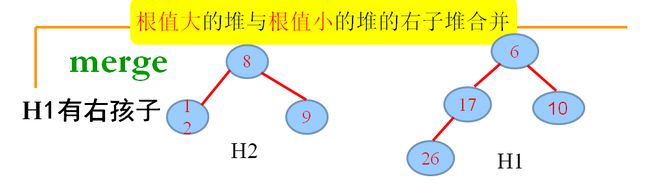
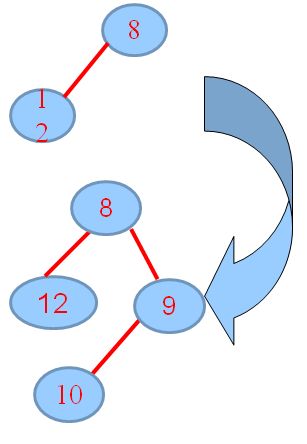
2.将H1构造成根无右孩子的形式:
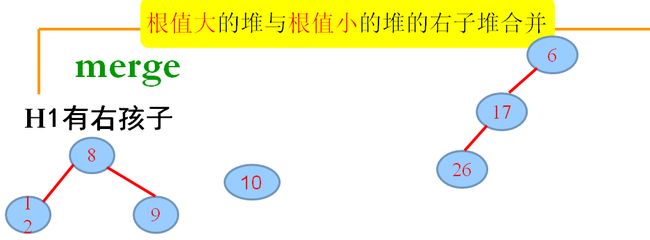
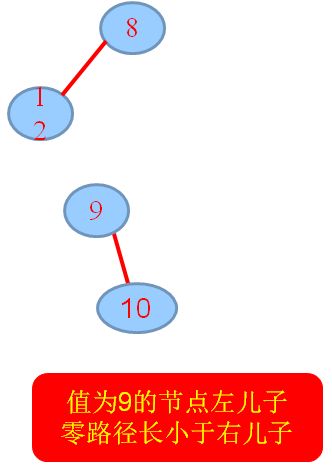
3.将元素10, merge到H2,要首先将H2构造成根无右孩子的形式,递归,merge,若出现不满足:零路径长:左儿子≧右儿子,交换左右孩子……
4.
5.
3.3. 性质分析:
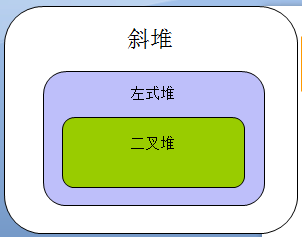
4. 斜堆
4.1. 定义
4.2性能比较:
5. 总结
如果是不支持所谓的合并操作union的话,普通的堆数据结构就是一种很理想的数据结构(堆排序)。 但是如果想要支持集合上的合并操作的话,最好是使用二项堆或者是斐波那契堆,普通的堆在union操作上最差的情况是O(n),但是二项堆和斐波那契堆是O(lgn)。
Binary heap Binomial heap Fibonacci heap
二叉堆(最坏情况) 二项堆(最坏情况)(斐波那契堆(平摊))
Procedure (worst-case) (worst-case) (amortized)
--------------------------------------------------------------
MAKE-HEAP (1) (1) (1)
INSERT (lg n) O(lg n) (1)
MINIMUM (1) O(lg n) (l)
EXTRACT-MIN (lg n) (1g n) O(lg n)
UNION (n) O(lg n) (1)
DECREASE-KEY (lg n) (lg n) (1)
DELETE (1g n) (lg n) O(lg n)