【Modern OpenGL】光照基础 Basic Lighting

说明：跟着learnopengl的内容学习，不是纯翻译，只是自己整理记录。
强烈推荐原文，无论是内容还是排版。 原文链接
本文地址：http://blog.csdn.net/aganlengzi/article/details/50479605

光照基础 Basic Lighting

真实世界中的光照是十分复杂的，需要依赖太多的因素，有时候甚至我们有限的处理器资源都无法完成计算。因此，OpenGL中的光照模型是真实世界中的一种简化的模拟和近似。但是其基本的原理是一致的。其中一种是phong光照模型。它包含三个主要的部分：环境光、漫反射光和镜面反射光。从下面的图中我们可以先直观地感受一下这三种光和它们的作用效果：

• 环境光：即使在全黑的空间中，比如晚上关了灯的房间中，也会有一些别处的光照射在物体上：比如说远处的路灯光，月光等等。所以在这个空间中的物体并不会是完全黑色的。phong光照模型中通过环境光来模拟这种情况，它的作用效果是物体总不会完全变成黑色而让人看不见。

• 漫反射光：模拟了真实世界中的光的漫反射（照射在物体上的光向四面八方反射）。这是一个对象可见的最重要的部分。它的作用效果是面向光源一侧的表面要比其它侧面亮。

• 镜面反射光：模拟的是点状光源照射在物体上的情形（比如说手电筒照射在镜面上）。镜面反射光表现出来的效果更多是光源的颜色而不是物体的颜色。

为了能够在后面的教程中创建出接近真实光照和颜色的场景，我们至少需要使用以上这三种光分量。我们将从最简单的一个环境光来开始我们对phong光照模型中的这三种光源进行学习。

环境光 Ambient lighting

光源通常不会只有一个，而是有好多，虽然它们可能不是那么明显就能被看见。光的一个属性是它能够沿着不同的方向传输并且能够进行反射。而被反射的光又成为了一种间接的光源作用在其它物体上。把上面的过程考虑进去的算法称作全局照明算法，但是它的计算代价太大太复杂而不实用。

对于我们来说，并不需要那么精确的表示，所以我们只需要实用一种简化的全局光照模型就可以了，这就是环境光。正如你在上一次教程中使用全局颜色将物体着色使它们看上去总是有周围有相同颜色的光源对它们照明一样。

在场景中添加环境光是十分简单的。我们只需要设定一种环境光的颜色，并且将这个颜色值和一个环境光因子常量相乘，然后再将得到的结果作用在对象上就可以了（也就是将对象的每个片段都加以环境光作用就可以了），你一定已经想到了怎么作用到我们创建的对象上——只需要在片段处理器中进行相乘操作就可以了。就像下面这样：

void main()
{
    float ambientStrength = 0.1f;
    vec3 ambient = ambientStrength * lightColor;

    vec3 result = ambient * objectColor;
    color = vec4(result, 1.0f);
}  

现在如果你运行你的程序，应该会感觉到你创建的物体上已经着了环境光了。具体的效果是这个物体显得比较暗，但是又不是全黑色（没有颜色），像下图中显示的那样（好吧，确实不是太好看）：

注意，因为我们并没有对立方体光源的fragment shader做任何操作，所以立方体光源是不受影响的，这也正是我们在前面就把它们两个的shader程序分开的目的，不是吗。

漫反射光 Diffuse lighting

只有环境光的场景看上去并不是很真实。但是只要为场景添加了漫反射光，场景中物体的真实性会立马大幅度增加。漫反射光使得越靠近光源的表面越亮。为了能让你有一个更加直观的认识，看下图：

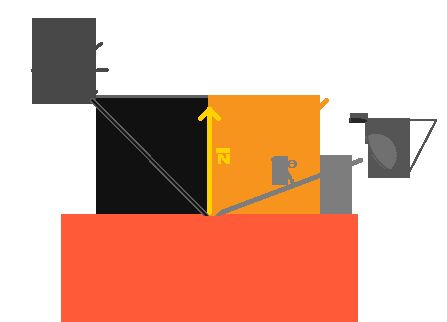
在上图中，我们看到的是左侧有一个光源，它发出的一条光线照射在了物体的一个点上，关于这个点的所有颜色数据就是片段处理器需要处理的一个片段（fragment）。不同的照射角度对点的作用效果不同，垂直照射使得光源对物体上点的作用最大。为了测量光线对这个点的作用角度，我们借助图中的黄色线，称作法向量。法向量定义为某点出垂直于这个点所在平面的有向线段。我们后面会用到法向量。光线与法向量之间的角度可以通过两个向量的点乘轻松得到。

向量之间的角度（0-90）越小，相乘得到的模值越大。假设两个单位向量之间的角度是0度，那么它们相乘得到的向量的长度就是1，如果角度是90度，那么它们相乘得到的向量长度就是0。这个结果和图中所示的θ是一致的：当光线和某点的法向量之间的夹角是90度，那么光线对这个点的作用就是0，但是如果光线和法向量之间的夹角是0度，那么光线对这个点的作用就是最大。

需要注意的是：在计算中，我们只想得到这两个向量之间的夹角的余弦值，这就需要将这两个向量进行标准化，也就是把这两个向量的模变为1，变成单位向量。否则计算得到的就不是夹角的余弦值。

两个单位向量之间的点乘得到的是一个缩放因子，它代表了光线对某个点的作用强度值。而这个强度值因子取决于光线与特定点的法向量的角度。

那么，有了上面所说的法向量和光线之间夹角的余弦值，我们应该怎样计算漫反射光呢？

法向量 Normal vectors

前面说过，点的法向量是处置以点所在平面的一个单位向量。对于复杂的对象表明，我们可以通过叉乘的方式得到这个向量。但是我们使用的立方体并不是一个复杂的对象，所以我们实际上可以手工来为立方体添加法向量（立方体有六个面，每个面上所有的点的法向量是相同的）。所以只需要为每个面添加一个相同的法向量就可以了。因为我们在绘制立方体的时候是按照12个三角形的方式绘制的，这样就形成了最终的立方体顶点数据。

我们再一次修改了顶点数据数组，相应的改变需要在代码中体现。首先需要更改顶点处理程序。

#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
...

其次，还应该告诉OpenGL应该怎样解读我们的数据，也就是修改glVertexAttribPointer函数的参数。另外，需要注意的是，我们的立方体光源和立方体对象使用的是同一个顶点数据。但是绘制立方体光源的顶点处理程序和片段处理程序并没有更新，我们也不需要更新它们。但是我们需要告诉OpenGL在绘制立方体光源的时候使用的数据只是顶点数据。

glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(GLfloat), (GLvoid*)0);
glEnableVertexAttribArray(0);

具体的做法是，我们只需要将原来的3个GLfloat类型的步长改成6个GLfloat步长。这样做是高效的，因为相比于再创建一个VBO来保存我们对象的数据，这种做法节省了GPU显存。

所有的光照计算都是在片段处理器中完成的，所以我们还需要将传递进去的法向量数据从顶点处理器中传递到片段处理器汇总。我们通过之前讲过的in和out变量完成这个操作，即在顶点处理程序中定义输出类型out变量vec3 Normal：

out vec3 Normal

void main()
{
    gl_Position = projection * view * model * vec4(position, 1.0f);
    Normal = normal;
} 

然后在片段处理程序中定义相同类型的但是是输入类型in的变量就可以了：

in vec3 Normal;  

计算漫反射光 Calculating the diffuse color

现在，我们有了立方体表面所有点的法向量，但是我们还需要得到光源的位置向量和片段的位置向量（以便得到光线的单位向量而最终得到夹角的余弦值）。因为光源的位置是一个静止不变的值，所以我们可以将其设置为片段处理程序中的一个uniform类型的变量：

uniform vec3 lightPos;  

别忘了在程序中更新这个uniform类型的变量（在game loop内部还是外部都是可以的，因为它是不变的）。我们声明lightPos变量来表示光源的位置，就像前面教程中的做法一样：

GLint lightPosLoc = glGetUniformLocation(lightingShader.Program, "lightPos");
glUniform3f(lightPosLoc, lightPos.x, lightPos.y, lightPos.z); 

然后我们需要的是片段（点）的位置。我们不是已经有了点的位置了吗？是的，但是我们需要在世界坐标系中完成光照计算，所以我们的顶点位置也应该是设置在世界坐标系中的。我们通过将点的位置属性和模型矩阵相乘的方式把点的位置转换到世界坐标系中。者在顶点处理程序中可以十分方便地完成：

out vec3 FragPos;  
out vec3 Normal;

void main()
{
    gl_Position = projection * view * model * vec4(position, 1.0f);
    FragPos = vec3(model * vec4(position, 1.0f));
    Normal = normal;
}

和上面传递法向量一样，需要在片段处理程序中声明用于参数传递的变量：

in vec3 FragPos;  

现在，万事具备，只欠计算了。计算当然是在片段处理程序中完成。

首先，我们先计算得到光线的单位方向向量。我们知道光线的方向向量就是物体上的点的位置向量和光源的位置向量之差。所以计算方式就是分简单了。需要注意的是，我们在计算过程中和计算的结果需要是单位向量，所以具体的操作是：

vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos);  

在计算光照时，我们通常并不关系向量的大小（长度）我们只关系它们的方向，因为我们需要的是它们讷的方向。这也简化了很多计算，比如只通过单位向量之间的点乘就能够得到它们之间夹角的余弦值。所以在进行光照计算的时候我们应该时刻注意计算得到单位向量。

接下来就是计算光线对某个点的强度值了。像上面说的那样我们只需要计算两个单位向量（法向量和光线方向）之间点乘的结果就能够得到光线对这个点的光照强度。这个光照强度和之前设置的光源颜色值之间的乘积就是对应的漫反射光的作用效果了：

float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;

需要注意的是，如果两个向量之间的夹角大于90度，那么点乘的结果就是一个负值。那么我们会得到一个负值的漫反射效果。因此，我们对两个向量之间的点乘结果加了一个判断。如果得到的结果是负值，我们就将结果赋值为0.0。

现在我们的场景中有了两种光了：环境光和漫反射光。我们需要把它们都作用到我们最终生成的显示在屏幕上的像素点上，也就是左乘：

vec3 result = (ambient + diffuse) * objectColor;
color = vec4(result, 1.0f);

如果你的程序运行正确的话应该得到的效果和我的差不多：

从上面的效果图中，你可以看到，当添加了漫反射光，这个立方体看上去更加真实了一些。虽然角度没有调整好，在后面加上旋转什么的操作再看吧。这是目前的main.cpp和shader.vs以及shader.frag。

镜面反射光 Specular Lighting

下面我们来看一下镜面反射光，它是phong光照模型中我们要讲的最后一个光源了。

像漫反射光一样，镜面反射光也是需要根据光线的方向向量和物体的法向量计算出来的，但是镜面反射光还需要依赖视觉方向，比如说：观察者从哪个方向来观察我们要计算的点。如果我们把物体的表面想象成一个镜面，镜面反射光就是我们从某个位置看到的情况。如下图所示：

像图中展示的一样，为了计算我们看到的镜面光强度，我们需要首先根据入射光线和法线计算出光线的出射方向，出射方向和观察方向之间的夹角决定了我们能够看到的反射光的强度。这个角度越小，我们能够看到的镜面反射光的强度就越强。镜面反射光的作用效果就是我们能够在我们视线和光线在物体表面的交点处看到曝光的一团的样子，相信在实际的生活中，我们都是经历过这样的情形的。

相比于漫反射光的计算，这个视线向量是我们为了计算镜面反射光需要额外计算得到的一个量。这视线向量的计算实际上是比较简单的：我们可以通过观察点位置和物体表面特定点的位置计算得到。得到了这个视线向量和物体表面点的法向量以及入射光线的单位向量我们就可以计算上述角度的余弦值，这就是镜面反射光的光强度。然后将光强度和光源的颜色值进行相乘便得到了镜面反射光的作用效果。把镜面反射光的作用效果加到环境光和漫反射光上面便得到了最终phong光照模型下整体的作用效果。

我们选择在世界坐标系中完成光照计算，但是大部分人更希望在观察坐标系中完成计算。在观察坐标系中计算的一大好处是观察者的的位置始终是在（0,0,0）处的，所以我们很容易就能确定计算镜面反射光需要的观察者位置坐标。但是在世界坐标系中进行光照计算是十分有利于学习和理解的。所以在教程中选择的是在世界坐标系中进行光照计算。

为了得到观察者的位置坐标，我们简单地利用摄像机位置作为观察者位置坐标。这个值是我们在OpenGL代码中设定的一个位置向量。好了，这个值已经得到，让我们在片段处理程序中添加一个uniform类型的变量来传递这个值到片段处理程序中，如下所示：

uniform vec3 viewPos;
...
GLint viewPosLoc = glGetUniformLocation(lightingShader.Program, "viewPos");
glUniform3f(viewPosLoc, camera.Position.x, camera.Position.y, camera.Position.z);  

那么现在我们又到了万事具备，只欠计算的时候了。那就开始计算吧！首先我们让我们来设置一下镜面反射光的光照强度为0.5，不设置到100%以防亮瞎我们的眼：

float specularStrength = 0.5f;

如果我们将这个值设置为1.0f，我们得到的镜面反射光的效果将会太明显。在这个教程中我们先设置它为0.5，在下个教程汇总我们将会讨论如何正确设置光照强度和光照对物体的作用效果。好了，现在让我们真正开始利用上面准备好的各个量来进行镜面反射光照强度的计算吧：

vec3 viewDir = normalize(viewPos - FragPos);
vec3 reflectDir = reflect(-lightDir, norm); 

需要注意的是，我们在上面的代码中对光线方向lightDir进行了反向操作。因为reflect函数的第一个参数是指从光源指向作用点的光线方向，但是在前面的计算中，我们计算光线方向的方法是光源的位置减去物体表面点的位置，方向向量指向的是你被减数，所以正好和要求的是相反的方向，所以这里进行反向操作。

然后我们通过下面的公式计算镜面反射光的光照强度：

float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;  

如上面的代码所示，我们首先将视线向量和反射向量做点乘，并且像计算漫反射光一样保证得到的结果值非负。并且我们将得到的值做一个32次幂，这个32是物体的反射系数，反射系数越高的物体反射能力越强，计算得到的镜面反射光也就越强。下面这张图能够充分帮助你理解这个值的含义，在保证其他变量都相同的情况下，只改变反射系数得到的效果：

我们不想让镜面反射光分量那么显眼，所以我们将这个值设置为32。接下来，我们把镜面反射光和上面已经介绍的两种光结合起来，作用在物体上，得到最终物体的颜色：

vec3 result = (ambient + diffuse + specular) * objectColor;
color = vec4(result, 1.0f);

到这儿，Phong光照模型的三种分量的光源就都计算完成了，我们来看一看成果。我运行的结果是这个样子的：

这里是main.cpp和改过的shader.frag。

在早些时候，开发者经常是在顶点处理程序（vertex shader）中完成光照计算的，在顶点处理程序中完成光照计算的最大好处是开销小。因为顶点处理程序中只有开发者定义的数量的顶点，所以在这儿进行光照计算也就只要对这些顶点进行计算就可以了。但是也正是指针对这些顶点进行光照计算，对象表面的其它顶点的颜色值实际上是通过插值的方法得到的，插值的后果是不真实（除非模型由大量点构成），两种方式的对比图如下所示：

上图中的Gouruad就是Phong光照模型在顶点处理程序中实现的称呼方法。可以看到，Gouruad光照模型和Phong光照模型相比，后者的真实度更高，显得更加平滑。

通过上面Phong光照模型的学习，相信你已经感受到了光照的魔力。在后面的教程中，我们将会更加深入地研究光照模型。