二分图的基本模型思想
（在网上看的博客，因为博主也是转载而且未附上链接，不好意思）
今天突然想到一个关于二分图的灰常xx的比喻，所以赶紧写下来。
假设全班的男生集合为R1，女生集合为R2，男生分别记为m1,m2……女生分别记为w1,w2……。最近全班学生大多数都寂寞了，想谈恋爱了
于是大家都在物色目标。其中有不少男女生互相之间都有好感。但一个男生可能对多个女生有好感，一个女生也可能对多个男生有好感（都是花心大萝卜
)
—————————————————————背景交代完——————————————————————
1.现在知道互相有好感的男女生都有哪些，求最多能在班上撮合几对？
这是一个典型的二分图最大匹配的问题。
2.如果给互相有好感的男女生的好感评一个分，问：撮合之后的分数之和最多是多少？
这貌似是一个二分图的最优匹配的问题。
————————————————下面说一下我理解中的匈牙利算法—————————————————
想撮合最多对数的情侣，首先先把目前单身的尽量撮合成一对（预处理）
然后从某一个人开始，挨个找他（她）喜欢的人，然后从他（她）喜欢的人出发，继续挨个找这个人喜欢的人。我们把这个循环简单的写为M1'—W1‘—M2’—…………。当找到某一个人，发现这个人还是单身，就把之前所有有男女朋友的全部拆散（的确很邪恶）然后再撮合他们和这次寻找的关系链的后一个人在一起。如此若干次后，发现没有拆散恋人再重组能使得单身的人数减少的情况，就是二分图的最大匹配了。
最大匹配与二分图建图概述
一：关于二分图最大匹配的两个定理：
2:二分图的最小覆盖数 = 最大匹配数
3:最小路径覆盖 = 最大独立集
最大独立集是指求一个二分图中最大的一个点集，该点集内的点互不相连。
最小顶点覆盖是指 在二分图中，用最少的点，让所有的边至少和一个点有关联。
最小路径覆盖是指一个不含圈的有向图G中，G的一个路径覆盖是一个其结点不相交的路径集合P，图中的每一个结点仅包含于P中的某一条路径。路径可以从任意结点开始和结束，且长度也为任意值，包括0
关于二分图最大匹配算法：http://blog.csdn.net/no_retreats/article/details/7854091
常见的建图模型：(以下是参照其他资源小结的)
模型一：行列匹配法
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
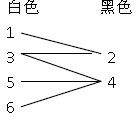
初初看来和二分图是没有什么联系，不过我们可以试试换个角度去思考问题，我们想要杀死敌人是不是只要有箭经过他就行了是吧，也就是说所有的敌人被箭覆盖过就行了。嗯，没错，就是覆盖，最小顶点覆盖。既然我们要杀的是敌人，那么我们的点就应该是敌人的位置，只要有箭经过敌人的位置，那敌人就被我们杀死了有木有。所以我们要依据点来建图，将点的横坐标看成是二分图的X部分，纵坐标看成是二分图的Y部分。由上图可知敌人的位置在（（1,1），（1,3），（2,2），（3,1）），因此我们就用坐标的横纵坐标来见二分图了，其中用边相连的边即为敌人所在的点了。
，一个二分图的最小顶点覆盖就是要找到最少的边把所有的顶点覆盖，正好符合这个题的要求，上面还给出了一个性质，即二分图的最小顶点覆盖是等于二分图的最大匹配。所以我们只需要对上面的那个二分图就最大匹配就行，这样把原本的问题转变的很简单了
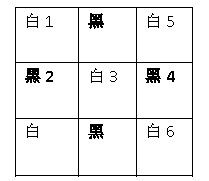
模型二：黑白染色法
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
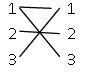
有了这样的思想，我们只需对原图做这样的改动：黑白染色使四周和中间的颜色不同。
然后建图，把相邻的点相连，比如说1和2 2和3 。。。。。。。
