hdu1558

Segment set

Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2728 Accepted Submission(s): 1028

Problem Description

A segment and all segments which are connected with it compose a segment set. The size of a segment set is the number of segments in it. The problem is to find the size of some segment set.

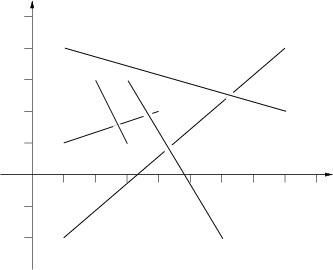
Input

In the first line there is an integer t - the number of test case. For each test case in first line there is an integer n (n<=1000) - the number of commands.

There are two different commands described in different format shown below:

P x1 y1 x2 y2 - paint a segment whose coordinates of the two endpoints are (x1,y1),(x2,y2).
Q k - query the size of the segment set which contains the k-th segment.

k is between 1 and the number of segments in the moment. There is no segment in the plane at first, so the first command is always a P-command.

Output

For each Q-command, output the answer. There is a blank line between test cases.

Sample Input

   
   
   
   

    
    
    
    1
10
P 1.00 1.00 4.00 2.00
P 1.00 -2.00 8.00 4.00
Q 1
P 2.00 3.00 3.00 1.00
Q 1
Q 3
P 1.00 4.00 8.00 2.00
Q 2
P 3.00 3.00 6.00 -2.00
Q 5
   
   
   
   

Sample Output

   
   
   
   

    
    
    
    1
2
2
2
5
   
   
   
   

Author

LL

并查集还好说，主要是线段相交不会做，今后要多多做几何方面的题啊！得用模板才能过的

#include<stdio.h>
#include<stdlib.h>
struct node
{
 double x1,y1,x2,y2;
};
struct node sum[1001];
int nume[1001];
 

double ji(double x1,double y1,double x2,double y2,double x0,double y0)
{
 return (y0-y1)*(x2-x1)-(y2-y1)*(x0-x1);
}
int charge(int n,int i)
{
 double a,b,c,d;
  a=ji(sum[i].x1,sum[i].y1,sum[i].x2,sum[i].y2,sum[n].x1,sum[n].y1);
  b=ji(sum[i].x1,sum[i].y1,sum[i].x2,sum[i].y2,sum[n].x2,sum[n].y2);
  c=ji(sum[n].x1,sum[n].y1,sum[n].x2,sum[n].y2,sum[i].x1,sum[i].y1);
  d=ji(sum[n].x1,sum[n].y1,sum[n].x2,sum[n].y2,sum[i].x2,sum[i].y2);
  if(a*b<=0&&c*d<=0)
   return i+1;
  return 0;
}
//判断线段是否相交  计算公式不会证明  不过是自己猜想出来的
int find(int x)
{
 if(nume[x]!=x)
  nume[x]=find(nume[x]);
 return nume[x];
}
void merge(int a,int b)
{
 int x,y;
 x=find(a);
 y=find(b);
 if(x>y)
  nume[x]=y;
 else
  nume[y]=x;
}
//并查集
int main()
{
 int n,l,i,j,t,count,m,x,k,o,y;
 double a1,a2,a3,a4;
 char c;
 scanf("%d",&t);
 for(y=0;y<t;y++)
 {
  scanf("%d",&n);
  for(i=1;i<=n;i++)
     nume[i]=i;
  i=0;
  l=0;
  while(n--)
  {
   getchar();
   scanf("%c",&c);
   if(c=='P')
   {
    scanf("%lf%lf%lf%lf",&a1,&a2,&a3,&a4);
    if(a1<a3)
    {
     sum[i].x1=a1;
     sum[i].y1=a2;
     sum[i].x2=a3;
     sum[i].y2=a4;
    }
    else
    {
     sum[i].x1=a3;
     sum[i].y1=a4;
     sum[i].x2=a1;
     sum[i].y2=a2;
    }
    for(k=0;k<l;k++)
    {
     m=charge(i,k);
     if(m!=0)
         merge(m,l+1);
    }
    i++;
    l++;
   }
   else
   {
    count=0;
    scanf("%d",&x);
    while(nume[x]!=x)
     x=nume[x];
    for(j=1;j<=l;j++)
    {
     o=j;
     while(nume[o]!=o)
      o=nume[o];
     if(o==x)
      count++;
    }
    printf("%d\n",count);
   }
  }
  if(y<t-1)
     printf("\n");
 }
 return 0;
}