树链剖分

原文链接：

http://blog.csdn.net/dyx404514/article/details/8718249

http://blog.sina.com.cn/s/blog_7a1746820100wp67.html

前段时间学习了下树链剖分，好久没看了，今天又复习一遍，赶紧写下来，别又忘了。

我们在信息学竞赛中，有时会碰到这么一类题型，在一棵树中，修改两点之间路径上的所有边（或点）上的某个变量（如边的长度，点的权值等等），然后询问单个点（或边）或者两点之间路径上的所有点（或边）的某些性质（如边权之和，最大边最小边等等）。对于这样的题，往往容易往线段树上去靠，但是，单单是用线段树是无法维护每一条链的性质的，所以我们需要一种算法将树链分开来，使得每条链可以和线段树中的一个区间一一对应上。(当然树链剖分远远不止这些简单的应用，也不一定要和线段树有什么关系，总之就是将树链剖分开来吧)。

树链剖分有很多种剖分方法，最常用的应该就是轻重边剖分了吧（在网上大部分介绍的都是这种剖分方法），什么是轻重边剖分呢？

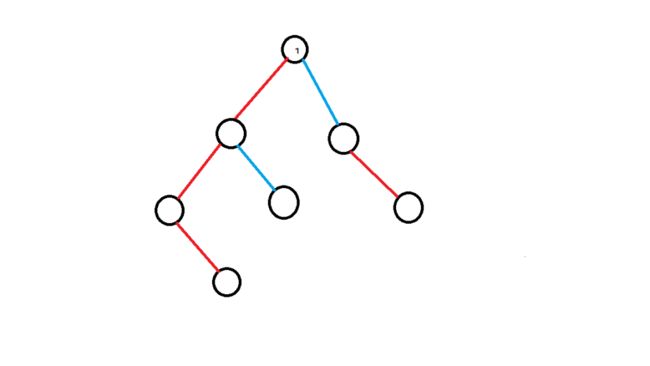
我们首先将树中的边分为两部分，轻边和重边，记size(U)为以U为根的子树的节点的个数，令V为U的儿子中size最大的一个（如有多个最大，只取一个），则我们说边（U，V）为重边，其余的边为轻边（如下图所示红色为重边，蓝色为轻边）。

我们将一棵树的所有边按上述方法分成轻边和重边后，我们可以得到以下几个性质：

1：若（U,V）为轻边，则size(V)<=size(U)/2。

这是显然的。

2：从根到某一点的路径上轻边的个数不会超过O（logN），（N为节点总数）。

这也是很简单，因为假设从跟root到v的路径有k条轻边，它们是 root->...->v1->...->v2->......->vk->...->v，我们设size(v)=num，显然num>=1,则由性质1，我们有size(Vk)>=2,size(Vk-1)>=4......size(v1)>=2^k，显然有2^k<=N,所以k<=log2(N)。

如果我们把一条链中的连续重边连起来，成为重链，则一条链就变成了轻边与重链交替分段的链，且段数是log(N)级别的，则我们可以讲重链放在线段树中维护，轻边可放可不放，为了方便我一般还是放，但是速度就会打一点折扣了。思路就是这么多，接下来就是具体实现了。

我们需要维护一下值：

siz[v]表示以v为根的子树的节点总数。

dep[v]表示v的深度。

son[v]表示与v在同一重链上的v的儿子节点。

fa[v]表示v的父亲节点。

top[v]表示v所在链的顶端节点。

w[v]表示节点v在线段树中的位置。

siz[],son[],fa[],dep[]可以在第一遍dfs中求出来，top[]，w[]可在第二遍dfs中求出来。具体过程看代码吧。

 算法实现：
    我们可以用两个dfs来求出fa、dep、siz、son、top、w。
    dfs_1：把fa、dep、siz、son求出来，比较简单，略过。
    dfs_2：⒈对于v，当son[v]存在（即v不是叶子节点）时，显然有top[son[v]] = top[v]。线段树中，v的重边应当在v的父边的后面，记w[son[v]] = totw+1，totw表示最后加入的一条边在线段树中的位置。此时，为了使一条重链各边在线段树中连续分布，应当进行dfs_2(son[v])；
           ⒉对于v的各个轻儿子u，显然有top[u] = u，并且w[u] = totw+1，进行dfs_2过程。
           这就求出了top和w。
    将树中各边的权值在线段树中更新，建链和建线段树的过程就完成了。

 struct edge
 {
     int to;
     int next;
 }e[maxn<<1];
 int box[maxn],cnt,tot;
 int siz[maxn],top[maxn],son[maxn],dep[maxn],fa[maxn];
 void init()
 {
     tot=0;
     son[0]=dep[0]=0;
     memset(box,-1,sizeof(box));
     cnt=0;
 }
 void add(int from,int to)
 {
     e[cnt].to=to;
     e[cnt].next=box[from];
     box[from]=cnt++;
 }
 void dfs(int now,int pre)
 {
     siz[now]=1;
     fa[now]=pre;
     son[now]=0;
     dep[now]=dep[pre]+1;
     int t,v;
     for(t=box[now];t+1;t=e[t].next)
     {
         v=e[t].to;
         if(v!=pre)
         {
             dfs(v,now);
             siz[now]+=siz[v];
             if(siz[son[now]]<siz[v])
             {
                 son[now]=v;
             }
         }
     }
 }
 void dfs2(int now,int tp)
 {
     top[now]=tp;
     if(son[now])
     dfs2(son[now],top[now]);
     int t,v;
     for(t=box[now];t+1;t=e[t].next)
     {
         v=e[t].to;
         if(v!=fa[now]&&v!=son[now])
         dfs2(v,v);
     }
 }