字符串的排列组合问题

题目：输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符串abc，则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。 
分析：这是一道很好的考查对递归理解的编程题，因此在过去一年中频繁出现在各大公司的面试、笔试题中。


我们以三个字符abc为例来分析一下求字符串排列的过程。首先我们固定第一个字符a，求后面两个字符bc的排列。当两个字符bc的排列求好之后，我们把第一个字符a和后面的b交换，得到bac，接着我们固定第一个字符b，求后面两个字符ac的排列。现在是把c放到第一位置的时候了。记住前面我们已经把原先的第一个字符a和后面的b做了交换，为了保证这次c仍然是和原先处在第一位置的a交换，我们在拿c和第一个字符交换之前，先要把b和a交换回来。在交换b和a之后，再拿c和处在第一位置的a进行交换，得到cba。我们再次固定第一个字符c，求后面两个字符b、a的排列。


既然我们已经知道怎么求三个字符的排列，那么固定第一个字符之后求后面两个字符的排列，就是典型的递归思路了。


基于前面的分析，我们可以得到如下的参考代码：


void Permutation(char* pStr, char* pBegin);


/////////////////////////////////////////////////////////////////////////
// Get the permutation of a string, 
// for example, input string abc, its permutation is 
// abc acb bac bca cba cab
/////////////////////////////////////////////////////////////////////////
void Permutation(char* pStr)
{
      Permutation(pStr, pStr);
}


/////////////////////////////////////////////////////////////////////////
// Print the permutation of a string, 
// Input: pStr   - input string
//        pBegin - points to the begin char of string 
//                 which we want to permutate in this recursion
/////////////////////////////////////////////////////////////////////////
void Permutation(char* pStr, char* pBegin)
{
      if(!pStr || !pBegin)
            return;


      // if pBegin points to the end of string,
      // this round of permutation is finished, 
      // print the permuted string
      if(*pBegin == '/0')
      {
            printf("%s/n", pStr);
      }
      // otherwise, permute string
      else
      {
            for(char* pCh = pBegin; *pCh != '/0'; ++ pCh)
            {
                  // swap pCh and pBegin
                  char temp = *pCh;
                  *pCh = *pBegin;
                  *pBegin = temp;


                  Permutation(pStr, pBegin + 1);


                  // restore pCh and pBegin
                  temp = *pCh;
                  *pCh = *pBegin;
                  *pBegin = temp;
            }
      }
}


扩展1：如果不是求字符的所有排列，而是求字符的所有组合，应该怎么办呢？当输入的字符串中含有相同的字符串时，相同的字符交换位置是不同的排列，但是同一个组合。举个例子，如果输入aaa，那么它的排列是6个aaa，但对应的组合只有一个。


扩展2：输入一个含有8个数字的数组，判断有没有可能把这8个数字分别放到正方体的8个顶点上，使得正方体上三组相对的面上的4个顶点的和相等。

 

http://www.360doc.com/content/12/0328/19/1429048_198701158.shtml

http://blog.sina.com.cn/s/blog_830cba8a0100wbac.html

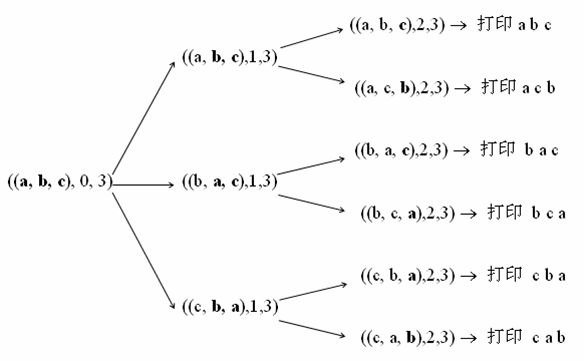
  思路：这是个递归求解的问题。递归算法有四个特性：（1)必须有可达到的终止条件，否则程序将陷入死循环；（2）子问题在规模上比原问题小；（3）子问题可通过再次递归调用求解；（4）子问题的解应能组合成整个问题的解。

    对于字符串的排列问题。如果能生成n - 1个元素的全排列，就能生成n个元素的全排列。对于只有1个元素的集合，可以直接生成全排列。全排列的递归终止条件很明确，只有1个元素时。下面这个图很清楚的给出了递归的过程。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
void f(char *str, int len, int n)
{    
       int i;    
       char tmp;    
       char *p = (char *)malloc(sizeof(*str));    
       if(n==len-1){                                     //只剩一个元素
               printf("%s\n",str);                 //打印
       }else{    
               for(i=n;i<len;i++){    
                        strcpy(p,str);    

                       tmp = *(str+n);                 //交换两个字符
                       *(str+n) = *(str+i);    
                       *(str+i) = tmp;    

                       f(str,len,n+1);    
                       strcpy(str,p);                     //恢复
               }    
       }    
       free(p);    
}    

int main(int argc, char **argv)
{    
       char str[] = "abc";    
       f(str,3,0);    
        
       return 0;    
}