HDU 1988 & ZOJ 2991 Flipping Burned Pancakes(数学啊+模拟)
题目链接:
HDU:http://acm.hdu.edu.cn/showproblem.php?pid=1988
ZOJ:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1990
Problem Description
The cook at the Frobbozz Magic Pancake House sometimes falls asleep on the job while cooking pancakes. As a result, one side of a stack of pancakes is often burned. Clearly, it is bad business to serve visibly burned pancakes to the patrons. Before serving, the waitress will arrange the stacks of pancakes so that the burned sides are facing down. You must write a program to aid the waitress in stacking the pancakes correctly.
We start with a stack of N pancakes of distinct sizes, each of which is burned on one side. The problem is to convert the stack to one in which the pancakes are in size order with the smallest on the top and the largest on the bottom and burned side down for each pancake. To do this, we are
allowed to flip the top k pancakes over as a unit (so the k-th pancake is now on top and the pancake previously on top is now in the k-th position and the burned side goes from top to bottom and vice versa).
For example (+ indicates burned bottom, - a burned top):
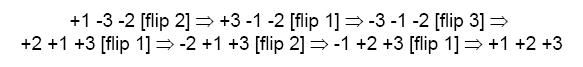
You must write a program which finds a sequence of at most (3n – 2) flips, which converts a given stack of pancakes to a sorted stack with burned sides down.
We start with a stack of N pancakes of distinct sizes, each of which is burned on one side. The problem is to convert the stack to one in which the pancakes are in size order with the smallest on the top and the largest on the bottom and burned side down for each pancake. To do this, we are
allowed to flip the top k pancakes over as a unit (so the k-th pancake is now on top and the pancake previously on top is now in the k-th position and the burned side goes from top to bottom and vice versa).
For example (+ indicates burned bottom, - a burned top):
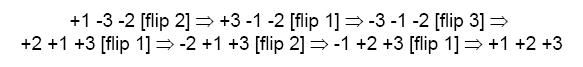
You must write a program which finds a sequence of at most (3n – 2) flips, which converts a given stack of pancakes to a sorted stack with burned sides down.
Input
The first line of the input contains a single decimal integer, N, the number of problem instances to follow. Each of the following N lines gives a separate dataset as a sequence of numbers separated by spaces. The first number on each line gives the number, M, of pancakes in the data set. The remainder of the data set is the numbers 1 through M in some order, each with a plus or minus sign, giving the initial pancake stack. The numbers indicate the relative sizes of the pancakes and the signs indicate whether the burned side is up (-) or down (+). M will be, at most, 30.
Output
For each dataset, you should generate one line of output with the following values: The dataset number as a decimal integer (start counting at one), a space, the number of flips (K, where K >= 0) required to sort the pancakes and a sequence of K numbers, each of which gives the number of pancakes to flip on the corresponding sorting step. There may be several correct solutions for some datasets. For instance 3 2 3 is also a solution to the first problem below.
Sample Input
3 3 +1 -3 -2 4 -3 +1 -2 -4 5 +1 +2 +3 +4 -5
Sample Output
1 6 2 1 3 1 2 1 2 6 4 1 4 3 1 2 3 3 5 1 5
题意:
一共有n块煎饼,面积分别是从1到n,正面朝上为‘+’,反面朝上为‘-’。
每次可以选择上面连续的若干块一起翻转过来。
求翻转的步骤,可以使得最后 正面朝上,面积从上到下是从小到大。
代码如下:
#include <cstdio>
#include <cmath>
int a[47];
void reserve (int pos)
{
int tt;
for(int i = 1, j = pos; i < j; i++,j--)
{
tt = a[i],a[i] = a[j],a[j] = tt;
}
for(int i = 1; i <= pos; i++)
{
a[i] = -a[i];
}
}
int main()
{
int t;
int n;
int cas = 0;
int b[147];
scanf("%d",&t);
while(t--)
{
int k = 0;
scanf("%d",&n);
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
}
int p = 0;
for(int i = n; i >= 1; i--)//先放最大的
{
if(a[i] == i)
continue;//已经放好了,既然等于i那么一定是向上的
for(int j = 1; j <= n; j++)
{
if(fabs(a[j]) == i)//找到应该放下面的那块煎饼的位置
{
p = j;
}
}
if(p != 1)//把当前要放到下面的先放到最上面,如果本来就在最上面这步就不需要了
{
reserve(p);
b[k++] = p;
}
if(a[1] > 0)//如果最上面是向上,则翻为向下,因为下面还要再翻一次
{
a[1] = -a[1];
b[k++] = 1;
}
if(i != 1)//把最上面的放到下面
{
b[k++] = i;
reserve(i);
}
else
{
b[k++] = 1;
a[1] = -a[1];
}
}
printf("%d %d",++cas,k);
for(int i = 0; i < k; i++)
{
printf(" %d",b[i]);
}
printf("\n");
}
return 0;
}