数据结构-A*算法2
这篇文章还可以在这里找到 英语
这篇blog是由iOS Tutorial Team的成员 Johann Fradj发表的,他目前是一位全职的资深iOS开发工程师。他是Hot Apps Factory的创始人,该公司开发了App Cooker。
你是否在做一款游戏的时候想创造一些怪兽或者游戏主角,让它们移动到特定的位置,避开墙壁和障碍物呢?
如果是的话,请看这篇教程,我们会展示如何使用A星寻路算法来实现它!
在网上已经有很多篇关于A星寻路算法的文章,但是大部分都是提供给已经了解基本原理的高级开发者的。
本篇教程将从最基本的原理讲起。我们会一步步讲解A星寻路算法,幷配有很多图解和例子。
不管你使用的是什么编程语言或者操作平台,你会发现本篇教程很有帮助,因为它在非编程语言的层面上解释了算法的原理。稍后,会有一篇教程,展示如何在Cocos2D iPhone 游戏中实现A星算法。
现在找下到达一杯咖啡因饮料和美味的零食的最短路径,开始吧!:]
一只探路猫
让我们想象一下,有一款游戏,游戏中一只猫想要找到获取骨头的路线。
“为什么会有一只猫想要骨头?!”你可能会这么想。在本游戏中, 这是一只狡猾的猫,他想捡起骨头给狗,以防止被咬死!:]
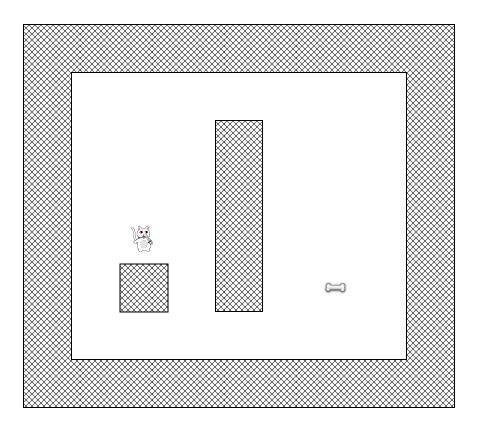
现在想像一下下图中的猫想找到到达骨头的最短路径:
不幸的是,猫不能直接从它当前的位置走到骨头的位置,因为有面墙挡住了去路,而且它在游戏中不是一只幽灵猫!
游戏中的猫同样懒惰,它总是想找到最短路径,这样当他回家看望它的女朋友时不会太累:-)
但是我们如何编写一个算法计算出猫要选择的那条路径呢?A星算法拯救了我们!
简化搜索区域
寻路的第一步是简化成容易控制的搜索区域。
怎么处理要根据游戏来决定了。例如,我们可以将搜索区域划分成像素点,但是这样的划分粒度对于我们这款基于方块的游戏来说太高了(没必要)。
作为代替,我们使用方块(一个正方形)作为寻路算法的单元。其他的形状类型也是可能的(比如三角形或者六边形),但是正方形是最简单并且最适合我们需求的。
像那样去划分,我们的搜索区域可以简单的用一个地图大小的二维数组去表示。所以如果是25*25方块大小的地图,我们的搜索区域将会是一个有625个正方形的数组。如果我们把地图划分成像素点,搜索区域就是一个有640,000个正方形的数组了(一个方块是32*32像素)!
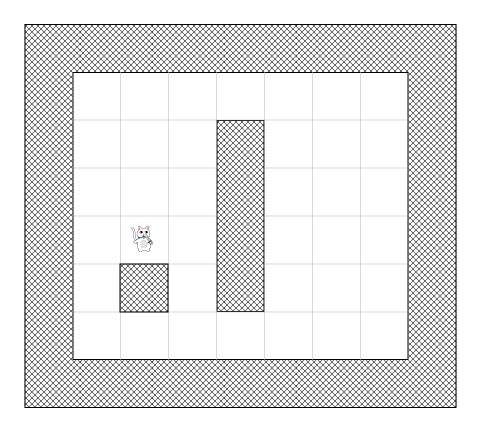
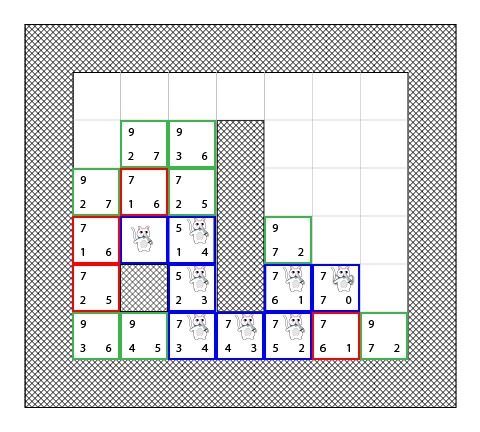
现在让我们基于目前的区域,把区域划分成多个方块来代表搜索空间(在这个简单的例子中,7*6个方块 = 42 个方块):
Open和Closed列表
既然我们创建了一个简单的搜索区域,我们来讨论下A星算法的工作原理吧。
除了懒惰之外,我们的猫没有好的记忆力,所以它需要两个列表:
- 一个记录下所有被考虑来寻找最短路径的方块(称为open 列表)
- 一个记录下不会再被考虑的方块(成为closed列表)
猫首先在closed列表中添加当前位置(我们把这个开始点称为点 “A”)。然后,把所有与它当前位置相邻的可通行小方块添加到open列表中。
现在猫需要判断在这些选项中,哪项才是最短路径,但是它要如何去选择呢?
在A星寻路算法中,通过给每一个方块一个和值,该值被称为路径增量。让我们看下它的工作原理!
路径增量
我们将会给每个方块一个G+H 和值:
- G是从开始点A到当前方块的移动量。所以从开始点A到相邻小方块的移动量为1,该值会随着离开始点越来越远而增大。
- H是从当前方块到目标点(我们把它称为点B,代表骨头!)的移动量估算值。这个常被称为探视,因为我们不确定移动量是多少 – 仅仅是一个估算值。
你也许会对“移动量”感兴趣。在游戏中,这个概念很简单 – 仅仅是方块的数量。
然而,在游戏中你可以对这个值做调整。例如:
- 如果你允许对角线移动,你可以针对对角线移动把移动量调得大一点。
- 如果你有不同的地形,你可以将相应的移动量调整得大一点 – 例如针对一块沼泽,水,或者猫女海报:-)
这就是大概的意思 – 现在让我们详细分析下如何计算出G和H值。
关于G值
G是从开始点A到达当前方块的移动量(在本游戏中是指方块的数目)。
为了计算出G的值,我们需要从它的前继(上一个方块)获取,然后加1。所以,每个方块的G值代表了从点A到该方块所形成路径的总移动量。
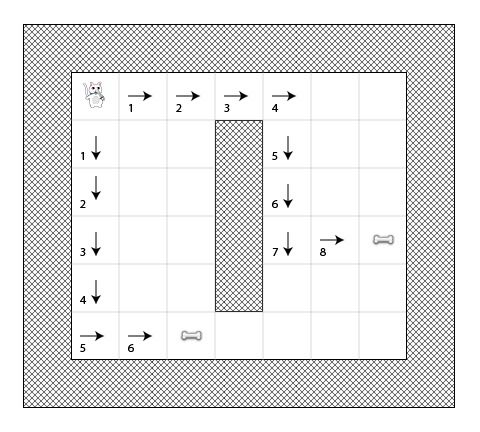
例如,下图展示了两条到达不同骨头的路径,每个方块都标有它的G值:
关于H值
H值是从当前方块到终点的移动量估算值(在本游戏中是指方块的数目)。
移动量估算值离真实值越接近,最终的路径会更加精确。如果估算值停止作用,很可能生成出来的路径不会是最短的(但是它可能是接近的)。这个题目相对复杂,所以我们不会再本教程中讲解,但是我在教程的末尾提供了一个网络链接,对它做了很好的解释。
为了让它更简单,我们将使用“曼哈顿距离方法”(也叫“曼哈顿长”或者“城市街区距离”),它只是计算出距离点B,剩下的水平和垂直的方块数量,略去了障碍物或者不同陆地类型的数量。
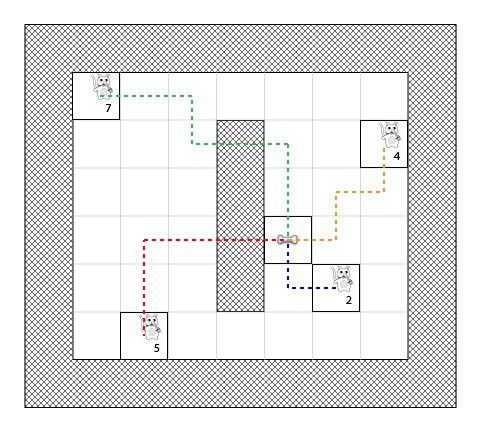
例如,下图展示了使用“城市街区距离”,从不同的开始点到终点,去估算H的值(黑色字):
A星算法
既然你知道如何计算每个方块的和值(我们将它称为F,等于G+H), 我们来看下A星算法的原理。
猫会重复以下步骤来找到最短路径:
- 将方块添加到open列表中,该列表有最小的和值。且将这个方块称为S吧。
- 将S从open列表移除,然后添加S到closed列表中。
- 对于与S相邻的每一块可通行的方块T:
- 如果T在closed列表中:不管它。
- 如果T不在open列表中:添加它然后计算出它的和值。
- 如果T已经在open列表中:当我们使用当前生成的路径到达那里时,检查F 和值是否更小。如果是,更新它的和值和它的前继。
如果你对它的工作原理还有点疑惑,不用担心 – 我们会用例子一步步介绍它的原理!:]
猫的路径
让我们看下我们的懒猫到达骨头的行程例子。
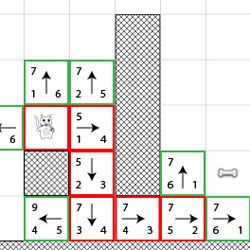
在下图中,我根据以下内容,列出了公式F = G + H 中的每项值:
- F(方块的和值):左上角
- G(从A点到方块的移动量):左下角
- H(从方块到B点的估算移动量): 右下角
同时,箭头指示了到达相应方块的移动方向。
最后,在每一步中,红色方块表示closed列表,绿色方块表示open列表。
好的,我们开始吧!
第一步
第一步,猫会确定相对于开始位置(点A)的相邻方块,计算出他们的F和值,然后把他们添加到open列表中:

你会看到每个方块都列出了H值(有两个是6,一个是4)。我建议根据“城市街区距离”去计算方块的相关值,确保你理解了它的原理。
同时注意F值(在左上角)是G(左下角)值和H(右下脚)值的和。
第二步
在第二步中,猫选择了F和值最小的方块,把它添加到closed列表中,然后检索它的相邻方块的相关数值。
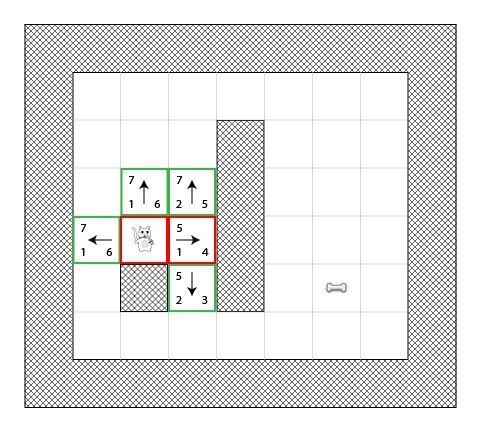
现在你将看到拥有最小增量的是F值为4的方块。猫尝试添加所有相邻的方块到open列表中(然后计算他们的和值),除了猫自身的方块不能添加以外(因为它已经被添加到了closed列表中)或者它是墙壁方块(因为它不能通行)。
注意被添加到open列表的两个新方块,他们的G值都增加了1,因为他们现在离开始点有2个方块远了。你也许需要再计算下“城市街区距离”以确保你理解了每个新方块的H值。
第三步
再次,我们选择了有最小F和值(5)的方块,继续重复之前的步骤:

现在,只有一个可能的方块被添加到open列表中了,因为已经有一个相邻的方块在close列表中,其他两个是墙壁方块。
第四步
现在我们遇到了一个有趣的情况。正如你之前看到的,有4个方块的F和值都为7 – 我们要怎么做呢?!
有几种解决方法可以使用,但是最简单(快速)的方法是一直跟着最近被添加到open列表中的方块。现在继续沿着最近被添加的方块前进。

这次有两个可通过的相邻方块了,我们还是像之前那样计算他们的和值。
第五步
我们越来越接近终点了!
第六步
我们差不多到终点了,但是这次你看到有两条到达骨头的最短路径提供给我们选择:

在我们的例子中,有两条最短路径:
- 1-2-3-4-5-6
- 1-2-3-4-5-7
It doesn’t really matter which of these we choose, it comes down to the actual implementation in code.
选择哪一条其实没关系,现在到了真正用代码实现的时候了。
第七步
啊哈,骨头在open列表中了!
第八步
现在目标方块在open列表中了,算法会把它添加到closed列表中:

一只有远见的猫
在上面的例子中,我们看到当猫在寻找最短路径时,它经常选择更好的方块(那个在它的未来最短路径上的方块)- 好像它是一只有远见的猫!
但是如果猫是盲目的,并且总是选择第一个添加到它的列表上的方块,会发生什么事情?
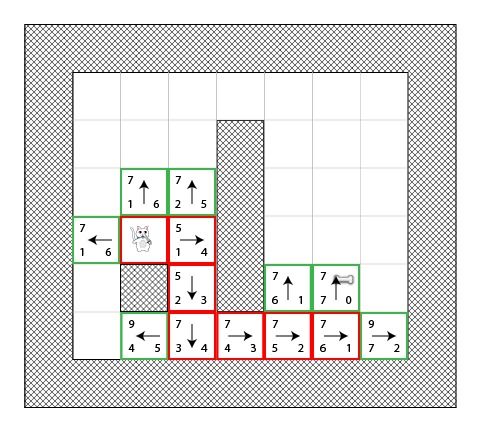
下图展示了所有在寻找过程中会被使用到的方块。你会看到猫在尝试更多的方块,但是它仍然找到了最短路径(不是之前的那条,而是另一条等价的):
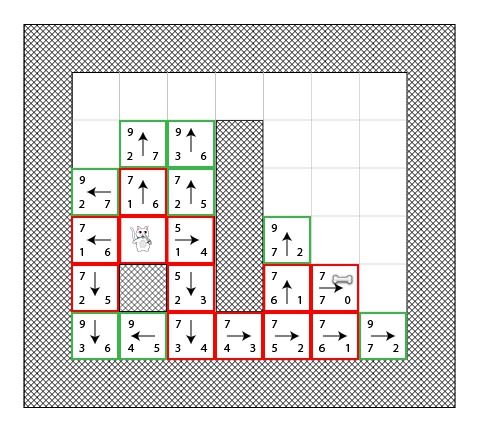
图中的红色方块不代表最短路径,它们只是代表在某个时候被选择为“S”的方块。
我建议你看着上面的图,并且尝试过一遍步骤。这次无论你看到哪个相邻的方块,都选择“最坏”的方式去走。你会发现最后还是找到了最短路径!
所以你可以看到跟随一个“错误的”方块是没有问题的,你仍然会在多次重复尝试后找到最短路径。
所以在我们的实现中,我们会按照以下的算法添加方块到open列表中:
- 相邻的方块会返回这些顺序: 上面/左边/下面/右边。
- 当所有的方块都有相同的和值后,方块会被添加到open列表中(所以第一个被添加的方块是第一个被猫挑选的)。
//我收藏的一个很不错的A*算法
/*
;===================================================================
;A* Pathfinder - Do Not Use
;===================================================================
;Last updated 06/16/03 -- Visual C++ version
;This version of the A* Library has been written specifically for the
;Astar Demo 1 program. If you want to use the AStar functions in your
;program, use the Demo 2 A* library. The primary difference between
;them is that this one accomodates stepByStep searches, which are
;specific to Demo 1. The code included to handle that will
;probably malfunction if used in another program -- so use the other
;version (see Demo 2) instead.
;==================================================================
*/
const mapWidth = 16, mapHeight = 12, tileSize = 50, numberPeople = 1;
int onClosedList = 10;
const notfinished = 0, notStarted = 0;// path-related constants
const found = 1, nonexistent = 2;
const walkable = 0, unwalkable = 1;// walkability array constants
//Create needed arrays
char walkability [mapWidth][mapHeight];
int openList[mapWidth*mapHeight+2]; //1 dimensional array holding ID# of open list items
int whichList[mapWidth+1][mapHeight+1]; //2 dimensional array used to record
// whether a cell is on the open list or on the closed list.
int openX[mapWidth*mapHeight+2]; //1d array stores the x location of an item on the open list
int openY[mapWidth*mapHeight+2]; //1d array stores the y location of an item on the open list
int parentX[mapWidth+1][mapHeight+1]; //2d array to store parent of each cell (x)
int parentY[mapWidth+1][mapHeight+1]; //2d array to store parent of each cell (y)
int Fcost[mapWidth*mapHeight+2]; //1d array to store F cost of a cell on the open list
int Gcost[mapWidth+1][mapHeight+1]; //2d array to store G cost for each cell.
int Hcost[mapWidth*mapHeight+2]; //1d array to store H cost of a cell on the open list
int pathLength[numberPeople+1]; //stores length of the found path for critter
int pathLocation[numberPeople+1]; //stores current position along the chosen path for critter
int* pathBank [numberPeople+1];
//Path reading variables
int pathStatus[numberPeople+1];
int xPath[numberPeople+1];
int yPath[numberPeople+1];
//-----------------------------------------------------------------------------
// Function Prototypes: where needed
//-----------------------------------------------------------------------------
void ReadPath(int pathfinderID,int currentX,int currentY, int pixelsPerFrame);
int ReadPathX(int pathfinderID,int pathLocation);
int ReadPathY(int pathfinderID,int pathLocation);
void RenderScreen (bool stepByStep=false);
//-----------------------------------------------------------------------------
// Name: InitializePathfinder
// Desc: Allocates memory for the pathfinder.
//-----------------------------------------------------------------------------
void InitializePathfinder (void)
{
for (int x = 0; x < numberPeople+1; x++)
pathBank [x] = (int*) malloc(4);
}
//-----------------------------------------------------------------------------
// Name: EndPathfinder
// Desc: Frees memory used by the pathfinder.
//-----------------------------------------------------------------------------
void EndPathfinder (void)
{
for (int x = 0; x < numberPeople+1; x++)
{
free (pathBank [x]);
}
}
//-----------------------------------------------------------------------------
// Name: FindPath
// Desc: Finds a path using A*
//-----------------------------------------------------------------------------
int FindPath (int pathfinderID,int startingX, int startingY,
int targetX, int targetY, bool stepByStep = false)
{
int onOpenList=0, parentXval=0, parentYval=0,
a=0, b=0, m=0, u=0, v=0, temp=0, corner=0, numberOfOpenListItems=0,
addedGCost=0, tempGcost = 0, path = 0, x=0, y=0,
tempx, pathX, pathY, cellPosition,
newOpenListItemID=0;
//1. Convert location data (in pixels) to coordinates in the walkability array.
int startX = startingX/tileSize;
int startY = startingY/tileSize;
targetX = targetX/tileSize;
targetY = targetY/tileSize;
//2.Quick Path Checks: Under the some circumstances no path needs to
// be generated ...
// If starting location and target are in the same location...
if (startX == targetX && startY == targetY && pathLocation[pathfinderID] > 0)
return found;
if (startX == targetX && startY == targetY && pathLocation[pathfinderID] == 0)
return nonexistent;
// If target square is unwalkable, return that it's a nonexistent path.
if (walkability[targetX][targetY] == unwalkable)
goto noPath;
//3.Reset some variables that need to be cleared
for (x = 0; x < mapWidth; x++)
{
for (y = 0; y < mapHeight;y++)
whichList [x][y] = 0;
}
onClosedList = 2; //changing the values of onOpenList and onClosed list is faster than redimming whichList() array
onOpenList = 1;
pathLength [pathfinderID] = notStarted;//i.e, = 0
pathLocation [pathfinderID] = notStarted;//i.e, = 0
Gcost[startX][startY] = 0; //reset starting square's G value to 0
//4.Add the starting location to the open list of squares to be checked.
numberOfOpenListItems = 1;
openList[1] = 1;//assign it as the top (and currently only) item in the open list, which is maintained as a binary heap (explained below)
openX[1] = startX ; openY[1] = startY;
//5.Do the following until a path is found or deemed nonexistent.
do
{
//6.If the open list is not empty, take the first cell off of the list.
// This is the lowest F cost cell on the open list.
if (numberOfOpenListItems != 0)
{
//7. Pop the first item off the open list.
parentXval = openX[openList[1]];
parentYval = openY[openList[1]]; //record cell coordinates of the item
whichList[parentXval][parentYval] = onClosedList;//add the item to the closed list
// Open List = Binary Heap: Delete this item from the open list, which
// is maintained as a binary heap. For more information on binary heaps, see:
// http://www.policyalmanac.org/games/binaryHeaps.htm
numberOfOpenListItems = numberOfOpenListItems - 1;//reduce number of open list items by 1
// Delete the top item in binary heap and reorder the heap, with the lowest F cost item rising to the top.
openList[1] = openList[numberOfOpenListItems+1];//move the last item in the heap up to slot #1
v = 1;
// Repeat the following until the new item in slot #1 sinks to its proper spot in the heap.
do
{
u = v;
if (2*u+1 <= numberOfOpenListItems) //if both children exist
{
//Check if the F cost of the parent is greater than each child.
//Select the lowest of the two children.
if (Fcost[openList[u]] >= Fcost[openList[2*u]])
v = 2*u;
if (Fcost[openList[v]] >= Fcost[openList[2*u+1]])
v = 2*u+1;
}
else
{
if (2*u <= numberOfOpenListItems) //if only child #1 exists
{
//Check if the F cost of the parent is greater than child #1
if (Fcost[openList[u]] >= Fcost[openList[2*u]])
v = 2*u;
}
}
if (u != v) //if parent's F is > one of its children, swap them
{
temp = openList[u];
openList[u] = openList[v];
openList[v] = temp;
}
else
break; //otherwise, exit loop
}
while (!KeyDown(27));//reorder the binary heap
[code=C/C++]//7.Check the adjacent squares. (Its "children" -- these path children // are similar, conceptually, to the binary heap children mentioned // above, but don't confuse them. They are different. Path children // are portrayed in Demo 1 with grey pointers pointing toward // their parents.) Add these adjacent child squares to the open list // for later consideration if appropriate (see various if statements // below). for (b = parentYval-1; b <= parentYval+1; b++){ for (a = parentXval-1; a <= parentXval+1; a++){ // If not off the map (do this first to avoid array out-of-bounds errors) if (a != -1 && b != -1 && a != mapWidth && b != mapHeight){ // If not already on the closed list (items on the closed list have // already been considered and can now be ignored). if (whichList[a][b] != onClosedList) { // If not a wall/obstacle square. if (walkability [a][b] != unwalkable) { // Don't cut across corners corner = walkable; if (a == parentXval-1) { if (b == parentYval-1) { if (walkability[parentXval-1][parentYval] == unwalkable || walkability[parentXval][parentYval-1] == unwalkable) \ corner = unwalkable; } else if (b == parentYval+1) { if (walkability[parentXval][parentYval+1] == unwalkable || walkability[parentXval-1][parentYval] == unwalkable) corner = unwalkable; } } else if (a == parentXval+1) { if (b == parentYval-1) { if (walkability[parentXval][parentYval-1] == unwalkable || walkability[parentXval+1][parentYval] == unwalkable) corner = unwalkable; } else if (b == parentYval+1) { if (walkability[parentXval+1][parentYval] == unwalkable || walkability[parentXval][parentYval+1] == unwalkable) corner = unwalkable; } } if (corner == walkable) { // If not already on the open list, add it to the open list. if (whichList[a][b] != onOpenList) { //Create a new open list item in the binary heap. newOpenListItemID = newOpenListItemID + 1; //each new item has a unique ID # m = numberOfOpenListItems+1; openList[m] = newOpenListItemID;//place the new open list item (actually, its ID#) at the bottom of the heap openX[newOpenListItemID] = a; openY[newOpenListItemID] = b;//record the x and y coordinates of the new item //Figure out its G cost if (abs(a-parentXval) == 1 && abs(b-parentYval) == 1) addedGCost = 14;//cost of going to diagonal squares else addedGCost = 10;//cost of going to non-diagonal squares Gcost[a][b] = Gcost[parentXval][parentYval] + addedGCost; //Figure out its H and F costs and parent Hcost[openList[m]] = 10*(abs(a - targetX) + abs(b - targetY)); Fcost[openList[m]] = Gcost[a][b] + Hcost[openList[m]]; parentX[a][b] = parentXval ; parentY[a][b] = parentYval; //Move the new open list item to the proper place in the binary heap. //Starting at the bottom, successively compare to parent items, //swapping as needed until the item finds its place in the heap //or bubbles all the way to the top (if it has the lowest F cost). while (m != 1) //While item hasn't bubbled to the top (m=1) { //Check if child's F cost is < parent's F cost. If so, swap them. if (Fcost[openList[m]] <= Fcost[openList[m/2]]) { temp = openList[m/2]; openList[m/2] = openList[m]; openList[m] = temp; m = m/2; } else break; } numberOfOpenListItems = numberOfOpenListItems+1;//add one to the number of items in the heap //Change whichList to show that the new item is on the open list. whichList[a][b] = onOpenList; } //8.If adjacent cell is already on the open list, check to see if this // path to that cell from the starting location is a better one. // If so, change the parent of the cell and its G and F costs. else //If whichList(a,b) = onOpenList { //Figure out the G cost of this possible new path if (abs(a-parentXval) == 1 && abs(b-parentYval) == 1) addedGCost = 14;//cost of going to diagonal tiles else addedGCost = 10;//cost of going to non-diagonal tiles tempGcost = Gcost[parentXval][parentYval] + addedGCost; //If this path is shorter (G cost is lower) then change //the parent cell, G cost and F cost. if (tempGcost < Gcost[a][b]) //if G cost is less, { parentX[a][b] = parentXval; //change the square's parent parentY[a][b] = parentYval; Gcost[a][b] = tempGcost;//change the G cost //Because changing the G cost also changes the F cost, if //the item is on the open list we need to change the item's //recorded F cost and its position on the open list to make //sure that we maintain a properly ordered open list. for (int x = 1; x <= numberOfOpenListItems; x++) //look for the item in the heap { if (openX[openList[x]] == a && openY[openList[x]] == b) //item found { Fcost[openList[x]] = Gcost[a][b] + Hcost[openList[x]];//change the F cost //See if changing the F score bubbles the item up from it's current location in the heap m = x; while (m != 1) //While item hasn't bubbled to the top (m=1) { //Check if child is < parent. If so, swap them. if (Fcost[openList[m]] < Fcost[openList[m/2]]) { temp = openList[m/2]; openList[m/2] = openList[m]; openList[m] = temp; m = m/2; } else break; } break; //exit for x = loop } //If openX(openList(x)) = a } //For x = 1 To numberOfOpenListItems }//If tempGcost < Gcost(a,b) }//else If whichList(a,b) = onOpenList }//If not cutting a corner }//If not a wall/obstacle square. }//If not already on the closed list }//If not off the map }//for (a = parentXval-1; a <= parentXval+1; a++){ }//for (b = parentYval-1; b <= parentYval+1; b++){ }//if (numberOfOpenListItems != 0) //9.If open list is empty then there is no path. else { path = nonexistent; break; } //If target is added to open list then path has been found. if (whichList[targetX][targetY] == onOpenList) { path = found; break; } //If in step-by-step mode draw the screen step by step, waiting //for a keypress before the next step is taken. if (path == notfinished && stepByStep == true) { RenderScreen(stepByStep); while (1) //while "1" or "enter" or "escape" key not hit { if (KeyHit(13) || KeyDown(27)) //if enter or escape hit { stepByStep = false; break; } if (KeyHit(49)) break; //if "1" key hit CheckWinMessages(); } } } while (!(KeyDown(27)));//Do until path is found or deemed nonexistent //10.Save the path if it exists. if (path == found) { //a.Working backwards from the target to the starting location by checking // each cell's parent, figure out the length of the path. pathX = targetX; pathY = targetY; do { //Look up the parent of the current cell. tempx = parentX[pathX][pathY]; pathY = parentY[pathX][pathY]; pathX = tempx; //Figure out the path length pathLength[pathfinderID] = pathLength[pathfinderID] + 1; } while (pathX != startX || pathY != startY); //b.Resize the data bank to the right size in bytes pathBank[pathfinderID] = (int*) realloc (pathBank[pathfinderID], pathLength[pathfinderID]*8); //c. Now copy the path information over to the databank. Since we are // working backwards from the target to the start location, we copy // the information to the data bank in reverse order. The result is // a properly ordered set of path data, from the first step to the // last. pathX = targetX ; pathY = targetY; cellPosition = pathLength[pathfinderID]*2;//start at the end do { cellPosition = cellPosition - 2;//work backwards 2 integers pathBank[pathfinderID] [cellPosition] = pathX; pathBank[pathfinderID] [cellPosition+1] = pathY; //d.Look up the parent of the current cell. tempx = parentX[pathX][pathY]; pathY = parentY[pathX][pathY]; pathX = tempx; //e.If we have reached the starting square, exit the loop. } while (pathX != startX || pathY != startY); } return path; //13.If there is no path to the selected target, set the pathfinder's // xPath and yPath equal to its current location and return that the // path is nonexistent. noPath: xPath[pathfinderID] = startingX; yPath[pathfinderID] = startingY; return nonexistent; } //----------------------------------------------------------------------------- // Name: ReadPath // Desc: Reads path data created by FindPath() //----------------------------------------------------------------------------- void ReadPath(int pathfinderID) //If a path exists, read the path data // from the pathbank. { pathLocation[pathfinderID] = 1; //set pathLocation to 1st step while (pathLocation[pathfinderID] < pathLength[pathfinderID]) { int a = pathBank[pathfinderID] [pathLocation[pathfinderID]*2-2]; int b = pathBank[pathfinderID] [pathLocation[pathfinderID]*2-1]; pathLocation[pathfinderID] = pathLocation[pathfinderID] + 1; whichList[a][b] = 3;//draw dotted path } }