hdu 4717 - The Moving Points(三分)
本解析转自:http://www.cnblogs.com/acmdeweilai/archive/2013/09/11/3315769.html
说明下为啥满足三分:
设y=f(x) (x>0)表示任意两个点的距离随时间x的增长,距离y的变化。则f(x)函数单调性有两种:1.先单减,后单增。2.一直单增。
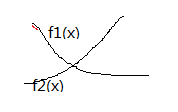
设y=m(x) (x>0)表示随时间x的增长,所有点的最大距离y的变化。即m(x)是所有点对构成的f(x)图像取最上面的部分。则m(x)的单调性也只有两种可能:1.先单减,后单增。2.一直单增。 这个地方的证明可以这样:假如时刻t1到时刻t2最大值取得是函数f1(x)的图像,在时刻t2到时刻t3取得是f2(x)的图像,
那么由图可以看出f2(x)的斜率大于f1(x)的斜率(会有折点)
可以归纳出m(x)函数的斜率是递增。那么单调性就可以知道了。
m(x)有了上面的性质,就可以有三分了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
#include <set>
#include <map>
#define M 305
#define mod 1000000007
#define INF 0x7fffffff
#define eps 1e-6
#define LL long long
#define LLU unsigned long long
using namespace std;
struct Point{
int x, y, dx, dy;
int readPoint()
{
return scanf("%d%d%d%d", &x, &y, &dx, &dy);
}
}st[M];
int dcmp(double x)
{
if(x<eps) return 0;
return x<0?-1:1;
}
double dis(Point a, Point b, double time)
{
double x = (a.x+time*a.dx)-(b.x+time*b.dx);
double y = (a.y+time*a.dy)-(b.y+time*b.dy);
return sqrt(x*x+y*y);
}
int n;
double val(double x)
{
double ans = 0.0;
for(int i = 0; i < n; ++i)
for(int j = i+1; j < n; ++j)
ans = max(ans, dis(st[i], st[j], x));
return ans;
}
int main ()
{
int t, k = 0;
scanf("%d",&t);
while(t--)
{
scanf("%d", &n);
for(int i = 0; i < n; ++i)
st[i].readPoint();
double l = 0.0, r = 100.0;
while(dcmp(r-l)>0)
{
double mid = (l+r)/2;
double midmid = (mid+r)/2;
if(dcmp(val(mid)-val(midmid))>0)
l = mid;
else
r = midmid;
}
printf("Case #%d: %.2lf %.2lf\n", ++k, l, val(l));
}
return 0;
}