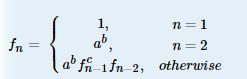HDU 5667 Sequence(矩阵快速幂+费马小定理)

大意：

He gives you 5 numbers n,a,b,c,p,and he will eat fn foods.But there are only p foods,so you should tell him fn mod p.

Input
The first line has a number,T,means testcase.

Each testcase has 5 numbers,including n,a,b,c,p in a line.

1≤T≤10,1≤n≤1018,1≤a,b,c≤109,p is a prime number,and p≤109+7.

思路：矩阵快速幂一定可以，那么a的指数很大怎么处理呢那么用费马小定理a^(p-1)%p=1;a^(m%(p-1)) %p=1 ; 最后注意 a%p==0的情况。

//|G(n) | |c 1 b| |G(n-1)| 
//|G(n-1)|= |1 0 0|* |G(n-2)| 
//|1 | |0 0 1| |1 | 
#include<map>
#include<queue>
#include<cmath>
#include<cstdio>
#include<stack>
#include<iostream>
#include<cstring>
#include<algorithm>
#define LL int
#define inf 0x3f3f3f3f
#define eps 1e-8
#include<vector>
#define ls l,mid,rt<<1
#define rs mid+1,r,rt<<1|1

using namespace std;
__int64 mod ,p;

struct node{
    __int64 r[15][15];
}q;

void matrix_pow(node &a,node &b){
    int i,j,k;
    node t;
    for(i= 0;i <3;++ i){
        for(j = 0;j < 3;++ j){
            t.r[i][j]  = 0;
        }
    }
    for(k = 0;k < 3;++ k){
        for(i =0 ;i < 3;i++){
            for(j = 0;j < 3;++ j){
                t.r[i][j] = (t.r[i][j]+a.r[i][k]*b.r[k][j])%mod;
            }
        }
    }
    a = t;
}

void so(node &q,__int64 m){

    __int64 i,j,k;
    node tmp;
    for(i= 0;i <3;++ i){
        for(j = 0;j < 3;++ j){
            tmp.r[i][j]  = 0;
        }
    }
    for(i=0;i<3;++i)
        tmp.r[i][i]=1;

    while(m){
        if(m&1){
           matrix_pow(tmp,q);
        }
        matrix_pow(q,q);
        m =m >> 1;
    }
   q = tmp;
}
__int64 qick(__int64 x,__int64 y){
    x = x%p;
    __int64 ba  = x,r = 1;
    while(y){
        if(y&1)
            r = (r*ba) % p;
        ba  = (ba * ba) % p;
        y >>= 1;
    }
    return r;
}
int main(){
    __int64 k,i,j,n,a,b,c;
    int cla;
    scanf("%d",&cla);
    while(cla--){
        scanf("%I64d %I64d %I64d %I64d %I64d",&n,&a,&b,&c,&p);

        if(n == 1){
            printf("1\n");continue;
        }
        else if(n==2){
            printf("%I64d\n",qick(a,b));continue;
        }

        else if(a%p==0){
            puts("0");continue;
        }

        mod = p - 1;
        memset(q.r,0,sizeof(q.r));
        q.r[0][0] = c,q.r[0][2]=b;
        q.r[0][1] = q.r[1][0] = q.r[2][2] = 1;
        so(q,n-2);

        __int64 ans  =0;

        ans = (ans + b*q.r[0][0])%mod;
        ans = (ans + q.r[0][2])%mod;

        printf("%I64d\n",qick(a,ans));
    }
    return 0;
}