DirectX学习之-------从零做起
由于工作的缘故,我从运动控制领域转行到三维图形开发方面,实在是有些讽刺。不过,本人有些不太服气,别人可以学好的,我一样可以。如今要学习DirectX,可以说我还尚未入门,希望各位大虾们切莫笑话。学习DirectX的技术,当然要从基本的计算机图形学基础知识学起。
坐标参照系
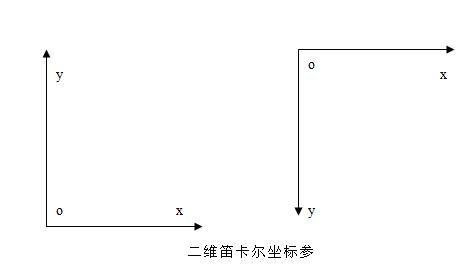
1、二维笛卡尔坐标参照系
二维笛卡尔参照坐标系有两种可能形式:一种是Y轴向上,另一种是Y轴向下。也即坐标原点前一种位于左下角,后者位于左上角。在计算机中,有的将坐标远点置于屏幕左上角,有的置于屏幕中心。
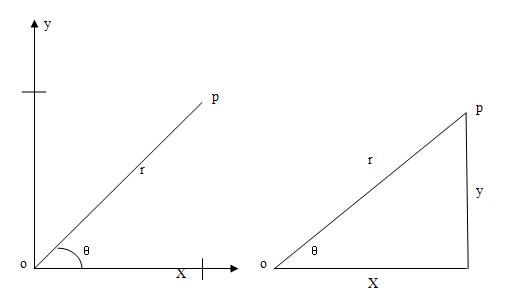
2、XY平面的极坐标系
常用的非笛卡尔坐标系就是极坐标系。其中,坐标位置由坐标到原点的极径距离r和距水平轴的角位移量θ指定。正角的位移量是逆时针的,负的角位移量是顺时针的。从笛卡尔坐标系到极坐标系的变换公式为:
角度可由指定度数或弧度给出。θ角的弧度值计算如下:θ=s/r.
此外还有三维笛卡尔坐标系,这里就需要注意使用的时候是左手坐标系还是右手坐标系。比较常用的就是笛卡尔直角坐标系了,也叫正交坐标系。
2、 点和向量
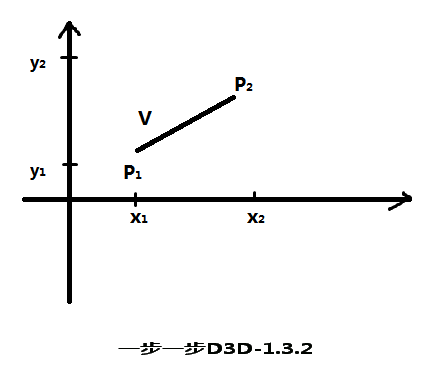
点和向量的概念有根本的区别。点是某参照系以坐标值指定的位置,一个向量(矢量)定义为两个点位置之间的差。它有大小,有方向。对于二维向量来说:
V=P2-P1
=(x2-x1,y2-y1)
=(Vx,Vy)
Vx,Vy分别是V在X轴和Y轴上的投影,给定两点位置可得任何坐标系下的向量分量。
所以二维向量V的大小便是:
___________ ________________
|V|=√ Vx2+Vy2 =√(x2-x1)2+(y2-y1)2
它的方向可以根据离x轴的角位移量给出:
α=tan-1(Vy/Vx)
而如果是三维空间向量大小则为:
_______________
|V|=√ Vx2+Vy2+Vz2
V,即是向量的长度也叫做向量的模。
此中向量的方向由方向角α、β、γ给出,其实就是求该向量与各个坐标轴形成的角:
cosα=Vx / |V|` cosβ=Vy / |V|` cosγ=Vz / |V|
cosα、cosβ、cosγ为向量的方向余弦。实际上为指定V的方向,只需两个方向余弦。因为:
cos2α+cos2β+cos2γ=1
2.1 向量相加与定比例相乘
V1+V2=(V1x+V2x, V1y+V2y, V1z+V2z)
向量与标量相加无意义。因为标量是一个数值,向量可能有多个数值分量。
向量与标量的乘法(数乘):aV=(aVx,aVy,aVz)
2.2 两个向量的标量积
产生标量的向量乘法:V1*V2=|V1||V2|cosθ 0≤θ≤π
在笛卡尔坐标系中标量积(点乘)的计算: V1*V2= V1x*V2x + V1y*V2y + V1z*V2z
而点积是可以交换的:V1*V2 = V2*V1
点积(点乘)的关于向量是遵循加法分配律的:V1*(V2+V3)=V1*V2 + V1*V3
由标量积,我们可知:
两向量相乘:
结果等于0,则两向量互相垂直;
结果大于0,则两向量之间的夹角小于90度;
结果小于0,则两向量之间的夹角大于90度。
2.3 两向量的向量积 (叉积)
能产生一个向量的两个向量的乘法:V1 ×(注:叉乘) V2=u|V1||V2|sinθ 0≤θ≤π
u是垂直与V1 、 V2 的单位向量(1),而u的方向则取决于使用的坐标系是左手还是右手,拇指方向即为u的方向。这个积叫做两个向量的叉积(向量积)。它是垂直与两个向量所在平面的向量,他的大小等于这两个向量与坐标轴形成的平行四边形的面积。
当然,也可以借助指定坐标系的向量分量来表达叉积。笛卡尔坐标系中:
叉积的分量=V1 ×(叉乘) V2=(V1y*V2x - V1z*V2y , V1z*V2x - V1x*V2z , V1x*V2y - V1y*V2x)
如果令ux、uy、uz 表示沿x, y ,z 轴的单位向量, 那借助笛卡尔分量以行列格式写出叉积,则:
| ux uy uz |
V1 X V2 = | V1x V1y V1z |
| V2x V2y V2z |
任意两个平行向量的叉积是0。这里需要注意叉积并不满足交换律,而是满足反交换律 :V1 X V2 = -(V2 X V1)
此外,叉积并不满足结合律 V1 X (V2 X V3)≠(V1 X V2) X V3
不过叉积关于向量的加法还是可以分配的:V1 X (V2 + V3)≠(V1 X V2) +(V1 X V3)
在D3D中,点与向量关系密切。在D3D库中,表示向量的数据结构有:
D3DXVECTOR2 ,D3DXVECTOR3,D3DXVECTOR4
1 typedef struct D3DXVECTOR3 : public D3DVECTOR
2 {
3 public:
4
5 D3DXVECTOR3() {};
6 D3DXVECTOR3( CONST FLOAT * );
7 D3DXVECTOR3( CONST D3DVECTOR& );
8 D3DXVECTOR3( CONST D3DXFLOAT16 * );
9 D3DXVECTOR3( FLOAT x, FLOAT y, FLOAT z );
10
11 // casting 类型转换
12 operator FLOAT* ();
13 operator CONST FLOAT* () const;
14
15 // assignment operators 分配运算符
16 D3DXVECTOR3& operator += ( CONST D3DXVECTOR3& );
17 D3DXVECTOR3& operator -= ( CONST D3DXVECTOR3& );
18 D3DXVECTOR3& operator *= ( FLOAT );
19 D3DXVECTOR3& operator /= ( FLOAT );
20
21 // unary operators 一元运算
22 D3DXVECTOR3 operator + () const;
23 D3DXVECTOR3 operator - () const;
24
25 // binary operators 二元运算
26 D3DXVECTOR3 operator + ( CONST D3DXVECTOR3& ) const;
27 D3DXVECTOR3 operator - ( CONST D3DXVECTOR3& ) const;
28 D3DXVECTOR3 operator * ( FLOAT ) const;
29 D3DXVECTOR3 operator / ( FLOAT ) const;
30 friend D3DXVECTOR3 operator * ( FLOAT, CONST struct D3DXVECTOR3& );
31 BOOL operator == ( CONST D3DXVECTOR3& ) const;
32 BOOL operator != ( CONST D3DXVECTOR3& ) const;
33
34 } D3DXVECTOR3, *LPD3DXVECTOR3;
35
36 //D3DXVECTOR3是从D3DVECTOR继承的
37
38 typedef struct _D3DVECTOR {
39 float x, y, z;
40 } D3DVECTOR;
41
42
1
6
7
8 // 计算向量大小:
9
10 FLOAT D3DXVec3Length( // Returns the magnitude.返回大小
11 CONST D3DXVECTOR3 * pV // The vector to compute the length of. 计算向量长度
12 );
13 D3DXVECTOR3 v( 1.0f , 2.0f , 3.0f );
14 float magnitude = D3DXVec3Length( & v ); // = sqrt(14)
15
16
17
18 // 规范(单位)化向量:
19
20 D3DXVECTOR3 * D3DXVec3Normalize(
21 D3DXVECTOR3 * pOut, // Result.
22 CONST D3DXVECTOR3 * pV // The vector to normalize.
23 );
24
25
26
27 // 向量加、减法:
28
29 D3DXVECTOR3 u( 2.0f , 0.0f , 1.0f );
30 D3DXVECTOR3 v( 0.0f , - 1.0f , 5.0f );
31 // (2.0 + 0.0, 0.0 + (-1.0), 1.0 + 5.0)
32 D3DXVECTOR3 sum = u + v; // = (2.0f, -1.0f, 6.0f)
33
34
35 D3DXVECTOR3 u( 2.0f , 0.0f , 1.0f );
36 D3DXVECTOR3 v( 0.0f , - 1.0f , 5.0f );
37 D3DXVECTOR3 difference = u - v; // = (2.0f, 1.0f, -4.0f)
38
39
40
41 // 数乘:
42
43 D3DXVECTOR3 u( 1.0f , 1.0f , - 1.0f );
44 D3DXVECTOR3 scaledVec = u * 10.0f ; // = (10.0f, 10.0f, -10.0f)
45
46
47
48 // 标量积(点积、点乘):
49
50 FLOAT D3DXVec3Dot( // Returns the result.
51 CONST D3DXVECTOR3 * pV1, // Left sided operand.
52 CONST D3DXVECTOR3 * pV2 // Right sided operand.
53 );
54 D3DXVECTOR3 u( 1.0f , - 1.0f , 0.0f );
55 D3DXVECTOR3 v( 3.0f , 2.0f , 1.0f );
56 // 1.0*3.0 + -1.0*2.0 + 0.0*1.0
57 // = 3.0 + -2.0
58 float dot = D3DXVec3Dot( & u, & v ); // = 1.0
59
60
61 // 叉乘:
62
63 D3DXVECTOR3 * D3DXVec3Cross(
64 D3DXVECTOR3 * pOut, // Result.
65 CONST D3DXVECTOR3 * pV1, // Left sided operand.
66 CONST D3DXVECTOR3 * pV2 // Right sided operand.
67 );
68
69
2.4 矩阵
若干个量组成的长方形队列就是矩阵。这些量自然就是矩阵的元素。这些量可以是数字、函数、数值表达式等,以行数和列数标识。行列相等的矩阵也叫方阵。如一个m*n的矩阵为:
{a11 a12 ... a1n }
A=| a21 a22 ... a2n |
{am1 am2 ... amn}
ajk的意思是矩阵A的j行,k列元素。也就是说任何元素的第一个下标代表行数,第二个为列数。 矩阵可以认为是行向量或列向量的集合,数学中往往以列矩阵表示向量:
{ Vx }
V=| Vy |
{ Vz }
2.4.1 标量乘法和矩阵加法
标量乘法:
若 矩阵A乘以标量S,则:S乘以A中的每一个元素从而得到相乘所得的矩阵。(S*ajx);
矩阵加法:
矩阵加法只有在两个矩阵行数和列数都相等才有意义,运算时各元素对应相加即可。矩阵加法满足分配律。
2.4.2 矩阵乘法
矩阵A的列数等于矩阵B的行数时:乘积矩阵C=A的行元素与B的列元素乘积的和 Ex:
{ 0 -1 } {0*1+(-1)*3 0*2+(-1)*4 } { -3 -4 }
| 5 7 | * { 1 2 } = | 5*1+7*3 5*2+7*4 | = | 26 38 |
{-2 8 } { 3 4 } {-2*1+8*3 -2*2+8*4 } { 22 28 }
此外,矩阵乘法并不满足交换律。
2.4.3 矩阵转置
矩阵转置由矩阵的行列元素颠倒得到,即:原有的行元素成为列元素;列元素成为行元素。
对于矩阵的积,转置遵循以下规则:(AB)T=BTAT
2.4.4 矩阵的秩
对于方阵,可以组合矩阵单元以生成数,称为秩。秩的定义是递归的。
Ex:一个2*2矩阵,二价秩的定义为:
| a11 a12 |
| a21 a22 | = a11*a22-a12*a21
借助较低的秩可以计算较高的秩。计算3价以上的秩的时候可以以n x n矩阵的任意k列,按以下公式计算:
n
det A= ∑ (-1)j+k ajkdetAjk
j=1
detA∫k是从矩阵A删掉第j行和第k列得到的子矩阵.
当计算大矩阵的秩,通常采用数值法。计算秩的一种途径是把矩阵分解成两个因子 A=LU,矩阵L在对角线上的所有元素为0,而矩阵U在对角线以下的所有元素为0 , 计算L和U的积,两积相乘就可以得到detA,
该方法是基于秩的如下特征:det(AB)=(detA)(detB)
对于秩不太理解的地方,可以等后面用到时候以实例做参照理解。
2.4.5 矩阵的逆矩阵
对于方阵当且仅当矩阵的秩不为0的时候,我们可以得到它的逆矩阵,一个n x n矩阵的逆矩阵记作A-1,且AA-1=A-1A=I
I为单位矩阵,其对角线元素为1,其余为0。
逆矩阵A-1的元素,可以从A的元素计算得来:
ajk-1 ={ (-1)j+k detAjk } / detA
ajk-1是A-1第j行和第k列的单元 , 而Ajk 是从A删去第j行和第k列得到的子矩阵。
来看一个例子:
考虑等式p’= pR 并且假设我们知道p’和R想求p。首先找到R–1,一旦求得R–1,我们便能求出p,就象这样:
由上,简单总结下逆矩阵:
● 只有正方形的矩阵(方阵)才能求逆,因此当我们说矩阵求逆,那么它就是方矩阵。
● n×n矩阵A的逆矩阵是一个n×n矩阵表示为A–1
● 不是每个方矩阵都逆矩阵
● 矩阵和它的逆矩阵相乘得到一个单位矩阵:A A–1 = A–1A = I。注意当我们进行这样的操作时矩阵是可交换的。
2.4.6 矩阵与D3D
在D3D中表示1×4的行向量,我们用D3DXVECTOR3和D3DXVECTOR4向量类。当然D3DXVECTOR3只3个成员,不是4个。然而,第4个成员缺省是1或0。
D3D表示4×4矩阵,用D3DXMATRIX类:
1 typedef struct D3DXMATRIX : public D3DMATRIX {
2 public :
3 D3DXMATRIX() {};
4 D3DXMATRIX( CONST FLOAT * );
5 D3DXMATRIX( CONST D3DMATRIX & );
6 D3DXMATRIX( FLOAT _11, FLOAT _12, FLOAT _13, FLOAT _14,
7 FLOAT _21, FLOAT _22, FLOAT _23, FLOAT _24,
8 FLOAT _31, FLOAT _32, FLOAT _33, FLOAT _34,
9 FLOAT _41, FLOAT _42, FLOAT _43, FLOAT _44 );
10 // access grants
11 FLOAT & operator () ( UINT Row, UINT Col );
12 FLOAT operator () ( UINT Row, UINT Col ) const ;
13
14 // casting operators
15 operator FLOAT * ();
16 operator CONST FLOAT * () const ;
17
18 // assignment operators
19 D3DXMATRIX & operator *= ( CONST D3DXMATRIX & );
20 D3DXMATRIX & operator += ( CONST D3DXMATRIX & );
21 D3DXMATRIX & operator -= ( CONST D3DXMATRIX & );
22 D3DXMATRIX & operator *= ( FLOAT );
23 D3DXMATRIX & operator /= ( FLOAT );
24
25 // unary operators
26 D3DXMATRIX operator + () const ;
27 D3DXMATRIX operator - () const ;
28
29 // binary operators
30 D3DXMATRIX operator * ( CONST D3DXMATRIX & ) const ;
31 D3DXMATRIX operator + ( CONST D3DXMATRIX & ) const ;
32 D3DXMATRIX operator - ( CONST D3DXMATRIX & ) const ;
33 D3DXMATRIX operator * ( FLOAT ) const ;
34 D3DXMATRIX operator / ( FLOAT ) const ;
35 friend D3DXMATRIX operator * ( FLOAT, CONST D3DXMATRIX & );
36 BOOL operator == ( CONST D3DXMATRIX & ) const ;
37 BOOL operator != ( CONST D3DXMATRIX & ) const ;
38 } D3DXMATRIX, * LPD3DXMATRIX;
39
40
41
42
43
44
45 //D3DXMATRIX类是从D3DMATRIX结构继承的:
46
47 typedef struct _D3DMATRIX {
48 union {
49 struct {
50 float _11, _12, _13, _14;
51 float _21, _22, _23, _24;
52 float _31, _32, _33, _34;
53 float _41, _42, _43, _44;
54 };
55 float m[ 4 ][ 4 ];
56 };
57 } D3DMATRIX;
58
59
D3DXMATRIX类可以发现很多运算符,如检测矩阵相等,相加减,与数相乘,铸造casting,以及非常重要的两个D3DXMATRIXs彼此相乘。
1 D3DXMATRIX A(…); // 初始化矩阵 A
2 D3DXMATRIX B(…); // 初始化矩阵 B
3 D3DXMATRIX C = A * B; // C = AB
D3DXMATRIX类另一个重要的运算符是小括号,它允许我们非常方便的为矩阵成员赋值。当用小括号时下标就象数组下标一样是从0开始的。例如,访问矩阵的第ij = 11 成员:
1 D3DXMATRIX M;
2 M( 0 , 0 ) = 5.0f ; // 设置入口 ij = 11 to 5.0f.
D3D库也提供了一些函数:如将D3DXMATRIX转化为单位矩阵,转置D3DXMATRIX矩阵及求逆矩阵。
1 D3DXMATRIX * D3DXMatrixIdentity(
2 D3DXMATRIX * pout
3 );
4
5 // 参数:
6
7 // pOut 指向D3DXMATRIX结构的返回单位矩阵。
8
9 // 返回值:
10
11 // 指向D3DXMATRIX 结构的单位矩阵。
12
13 D3DXMATRIX M;
14 D3DXMatrixIdentity( & M ); // M = 单位矩阵
15
16 D3DXMATRIX * D3DXMatrixTranspose(
17 D3DXMATRIX * pOut,
18 CONST D3DXMATRIX * pM
19 );
20
21 // 参数:
22 // pOut
23 // 指向D3DXMATRIX 结构的操作结果矩阵。
24 // pM
25 // 指向D3DXMATRIX 结构的源矩阵。
26 // 返回值:
27 // 指向D3DXMATRIX 结构的转置矩阵。
28
29 // 说明:
30 // 函数返回值跟pOut 参数返回值是一样的。这样可以让函数D3DXMatrixTranspose作为其它函数的参数使用。
31
32
33 D3DXMATRIX A(...); // initialize A
34 D3DXMATRIX B;
35 D3DXMatrixTranspose( & B, & A ); // B = transpose(A)
36
37 D3DXMATRIX * D3DXMatrixInverse(
38 D3DXMATRIX * pOut,
39 FLOAT * pDeterminant,
40 CONST D3DXMATRIX * pM
41 );
42
43 // 参数:
44 // pOut
45 // 指向D3DXMATRIX结构的逆矩阵。
46 // pDeterminant
47 // 指向FLOAT 类型的对角线[1,1][2,2][3,3][4,4]积,如果不需要,可以设置为 NULL。
48 // pM
49 // 指向 D3DXMATRIX 结构源矩阵。
50
51 // 返回值:
52 // 指向D3DXMATRIX 结构的逆矩阵。如果没有逆矩阵,就返回NULL值。
53 // 返回值是跟pOut 参数的返回值是一样的,这样可以让本函数成为其它函数的参数。
54
55
56
57
假如我们将不能求逆的矩阵用求逆函数,那么函数将会返回null.同样的,这本书我们忽视第二个参数,并且总是把它设置为0。
1 D3DXMATRIX A(...); // 初始化 A
2 D3DXMATRIX B;
3 D3DXMatrixInverse( & B, 0 , & A ); // B = 逆(A)