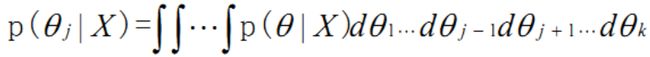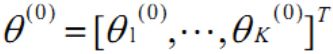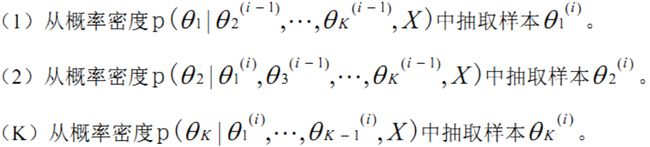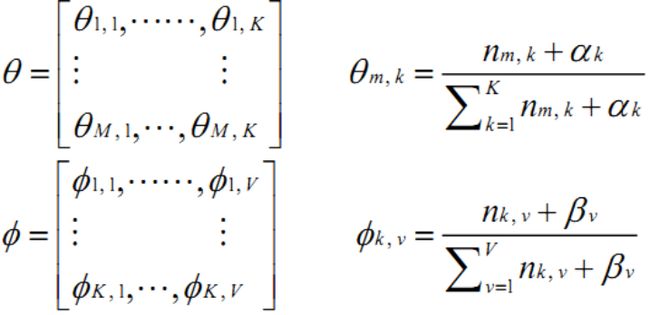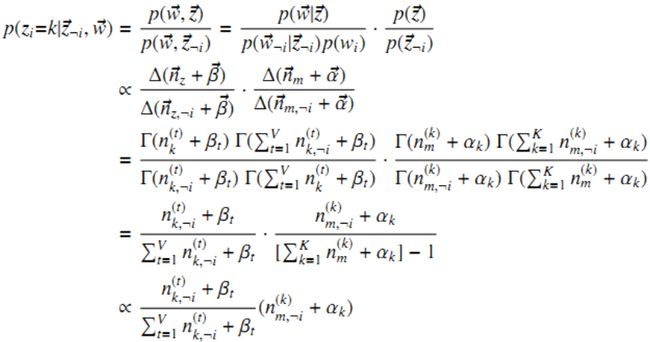lda主题模型
其实这篇文章也可以叫gibbs抽样在lda主题模型中的应用。lda里的重头戏就是gibbs抽样。话说现在论文起名字也是技术活儿,一般人还把握不好,一样的内容起个不同的名字,被reject的几率有时还真不一样。
lda主题模型又是一个有深厚数学背景的算法。
主题模型(topic model)是一种使用概率的产生式模型来挖掘文本主题的新方法。Topic Model中假设,主题可以根据一定的规则生成单词,那么在已经知道文本单词的情况下,可以通过概率方法反推出文本集的主题分布情况。
LDA相当于一种有向概率图模型,通过建立一个“文档一主题一单词”3层的贝叶斯模型,然后运用概率方法对模型进行推导,来寻找文本集的语义结构,挖掘文本的主题。
LDA将每个文档表示为一个主题混合,每个主题是固定词表上的一个多项式分布.LDA假设词由一个主题混合产生,同时每个主题是在固定词表上的一个多项式分布;这些主题被集合中的所有文档所共享;每个文档有一个特定的主题比例,从Diriehlet分布中抽样产生.
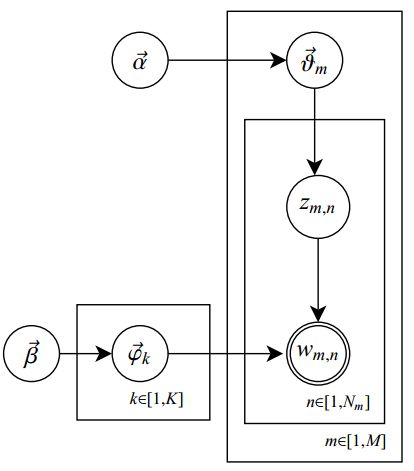
文档数量为M,单词索引数为N,主题数为K,zm,n表示文档m中第n个单词的主题,wm,n表示文档m中第n个单词,beta是每个Topic下单词的多项分布的Dirichlet先验参数,alpha是每个文档下Topic的多项分布的Dirichlet先验参数,θ为主题分布,φ为词分布,θmk表示文档m中主题k的dirichlet 分布,φkv表示单词v对于主题k的dirichlet分布。
现在有三种常用LDA模型推导方法:吉布斯抽样、变分贝叶斯、期望值传播。这里讲gibbs抽样。
gibbs抽样
吉布斯抽样算法是一种特殊的马尔科夫链蒙特卡洛方法(markov chain monte carlo,MCMC)。MCMC是一套从复杂的概率分布中抽取样本值的近似迭代方法,目的是提供一种参数后验分布中抽取样本的机制。
吉布斯抽样法是一种比较特殊的用于实现多重积分的 MCMC 算法,该方法的基本想是模拟一个马尔可夫链使得其分布为所要求的分布p(θ|X),然后用抽样估计参数,从而简化了多重积分的实现过程,降低了计算量。
令 θ=[θ1,...,θk]T表示未知参数的向量,X表示所采集的数据。假设所要求的为基于X的某些未知参数的边缘概率密度,即
p(θj | X),1≤j ≤ K,直接的求解方法是对联合概率密度中其他未知参数进行积分,即
大多数情况下,当未知参数维数K较大时,这种积分在计算上是很难实现的。吉布斯采样法的基本思想是对联合概率密度p(X|θ)进行随机采样然后利用这些随机样本来估计边缘概率密度。
吉布斯采样算法的具体过程如下:
通常情况下,采样所得的样本向量序列...,θ(i-1),θ(i),θ(i+1),...是一个马尔可夫链。当n足够大时,吉布斯采样方法得到的的p(X|θ)将收敛于
在lda主题模型中,需要估计的就是θ和φ。
nkv表示单词v指派给主题k的次数;nmk表示主题k出现在文档m中的次数,通过吉布斯抽样可以近似估计。
beta可理解为在见到语料库的任何词汇之前,从主题抽样获得的词汇出现频数。
alpha可以理解为,在见到任何文档文字之前,主题被抽样的频数。
尽管beta和alpha的具体取值会影响到主题及词汇被利用的程度,但不同的主题被利用的方式几乎没有变化,不同的词汇
被利用的方式也基本相同,因此可以假定对称的dirichlet分布,即所有的beta取相同的值,所有的alpha取相同的值。
排除当前词的主题分配,根据其他所有词的主题分配估计当前词分配各个主题的概率
具体证明就不在这里推导了。上式就是lda主题模型中gibbs抽样构造的马尔科夫链。
其具体的实现过程如下。
(1) zi被初始化为1到K之间的某个随机整数。即将文档中的词汇指派为任意一个主题。i从1循环到V ,V 是语料库中所有出现于文本中的词汇记号个数。此为 Markov 链的初始状态。
(2)根据公式(1)将词汇分配给主题,获取马尔科夫链的下一个状态。
(3) 迭代第(2)步足够次数以后,认为马尔科夫链接近目标分布,遂取 (i从1循环到V )的当前值作为样本记录下来。为了保证自相关较小,每迭代一定次数,记录其他的样本。
当链更新时,nkv和nmk也在不断更新。经过一定次数的迭代,最终达到抽样结果稳定,以nkv和nmk的值可以计算求得φkv和θmk 。
整个lda模型并不是特别复杂,难在数学推导的证明,下面我会给出一个简单的实现。
参考:http://blog.csdn.net/v_july_v/article/details/41209515
http://blog.csdn.net/yangliuy/article/details/8302599
Parameter estimation for text analysis--Gregor Heinrich