致佳音: 推箱子游戏自动求解算法设计(四)
这一节是本文的核心内容,即推箱子游戏求解算法的设计思路过程
前面已经说过过,判断局面重复的最好标准不是局面完全一致,而是坐标排序相同且角色坐标通行
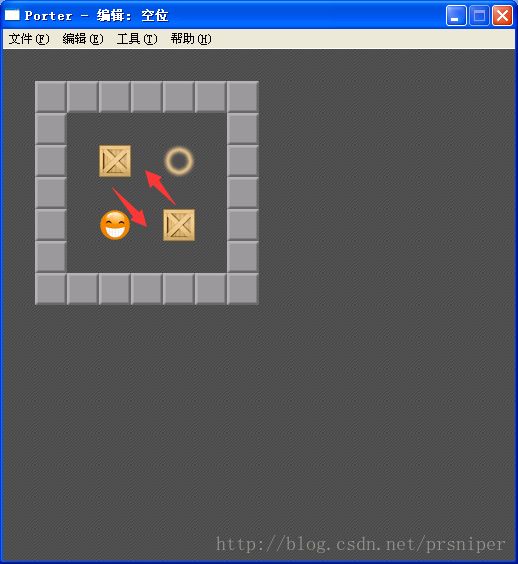
如下图,角色无论怎么移动,不推动箱子的时候,都能回到原来的位置,算作同一个局面:
再如下图,两个箱子互换位置,结果与没有移动箱子是一样的,所以排序箱子坐标以后一致,还是相同局面
问:有必要判断局面重复吗?是不是只是提升一下效率?
答:不是为了提升效率,而是为了能解出来,如果使用递归,重复的局面反复耗尽堆栈,而队列则耗尽内存
正如上图,反复推这两个箱子往返。
问:排序所有箱子再比较,也太鸡肋了,有没精髓?
答:有,那就是哈希表,不过哈希表有一丝隐隐的风险,那就是如果计算结果哈希不同,那么两团棉花数据肯定不同
但是如果结果相同,两团棉花数据也可能不同,当然相同数据长度不同数据哈希相同的概率极其低,像MD5那样把数
据长度加进去哈希的,重复就更加低,把地球的沙子都哈希一遍可能也就几颗重复,为了速度,我使用CRC32
问:那么,有了上面的基础,把搬运工向四个方向移动生成快照,然后递归下去就行了吗?
答:理论上是可以的,不过如上面所说,搬运工不推动箱子的时候,没有意义,属于闲走,我们的对象应该转移到箱子
上,而不是搬运工。把每个箱子向四个方向推动都生成快照,过滤重复,并“递归”直到所有的箱子归位
综上所述,我们就可以开始动工了,给个小问题思考,得到解法后,会不会还有更好的解法?或者换个问法:队列的处理如何进行?
我的方案是:先入先出,即先加入队列的先处理,这样保证更低步数的快照,先被分析,更低的步数当然是更好的解法,最终第一个
解法自然是最优解法……
场景数据结构:
#pragma pack(4) // STAR.Value(__int64)默认以64位对齐
typedef struct tagStage{
UINT Volume; // 结构体实际大小(加速计算)
UINT Flags; // 场景标识
PSTAR Stars; // 箱子位置列表(内部指针, 不释放, 数量为.Count)
PSTAR Series; // 排序箱子坐标(内部指针, 不释放, 数量为.Count)
UINT Count; // 箱子数量(目标数量)
UINT Value; // 归位数量
UINT Hash; // 场景指纹(箱子坐标排序哈希值)
tagStage *Prev; // 上个场景(游戏中连接队列操作, 伪指针, 不释放)
tagStage *Next; // 下个场景(游戏中连接队列操作, 伪指针, 不释放)
tagStage *Host; // 父级场景(求解时反向父级搜索得到解法路径, 伪指针, 不释放)
union {
STAR Size; // 场景尺寸
struct {
long SizeX; // 场景宽度(列数)
long SizeY; // 场景高度(行数)
};
};
union {
STAR Position; // 角色当前位置
struct {
long PosX; // 角色水平位置
long PosY; // 角色垂直位置
};
};
union {
STAR Automation; // 自动寻路位置
struct {
long AutoX; // 寻路水平坐标
long AutoY; // 寻路垂直坐标
};
};
PMOVE Moves; // 可行走法列表(内部指针, 不释放, 数量为.Count * 4: 四个方向)
UINT Range; // 可行走法数量
UINT Index; // 当前测试走法
UINT Slaves; // 剩余未分析的子场景数量
UINT Layer; // 当前步数
union {
BYTE Matrix[1]; // 矩阵数据
long Data;
};
} STAGE, *PSTAGE;
#pragma pack()
其中的内部指针指向结构体内部,比如Stars指向各个箱子的坐标,而不用转换Matrix再计算偏移,我们用32位内存,换取20多条汇编指令
一个刺客换一个王朝,,,好快的剑……
STAR是AlphaStar算法的数据结构,是一个坐标对
typedef union tagStar{ // Point type(8B)
struct {
long X;
long Y;
};
__int64 Value;
} STAR, *PSTAR;
Move是走法信息,记录了某种走法所影响到的数据,占48个字节,也存储与结构体内部,限于篇幅这里就不详述
然后是队列数据结构:
typedef struct tagQueue{ // 与堆栈不同, 先进先出
UINT Volume; // 队列容量(字节数)
UINT Size; // 元素内存大小
UINT Count; // 元素上限索引
UINT Value; // 当前元素个数(下个索引)
UINT Used; // 已用元素个数
UINT Step; // 结果步数
PSTAGE Active; // 首个活动场景(从此弹出)
PSTAGE Backup; // 末尾活动场景(向此压入)
PSTAGE Stages; // 过期场景(压入弹出)
PSHOT Shots; // 失败快照列表(外部指针, 外部释放)
PSTACK Stacks; // 扫描坐标列表(外部指针, 外部释放)
union {
BYTE Dummy[1];
UINT Data;
};
} QUEUE, *PQUEUE;
解法的逻辑过程如下:
1.初始化队列,提取第一个场景到当前场景
2.当前场景所有箱子归位,函数返回
3.分析场景得到若干个新场景,过滤重复
4.过滤后新场景数量为零,场景无解,删除场景(可优化,见下一篇)
5.追加新场景到队列,分析队列下一个场景,重复2-4
6.队列场景数量为零,场景无解(或队列太小,内存不足)
根据上一级场景生成新场景的函数代码(其他代码见资源包,限于篇幅,这里不详细列出):
// 从队列中申请一个场景, 并以当前场景填充, 扫描后检测重复, 有效则追加到队列
PSTAGE fnStageNext(PQUEUE pQueue, PSTAGE pStage, int *pdwCode)
{
PSTAGE pNext; // 生成下一步场景
PMOVE pMove;
int dwRet;
pNext = fnQueueApply(pQueue);
if(pNext == NULL)
{
if(pdwCode) *pdwCode = 0; // 队列耗尽
fnStageCode(SEC_CACHE_NULL);
return NULL;
}
// 复制上级数据, 修正指针
V32Copy(pNext, pStage, pStage->Volume);
pNext->Host = pStage; // .Prev和.Next在丢弃前或加入队列时赋值
fnStagePtr(pNext); // 修正内部指针
// 根据当前动作, 推动场景
pMove = &pStage->Moves[pStage->Index];
#ifdef _DEBUG
//fnPrint("当前场景=0x%08X, 父级场景=0x%08X, 玩家=(%d, %d), 箱子:\r\n", pStage, pStage->Host, pStage->PosX, pStage->PosY);
//fnPrintBox(pStage);
//fnPrint("当前动作: 箱子%d移至(%d, %d), 玩家移至(%d, %d), 寻路坐标为(%d, %d).\r\n\r\n",
// pMove->Index, pMove->ObjX, pMove->ObjY, pMove->PortX, pMove->PortY, pMove->MoveX, pMove->MoveY);
#endif
fnStagePush(pNext, pMove, SMF_MOVE_NONE); // 应用走法
pNext->Range = 0; // 没有走法
pNext->Index = 0; // ...
pNext->Layer++; // 步数
// 扫描线填充可通行单元
if(pNext->PosX == 2 && pNext->PosY == 4)
{
dwRet = 0;
}
dwRet = fnStageScan(pQueue, pNext);
// 检验局面重复
pNext->Hash = fnStageHash(pNext->Stars, pNext->Series, pNext->Count); // 排序计算哈希
dwRet = fnStageLoop(pQueue, pNext);
if(dwRet != 0)
{
#ifdef _DEBUG
fnPrint("丢弃重复场景=0x%08X.\r\n", pStage);
#endif
pNext->Prev = NULL; // 孤立, 防止队列删除(场景尚未加入队列, 只追加到回收链表)
pNext->Next = NULL;
fnQueueRemove(pQueue, pNext); // 移除场景
if(pdwCode) *pdwCode = -1; // 重复局面
fnStageCode(SEC_ERROR_NONE); // 清零错误
return NULL;
}
// 函数返回
if(pdwCode) *pdwCode = 1;
return pNext;
}
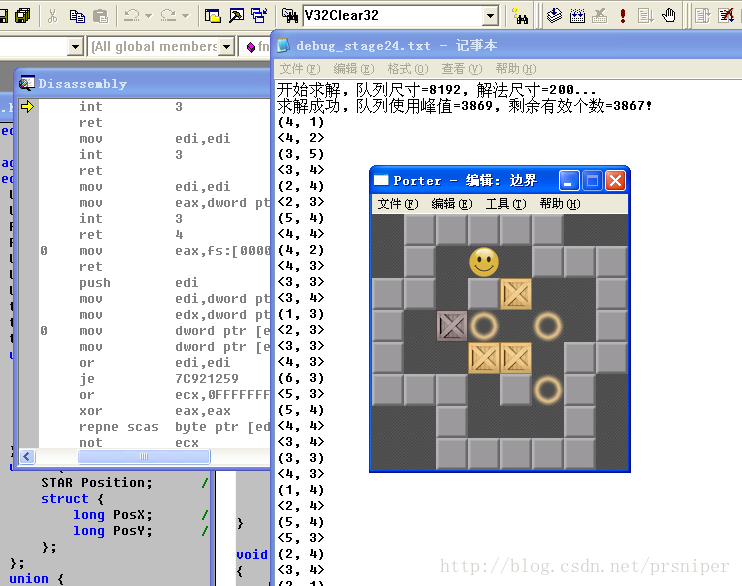
运行效果如图所示:
debug记录文件内容(下一节说说,程序的进一步优化,这个结果未经过优化):
开始求解, 队列尺寸=8192, 解法尺寸=200... 求解成功, 队列使用峰值=3869, 剩余有效个数=3867! (4, 1) <4, 2> (3, 5) <3, 4> (2, 4) <2, 3> (5, 4) <4, 4> (4, 2) <4, 3> <3, 3> <3, 4> (1, 3) <2, 3> <3, 3> <4, 3> (6, 3) <5, 3> (5, 4) <4, 4> <3, 4> (3, 3) <4, 3> (1, 4) <2, 4> (5, 4) <5, 3> (2, 4) <3, 4> (2, 1) <2, 2> <2, 3> (3, 6) <3, 5> <3, 4> <4, 4> (1, 4) <2, 4> <3, 4> (6, 2) <5, 2> (4, 3) <3, 3> (5, 5) <5, 4> (3, 4) <4, 4> (1, 3) <2, 3> (4, 1) <4, 2> <4, 3> <3, 3> (2, 4) <2, 3> (6, 3) <5, 3> <4, 3> <3, 3> (5, 5) <5, 4> (3, 4) <4, 4> (6, 3) <5, 3> <5, 4> (3, 3) <4, 3> (1, 3) <2, 3> (2, 1) <2, 2> 最优解法推动 43 次, 寻路 29 次, 合计坐标 72 个!