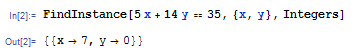扩展欧几里得算法是干什么用的?
扩展欧几里得算法(又称扩充欧几里得算法)是用来解某一类特定的不定方程的。讲解清楚需要好些预备知识,各位读者不能着急。我是花了半天时间来理解它。
不定方程
不定方程是以x,y为变量,形如ax+by=c,且a,b,x,y,c都为整数的一类方程。例如4x+5y=13,以不定方程来解,得x=-13, y=13。不定方程这个名词多见于小学中学,它还有个名词叫丢番图方程,这个名称似乎在学术界更为多见。
因子
![]() 表示a是b的因子,b是a的倍数。
表示a是b的因子,b是a的倍数。
不定方程有整数解
ax+by=c有整数解,当且仅当gcd(a,b)|c。详情见维基百科的贝祖定理条目。
例如,5x+14y=35有没有整数解呢?
贝祖定理告诉我们有!因为gcd(5,14)=1|35。
Mathematica告诉我们x=7, y=0。(你也可以手算。)
两个不定方程(扩展欧几里得算法作用之处)
定理:若ax+by=g,(g=gcd(a,b),即g是a,b的最大公约数)有整数解![]() ;则ax+by=c(c是g的倍数)有整数解
;则ax+by=c(c是g的倍数)有整数解![]() 。读者可以测试、证明一下。
。读者可以测试、证明一下。
设ExtendedGCD为扩展欧几里得算法,它接受两个整数a,b,返回两个整数x,y。
若有ax+by=gcd(a,b),则ExtendedGCD(a,b)可求x,y。
练习1
现在练习一下,使用ExtendedGCD,求6x+10y=2的整数解。
发现gcd(6,10)=2,2是6和10的最大公约数,于是求6x+10y=2的整数解可以用扩展欧几里得算法求。
以Mathematica代码为例:
所以x=2, y=-1。6×2+10×-1=12-10=2。
练习2
求9x+8y=2的整数解。
发现gcd(9,8)=1≠2,不能直接用扩展欧几里得算法。
根据上面所说的定理,先求9x+8y=gcd(9,8)的整数解。
所以9×1+8×-1=gcd(9,8)=1。
根据定理,ax+by=c有整数解![]() ,所以9x+8y=2有整数解
,所以9x+8y=2有整数解![]() 。
。
用来求模反元素
求a关于模n的模反元素(a<n)。egcd(a,n)={g,x,y}。若g=1,则该模反元素存在,为x;若g不等于1,则该模反元素不存在。注意,余数可以为负数的,相见维基百科。如果x为负,人们喜欢把它“正过来”,即再加上n。
练习
求540关于1769的模反元素。借助Mathematica的ExtendedGCD函数,得该模反元素为1769-95=1674。
容易验证540*1674 mod 1769=1。
求5关于17的模反元素。
In:= ExtendedGCD[5,17]
Out:= {1, {7, -2}}
答案为7。(不用加上n了)
希望对读者有帮助。
本文依照知识共享-署名-相同方式共享3.0协议释出
作者爱让一切都对了