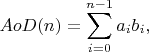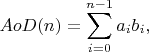【题目】【分析】本题较为简单,设置一个计数器,当接收的字符为"("时候自增,为")"时自减,为B时候退出循环。AC的C++代码如下:#include#includeusingnamespacestd;intmain(){strings;intcount;while(getline(cin,s)){count=0;intlen=s.length();for(inti=0;i
【算法随笔:HDU 3333 Turing tree】(线段树 | 离线 | 离散化 | 贪心)
XNB's Not a Beginner
算法算法哈希算法leetcodec++排序算法
https://acm.hdu.edu.cn/showproblem.php?pid=3333https://acm.hdu.edu.cn/showproblem.php?pid=3333https://vjudge.net.cn/problem/HDU-3333https://vjudge.net.cn/problem/HDU-3333题目很简单,给出长度为N的数组,Q次询问,每次给出区间[x,
test_Time_2h
爱思考的小伙
#基础数据结构与算法图论算法c++
文章目录RelicDiscoveryHDU-5982TextReverseHDU-1062DownloadManagerHDU-3233看病要排队HDU-1873RedandBlackHDU-1312最短路HDU-2544https://vjudge.csgrandeur.cn/contest/499778RelicDiscoveryHDU-5982#include#includeusingnam
hdu 4408 Minimum Spanning Tree
luckycoding
hdu
题目连接:点击打开链接解法:利用kruskal算法把图划分成森林,同一点有相同最小的权值到别的点,通过determinant计算树的课数。总结:模板+自己不太懂=记录+重新学代码君:#include#include#include#defineLLlonglongusingnamespacestd;constintMAX=105;constintMAXE=1005;structnode{intse
2024/2/17 图论 最短路入门 dijkstra 1
极度的坦诚就是无坚不摧
寒假集训寒假算法图论算法c++c语言dijkstra
目录算法思路Dijkstra求最短路AcWing849.Dijkstra求最短路I-AcWing850.Dijkstra求最短路II-AcWing题库最短路最短路-HDU2544-VirtualJudge(vjudge.net)【模板】单源最短路径(弱化版)P3371【模板】单源最短路径(弱化版)-洛谷|计算机科学教育新生态(luogu.com.cn)【模板】单源最短路径(标准版)P4779【模板
2048
不绝_7647
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2048思路:该题运用了错排公式,即D(n)=(n-1)*(D(n-1)+D(n-2))。计算出n张字条错排给n个人的可能性(每个人得到的都非自己的字条),再除以n张字条给n个人的所有可能性,就能得出结果。做法:建立数组a,并给a[0],a[1].a[2],a[3]分别赋值0,0,1,2.(其中1和2对应
杭电Oj第二周
J_4d20
做题有个习惯,就是没通过一道题之后都会找下答案,对比一下我的代码还有没有可以在优化的地方,使他更简便链接:http://acm.hdu.edu.cn/showproblem.php?pid=2016我的代码是:#includeintmain(){intn,a[100],t,i,b;while(scanf("%d",&n)!=EOF){if(na[j]){t=a[j];min=j;}for(i=1;
Smiles to the death(3)
KevinZucker
Oneday,a60-year-oldmanexperiencedchestpainandshortnessofbreathduetoexcessiveactivity.Hiswife,whoismorethan10yearshisjunior,wasalarmedatthesightofherhusbandandrushedtomassagehiminanattempttoincreasehis
任意IOS16系统iPad/Iphone开启台前调度
zxfBdd
工作效率ipadiphoneios
方法来自GitHub:GitHub-khanhduytran0/TrollPad:TrollSpringBoardintothinkingit'srunningoniPadOS注意操作前iPad/iPhone上需要安装巨魔手机助手和Filza,关于这两个软件的安装自行百度方法。备注一个巨魔手机助手的下载地址ReleaseTrollStar1.2·34306/TrollStar·GitHub原文内容
K8S之运用节点选择器指定Pod运行的节点
sissie喵~
kuberneteskubernetes容器云原生
node节点选择器的使用使用场景实践使用nodeName使用nodeSelectornodeName和nodeSelector混合使用1、设置了nodeName和设置Node上都不存在的标签。看调度情况2、设置nodeName为node1和设置node2上才有的标签。看调度情况实践总结使用场景默认情况,在创建Pod资源的时候,会根据schduler进行节点调度,默认会随机调度一个工作节点。如果想要
HDU 5159 Card 一次中出现两个也叫一次
DBWG
HDU算法
Problem-5159set暴力超时:intans=0,si=0;intx,b;voiddfs(setcur,intt){if(t==0){for(autox:cur)ans+=x;si++;return;}for(inti=1;i>x>>b;for(inti=1;is;s.insert(i);dfs(s,b-1);}cout>t;for(inti=1;i总次数减去未出现的次数就是出现次数//(
iOS逆向之腾讯视频广告篇
暴躁键盘侠
本文章主要是实现在非越狱机上去掉腾讯视频广告的一个功能,仅供学习交流!!!一、获取褪壳app首先我们需要一个去壳的ipa文件,以前在PP助手可以下载。但是后来PP助手不能用了,也没找到其他地方下载,只能自己动手了。下面推荐三种去壳的方式:Clutchdumpdecryptedfrida-ios-dump。过程在此不多做赘述,下面是我的使用心得。Clutch:失败率比较高,对几个小app砸壳成功,对
java string sscanf_hdu1106 字符串水题strtok()&&strchr()&&sscanf()+atoi()使用
LTT卍
javastringsscanf
字符串的题目用库函数往往能大大简化代码量以hdu1106为例函数介绍strtok()原型:char*strtok(chars[],constchar*delim);功能:分解字符串为一组字符串。s为要分解的字符串,delim为分隔符字符串。例如:strtok("abc,def,ghi",","),最后可以分割成为abcdefghi.尤其在点分十进制的IP中提取应用较多。(注意delim里面的不能看
容斥原理基础例题(HDU 2204, HDU 3208, HDU 1796)
王大凤
ACM
HDU2204题目求[1,N](1≤N≤1018)(1\leN\le10^{18})(1≤N≤1018)之间能被表示成mkm^kmk的数的数量。容斥思想1018约等于26410^{18}约等于2^{64}1018约等于264预处理质数:intprime[20]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59};因为合数的话肯定已经包括在所在质因子的部
C语言题目:HDU - 1408 盐水的故事
guuuuug
蓝桥杯c语言蓝桥杯算法c#
题目描述挂盐水的时候,如果滴起来有规律,先是滴一滴,停一下;然后滴二滴,停一下;再滴三滴,停一下...,现在有一个问题:这瓶盐水一共有VUL毫升,每一滴是D毫升,每一滴的速度是一秒(假设最后一滴不到D毫升,则花费的时间也算一秒),停一下的时间也是一秒这瓶水什么时候能挂完呢?输入输入数据占一行,由VUL和D组成,其中0<D<VUL<5000。输出
HDUOJ 4738 Caocao‘s Bridges 题解 桥 割边 Tarjan
kaiserqzyue
算法题目c++算法图论
题目链接:HDUOJ4738Caocao’sBridges题目描述:给定一个无向图,你可以选择最多删除一条边,删除边的代价是边的边权(特殊地,删除一条边权为0的边的代价是1),问最小代价使得图不连通。如果无论如何图都是连通的,那么则输出-1。题解:题目也就是需要我们求一条桥边,这个桥边所拥有的边权最小。我们只需要求出所有的桥边,然后对边权取一个最小值即可(需要注意边权为0的边我们要将其变成边权为1
HDU1677 矩阵嵌套 DP 记忆化搜索 图 最长上升序列
JUNLONG2
矩阵嵌套题有两种解法第一种是用图,然后记忆化搜索若矩形i能被嵌入矩形j则G[i][j]为1,状态转移方程:dp(i)=max{dp(i),dp(j)+1}这题如果我用图来解会显示超时第二种排序,然后求最长上升序列按面积递减排序
【2022杭电多校1】2022“杭电杯”中国大学生算法设计超级联赛(1)
andyc_03
算法acm
2022“杭电杯”中国大学生算法设计超级联赛(1)hdu7138-71491001String利用exkmp把s的每个后缀与s的lcp求出来设后缀[i,n][i,n][i,n]和sss的lcplcplcp长度为xxx那么只有当i≤xi\lexi≤x时,会产生贡献,中间重合部分为kkk的倍数的时候有贡献找到第一个和最后一个kkk的倍数的位置,把贡献差分一下即可#includeusingnamespa
杭电2055
NiRAutomata
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2055image.png思路:不难发现,这里a,b,c.....z呈现递增趋势分别对应相应的数字,而不是无规律的对应数字,那么我们就可以用ASCII码的加减转换,通过循环得到对应的所有值,再进行运算代码如下#includeintmain(void){intn,i,m,sum;chary;scanf("%
杭电HDU 3974Assign the task dfs出父包子的数组->知道管辖范围,线段树
DBWG
HDU深度优先算法
题目链接:Problem-3974(hdu.edu.cn)别的题解那对数的输入有点复杂,而且不用。。本题不讲线段树原理,会线段树后来看即可。思路:我们建好树,对树dfs。就题目样例吧:(建树网站:CSAcademy)每个节点进的时候记录,出的时候也记录,dfs完是这个效果节点//2344113552下标//12345678910比如start数组记录该点左下标start[2]=1end数组记录右下
iOS之removeFromSuperview遇到的坑:第二次执行animateWithDuration动画,没有动画效果
CoderZb
直接先附上有问题的效果101.175515.gif原因:我懒加载创建的view,而removeFromSuperview不是真正的移除view,所以view还存在,只是被隐藏了。因此第二次并不会再次懒加载创建view。所以第二次没有动画是因为,第一次最后停留的位置BBB,和第二次的位置是一模一样的。所以第二次移动之前,利用代码AAA更新一下frame就可以了(将view更新到屏幕底部)详情代码//
hdu(2680) 最短路径技巧
不给赞就别想跑哼
选择最佳路线时间限制:2000/1000MS(Java/Others)内存限制:32768/32768K(Java/Others)总提交内容:18613接受提交内容:6025问题描述有一天,琪琪想去拜访她的一个朋友。由于她很容易晕车,她想尽快到她朋友家。现在给你一张城市交通路线的地图,以及靠近Kiki家的车站,以便她可以乘坐。您可以认为Kiki可以在任何车站更换公交车。请找出Kiki需要花费的最少
【论文复现】DCFace: Synthetic Face Generation with Dual Condition Diffusion Model
李加号pluuuus
python人工智能机器学习
DCFace:用双条件扩散模型生成合成人脸。CVPR2023.4code:mk-minchul/dcface(github.com)paper:[2304.07060]DCFace:SyntheticFaceGenerationwithDualConditionDiffusionModel(arxiv.org)论文介绍应用:生成用于训练人脸识别模型的合成数据集。背景:生成合成数据集需要考虑多个因素
hdu 4734 F(x)
吵闹的人群保持笑容多冷静
算法c++动态规划
F(x)题意定义一个十进制数的权重:F(x)=xn⋅2n−1+xn−1⋅2n−2+...+x1⋅20F(x)=x_n\cdot2^{n-1}+x_{n-1}\cdot2^{n-2}+...+x_1\cdot2^0F(x)=xn⋅2n−1+xn−1⋅2n−2+...+x1⋅20给定两个数A,BA,BA,B,求出[0,B][0,B][0,B]中有多少个数的权重不大于AAA的权重思路可以发现权重最大为9
iOS动画中的枚举UIViewAnimationOptions
香橙柚子
首先这个枚举属于UIViewAnimation。我们经常使用的函数是[UIViewanimateWithDuration:animations:^{}completion:^(BOOLfinished){}];和[UIViewanimateWithDuration:animations:^{}];如果动画稍微复杂点,例如需要组合等等就可能用到这个函数:[UIViewanimateWithDurat
What made me change my mind about studying chemistry?
淑华_6c8b
Whatmademechangemymindaboutstudyingchemistry?WhydidIdecidetolearnandteachEnglishduringcollege?Inmyopinion,theyareaquestion,asamequestion.Ilikemakingdream.Butchemistryisnotaboutadream.It'sabouttruth,re
继之前的线程循环加到窗口中运行
3213213333332132
javathreadJFrameJPanel
之前写了有关java线程的循环执行和结束,因为想制作成exe文件,想把执行的效果加到窗口上,所以就结合了JFrame和JPanel写了这个程序,这里直接贴出代码,在窗口上运行的效果下面有附图。
package thread;
import java.awt.Graphics;
import java.text.SimpleDateFormat;
import java.util
linux 常用命令
BlueSkator
linux命令
1.grep
相信这个命令可以说是大家最常用的命令之一了。尤其是查询生产环境的日志,这个命令绝对是必不可少的。
但之前总是习惯于使用 (grep -n 关键字 文件名 )查出关键字以及该关键字所在的行数,然后再用 (sed -n '100,200p' 文件名),去查出该关键字之后的日志内容。
但其实还有更简便的办法,就是用(grep -B n、-A n、-C n 关键
php heredoc原文档和nowdoc语法
dcj3sjt126com
PHPheredocnowdoc
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8">
<title>Current To-Do List</title>
</head>
<body>
<?
overflow的属性
周华华
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
《我所了解的Java》——总体目录
g21121
java
准备用一年左右时间写一个系列的文章《我所了解的Java》,目录及内容会不断完善及调整。
在编写相关内容时难免出现笔误、代码无法执行、名词理解错误等,请大家及时指出,我会第一时间更正。
&n
[简单]docx4j常用方法小结
53873039oycg
docx
本代码基于docx4j-3.2.0,在office word 2007上测试通过。代码如下:
import java.io.File;
import java.io.FileInputStream;
import ja
Spring配置学习
云端月影
spring配置
首先来看一个标准的Spring配置文件 applicationContext.xml
<?xml version="1.0" encoding="UTF-8"?>
<beans xmlns="http://www.springframework.org/schema/beans"
xmlns:xsi=&q
Java新手入门的30个基本概念三
aijuans
java新手java 入门
17.Java中的每一个类都是从Object类扩展而来的。 18.object类中的equal和toString方法。 equal用于测试一个对象是否同另一个对象相等。 toString返回一个代表该对象的字符串,几乎每一个类都会重载该方法,以便返回当前状态的正确表示.(toString 方法是一个很重要的方法) 19.通用编程:任何类类型的所有值都可以同object类性的变量来代替。
《2008 IBM Rational 软件开发高峰论坛会议》小记
antonyup_2006
软件测试敏捷开发项目管理IBM活动
我一直想写些总结,用于交流和备忘,然都没提笔,今以一篇参加活动的感受小记开个头,呵呵!
其实参加《2008 IBM Rational 软件开发高峰论坛会议》是9月4号,那天刚好调休.但接着项目颇为忙,所以今天在中秋佳节的假期里整理了下.
参加这次活动是一个朋友给的一个邀请书,才知道有这样的一个活动,虽然现在项目暂时没用到IBM的解决方案,但觉的参与这样一个活动可以拓宽下视野和相关知识.
PL/SQL的过程编程,异常,声明变量,PL/SQL块
百合不是茶
PL/SQL的过程编程异常PL/SQL块声明变量
PL/SQL;
过程;
符号;
变量;
PL/SQL块;
输出;
异常;
PL/SQL 是过程语言(Procedural Language)与结构化查询语言(SQL)结合而成的编程语言PL/SQL 是对 SQL 的扩展,sql的执行时每次都要写操作
Mockito(三)--完整功能介绍
bijian1013
持续集成mockito单元测试
mockito官网:http://code.google.com/p/mockito/,打开documentation可以看到官方最新的文档资料。
一.使用mockito验证行为
//首先要import Mockito
import static org.mockito.Mockito.*;
//mo
精通Oracle10编程SQL(8)使用复合数据类型
bijian1013
oracle数据库plsql
/*
*使用复合数据类型
*/
--PL/SQL记录
--定义PL/SQL记录
--自定义PL/SQL记录
DECLARE
TYPE emp_record_type IS RECORD(
name emp.ename%TYPE,
salary emp.sal%TYPE,
dno emp.deptno%TYPE
);
emp_
【Linux常用命令一】grep命令
bit1129
Linux常用命令
grep命令格式
grep [option] pattern [file-list]
grep命令用于在指定的文件(一个或者多个,file-list)中查找包含模式串(pattern)的行,[option]用于控制grep命令的查找方式。
pattern可以是普通字符串,也可以是正则表达式,当查找的字符串包含正则表达式字符或者特
mybatis3入门学习笔记
白糖_
sqlibatisqqjdbc配置管理
MyBatis 的前身就是iBatis,是一个数据持久层(ORM)框架。 MyBatis 是支持普通 SQL 查询,存储过程和高级映射的优秀持久层框架。MyBatis对JDBC进行了一次很浅的封装。
以前也学过iBatis,因为MyBatis是iBatis的升级版本,最初以为改动应该不大,实际结果是MyBatis对配置文件进行了一些大的改动,使整个框架更加方便人性化。
Linux 命令神器:lsof 入门
ronin47
lsof
lsof是系统管理/安全的尤伯工具。我大多数时候用它来从系统获得与网络连接相关的信息,但那只是这个强大而又鲜为人知的应用的第一步。将这个工具称之为lsof真实名副其实,因为它是指“列出打开文件(lists openfiles)”。而有一点要切记,在Unix中一切(包括网络套接口)都是文件。
有趣的是,lsof也是有着最多
java实现两个大数相加,可能存在溢出。
bylijinnan
java实现
import java.math.BigInteger;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
public class BigIntegerAddition {
/**
* 题目:java实现两个大数相加,可能存在溢出。
* 如123456789 + 987654321
Kettle学习资料分享,附大神用Kettle的一套流程完成对整个数据库迁移方法
Kai_Ge
Kettle
Kettle学习资料分享
Kettle 3.2 使用说明书
目录
概述..........................................................................................................................................7
1.Kettle 资源库管
[货币与金融]钢之炼金术士
comsci
金融
自古以来,都有一些人在从事炼金术的工作.........但是很少有成功的
那么随着人类在理论物理和工程物理上面取得的一些突破性进展......
炼金术这个古老
Toast原来也可以多样化
dai_lm
androidtoast
Style 1: 默认
Toast def = Toast.makeText(this, "default", Toast.LENGTH_SHORT);
def.show();
Style 2: 顶部显示
Toast top = Toast.makeText(this, "top", Toast.LENGTH_SHORT);
t
java数据计算的几种解决方法3
datamachine
javahadoopibatisr-languer
4、iBatis
简单敏捷因此强大的数据计算层。和Hibernate不同,它鼓励写SQL,所以学习成本最低。同时它用最小的代价实现了计算脚本和JAVA代码的解耦,只用20%的代价就实现了hibernate 80%的功能,没实现的20%是计算脚本和数据库的解耦。
复杂计算环境是它的弱项,比如:分布式计算、复杂计算、非数据
向网页中插入透明Flash的方法和技巧
dcj3sjt126com
htmlWebFlash
将
Flash 作品插入网页的时候,我们有时候会需要将它设为透明,有时候我们需要在Flash的背面插入一些漂亮的图片,搭配出漂亮的效果……下面我们介绍一些将Flash插入网页中的一些透明的设置技巧。
一、Swf透明、无坐标控制 首先教大家最简单的插入Flash的代码,透明,无坐标控制: 注意wmode="transparent"是控制Flash是否透明
ios UICollectionView的使用
dcj3sjt126com
UICollectionView的使用有两种方法,一种是继承UICollectionViewController,这个Controller会自带一个UICollectionView;另外一种是作为一个视图放在普通的UIViewController里面。
个人更喜欢第二种。下面采用第二种方式简单介绍一下UICollectionView的使用。
1.UIViewController实现委托,代码如
Eos平台java公共逻辑
蕃薯耀
Eos平台java公共逻辑Eos平台java公共逻辑
Eos平台java公共逻辑
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年6月1日 17:20:4
SpringMVC4零配置--Web上下文配置【MvcConfig】
hanqunfeng
springmvc4
与SpringSecurity的配置类似,spring同样为我们提供了一个实现类WebMvcConfigurationSupport和一个注解@EnableWebMvc以帮助我们减少bean的声明。
applicationContext-MvcConfig.xml
<!-- 启用注解,并定义组件查找规则 ,mvc层只负责扫描@Controller -->
<
解决ie和其他浏览器poi下载excel文件名乱码
jackyrong
Excel
使用poi,做传统的excel导出,然后想在浏览器中,让用户选择另存为,保存用户下载的xls文件,这个时候,可能的是在ie下出现乱码(ie,9,10,11),但在firefox,chrome下没乱码,
因此必须综合判断,编写一个工具类:
/**
*
* @Title: pro
挥洒泪水的青春
lampcy
编程生活程序员
2015年2月28日,我辞职了,离开了相处一年的触控,转过身--挥洒掉泪水,毅然来到了兄弟连,背负着许多的不解、质疑——”你一个零基础、脑子又不聪明的人,还敢跨行业,选择Unity3D?“,”真是不自量力••••••“,”真是初生牛犊不怕虎•••••“,••••••我只是淡淡一笑,拎着行李----坐上了通向挥洒泪水的青春之地——兄弟连!
这就是我青春的分割线,不后悔,只会去用泪水浇灌——已经来到
稳增长之中国股市两点意见-----严控做空,建立涨跌停版停牌重组机制
nannan408
对于股市,我们国家的监管还是有点拼的,但始终拼不过飞流直下的恐慌,为什么呢?
笔者首先支持股市的监管。对于股市越管越荡的现象,笔者认为首先是做空力量超过了股市自身的升力,并且对于跌停停牌重组的快速反应还没建立好,上市公司对于股价下跌没有很好的利好支撑。
我们来看美国和香港是怎么应对股灾的。美国是靠禁止重要股票做空,在
动态设置iframe高度(iframe高度自适应)
Rainbow702
JavaScriptiframecontentDocument高度自适应局部刷新
如果需要对画面中的部分区域作局部刷新,大家可能都会想到使用ajax。
但有些情况下,须使用在页面中嵌入一个iframe来作局部刷新。
对于使用iframe的情况,发现有一个问题,就是iframe中的页面的高度可能会很高,但是外面页面并不会被iframe内部页面给撑开,如下面的结构:
<div id="content">
<div id=&quo
用Rapael做图表
tntxia
rap
function drawReport(paper,attr,data){
var width = attr.width;
var height = attr.height;
var max = 0;
&nbs
HTML5 bootstrap2网页兼容(支持IE10以下)
xiaoluode
html5bootstrap
<!DOCTYPE html>
<html>
<head lang="zh-CN">
<meta charset="UTF-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">