HDU 2971（数论，构造矩阵+矩阵乘法优化）

Tower

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 601    Accepted Submission(s): 154

Problem Description

Alan loves to construct the towers of building bricks. His towers consist of many cuboids with square base. All cuboids have the same height h = 1. Alan puts the consecutive cuboids one over another:

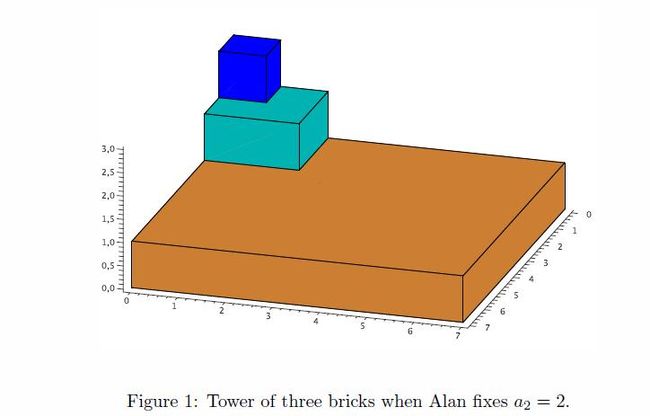
Recently in math class, the concept of volume was introduced to Alan. Consequently, he wants to compute the volume of his tower now. The lengths of cuboids bases (from top to bottom) are constructed by Alan in the following way:

1. Length a1 of the first square is one.

2. Next, Alan fixes the length a2 of the second square.

3. Next, Alan calculates the length an (n > 2) by 2*a2*(an-1)-(an-2). Do not ask why he chose such

a formula; let us just say that he is a really peculiar young fellow. For example, if Alan fixes a2 = 2, then a3 = 8 -a1 = 7; see Figure 1. If Alan fixes a2 = 1, then an = 1 holds for all n belong to N; see Figure 2.

Now Alan wonders if he can calculate the volume of tower of N consecutive building bricks. Help Alan and write the program that computes this volume. Since it can be quite large, it is enough to compute the answer modulo given natural number m.

 

 

Input

The input contains several test cases. The first line contains the number t (t <= 10^5) denoting the number of test cases. Then t test cases follow. Each of them is given in a separate line containing three integers a2,N,m (1 <= a2,m <= 10^9, 2 <= N <= 10^9) separated by a single space, where a2 denotes the fixed length of second square in step 2, while N denotes the number of bricks constructed by Alan.

 

 

Output

For each test case (a2,N,m) compute the volume of tower of N consecutive bricks constructed by Alan according to steps (1-3) and output its remainder modulo m.

 

 

Sample Input

   
   
   
   

    
    
    
    3
2 3 100
1 4 1000
3 3 1000000000
   
   
   
   

 

 

Sample Output

   
   
   
   

    
    
    
    54
4
299

   
   
   
   

 

 

 

先假设a2 = t, 题目给定了递推关系：An = 2 * t * An-1 - An-2 (n > 2)，初值A1 = 1, A2 = t；题目要求Sn = An ^ 2 + An-1 ^ 2 + ... + A1 ^ 2。
　　反复应用递推关系得到：
　　
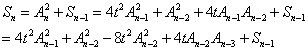
　　然后Sn-1利用相同的方式展开，把4tAn-2An-3约去，得到：
　　
　　这样就比较容易得出Sn的通项：
　　

#include <iostream> using namespace std; #define N 4 struct Mat { __int64 martix[N][N]; void clear() { memset(martix,0,sizeof(martix)); } }; __int64 MOD,a2,n; int a[5]; Mat res,q; Mat Martix_Mul(Mat &a,Mat &b) { int i,j,k; Mat c; c.clear(); for (i = 0;i < N;i++) for (j = 0;j < N;j++) { for (k = 0;k < N;k++) if (a.martix[i][k] && b.martix[k][j]) c.martix[i][j] = (c.martix[i][j] + a.martix[i][k] * b.martix[k][j]) % MOD; } return c; } int main() { int t,i,j; int sum; __int64 temp,temp1; scanf("%d",&t); while (t--) { scanf("%I64d%I64d%I64d",&a2,&n,&MOD); for(i=0;i<N;i++) { for (j=0;j<N;j++) { res.martix[i][j]=(i==j); } } q.clear(); temp=(a2*a2)%MOD; q.martix[1][0]=q.martix[2][1]=q.martix[3][2]=1; q.martix[0][0]=(4*temp)%MOD; q.martix[0][1]=(2-8*temp)%MOD; q.martix[0][2]=(4*temp)%MOD; q.martix[0][3]=-1; temp1=(2*a2*a2-1)%MOD; a[0]=0; a[1]=1; a[2]=(1+a2*a2)%MOD; a[3]=(a[2]+(temp1*temp1)%MOD)%MOD; if(n==2) { printf("%d/n",a[2]); continue; } else if(n==3) { printf("%d/n",a[3]); continue; } n-=3; while (n) { if(n&1) res=Martix_Mul(res,q); q=Martix_Mul(q,q); n>>=1; } sum=0; for (i=0;i<4;i++) { sum=(sum+(res.martix[0][i]*a[3-i])%MOD)%MOD; if(sum<0) sum+=MOD; } printf("%d/n",sum%MOD); } return 0; }