DP入门系列二--DAG之二最短路（硬币问题）

续上篇：http://blog.csdn.net/hu1020935219/article/details/12777635

引言：

DAG：有向无环图。

DAG是学习动态规划的基础，很多问题都可以直接转化为DAG上的最长路、最短路或路径计数问题。

两个经典的DAG模型，嵌套矩形和硬币问题，今天写第二个硬币模型问题。

这个问题我搞了两天才弄明白。。。

二、硬币问题

第二个DAG模型：硬币问题。

【问题描述】

有n种硬币，面值分别为V1，V2，V3，.....Vn，每种都有无限多。

给定非负整数S，可以选用多少个硬币，使得面值之和恰好为S？
输出硬币数目的最小值和最大值。1<=n>=100, 0<=S<=10000,1<=Vi<=S.

【分析与思路】
思路：本题是固定终点和起点的DAG动态规划。
我们把每种面值看做一个点，表示“还需要凑足的面值”，则初始状态为S，目标状态为0。
如当前在状态i，没使用一个硬币j，状态变转移到i-Vj。

【问题解析】

这个如果记忆化搜索的话可以参考上篇文章的。

这次我们还可以采用递推的。

代码是递推的。详细请看代码。

【最优字典序】

参考上篇

三、实例实践

假如我们要组成12分，我们有3，4，5分，三种硬币（将其分别编号1,2,3）

DAG图示，省略。。。

如果需要，请参考上篇自己画吧，

....................

刚刚再尝试画图的时候发现，这个例子有点坑爹，因为硬币的数目是无限个，，，，而且啊，上面的那个12分的，只用到了3分或者4分，，不过道理，大家都懂得吧。

【结果】

显然最长的路径为1--1--1--1， 即是4个3分

即是最长路为4，最长的路径为1--1--1--1

同理。

最短路径是2--2--2，最短路为3

附录：参考代码

/***** DAG之二硬币问题 ********/

/******** written by C_Shit_Hu ************/

////////////////动态规划///////////////

/****************************************************************************/
/* 
有n种硬币，面值分别为V1，V2，V3，.....Vn，每种都有无限多。
给定非负整数S，可以选用多少个硬币，使得面值之和恰好为S？
输出硬币数目的最小值和最大值。1<=n>=100, 0<=S<=10000,1<=Vi<=S.

思路：本题是固定终点和起点的DAG动态规划。
我们把每种面值看做一个点，表示“还需要凑足的面值”，则初始状态为S，目标状态为0。
如当前在状态i，没使用一个硬币j，状态变转移到i-Vj。
*/
/****************************************************************************/

#include<stdio.h>
#include<string.h>
#define MAX 10001
// #define long long int INf 1000000000;
#define INF  1000000000;
int n, S;
int V[MAX] ,vis[MAX], d[MAX];
int max[MAX], min[MAX] ;

// 记忆化搜索最长路程序
// 在主程序稍加修改后，调用即可
/*
int dp( int S)
{
	int i ;
	if ( vis[S]) 
		return d[S] ;
	vis[S] = 1;
	//int ans = d[S] ;
	d[S] = -1<<30 ;
	for (i=1; i<=n; i++ )
		if(S >= vis[i])
			d[S] = dp(S-V[i]) +1 ;
		return d[S] ;
}
*/


// 输出最小字典序
void prit_ans(int *d, int S)
{
	int i;
	for( i=1; i<=n; i++)
	if (S>=V[i] && d[S] == d[S-V[i]] +1)
	{
		printf("%d ", i);
		prit_ans(d, S-V[i]) ;
		break ;
	}
}

// 主函数、递推实现最短路最长路
int main ()
{
	memset(min,0,sizeof(min));  
	memset(max,0,sizeof(max));  
       memset(V,0,sizeof(V));  
	int i ,j ;
    min[0] = max[0] = 0;
	printf("请输入要组成的面值之和S：");
	scanf("%d", &S) ;
	printf("请输入不同面值的硬币的种类：");
	scanf("%d", &n) ;
	printf("请输入各个种类的硬币的面值：\n");
	for (i=1; i<=n; i++)
	{
		scanf("%d", &V[i]);
	}
    // 递推算法求解最长最短路 for (i=1; i<=S; i++) { min[i] = INF; max[i] = -INF; } for (i=1; i <= S; i++) for (j=1; j<=n; j++) if(i >= V[j]) { if (min[i] >= (min[i-V[j]] +1)) { min[i] = min[i-V[j]] +1; } if (max[i] <= (max[i-V[j]] +1)) { max[i] = max[i-V[j]] +1; } } printf("%d %d\n", min[S], max[S]);
	//	输出最优字典序
	prit_ans(min, S);
	printf("\n");
	prit_ans(max, S) ;
	printf("\n");

	return 0 ;
}


/******************************************************/
/********************  心得体会  **********************/
/*

*/
/******************************************************/

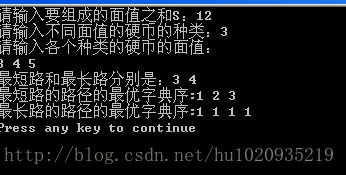
运行结果：