poj 2987 Firing 【最大权闭合图 输出点数和最大权值】
| Time Limit: 5000MS | Memory Limit: 131072K | |
| Total Submissions: 9006 | Accepted: 2707 |
Description
You’ve finally got mad at “the world’s most stupid” employees of yours and decided to do some firings. You’re now simply too mad to give response to questions like “Don’t you think it is an even more stupid decision to have signed them?”, yet calm enough to consider the potential profit and loss from firing a good portion of them. While getting rid of an employee will save your wage and bonus expenditure on him, termination of a contract before expiration costs you funds for compensation. If you fire an employee, you also fire all his underlings and the underlings of his underlings and those underlings’ underlings’ underlings… An employee may serve in several departments and his (direct or indirect) underlings in one department may be his boss in another department. Is your firing plan ready now?
Input
The input starts with two integers n (0 < n ≤ 5000) and m (0 ≤ m ≤ 60000) on the same line. Next follows n + m lines. The first n lines of these give the net profit/loss from firing the i-th employee individually bi (|bi| ≤ 107, 1 ≤ i ≤ n). The remaining m lines each contain two integers i and j (1 ≤ i, j ≤ n) meaning the i-th employee has the j-th employee as his direct underling.
Output
Output two integers separated by a single space: the minimum number of employees to fire to achieve the maximum profit, and the maximum profit.
Sample Input
5 5 8 -9 -20 12 -10 1 2 2 5 1 4 3 4 4 5
Sample Output
2 2
Hint
As of the situation described by the sample input, firing employees 4 and 5 will produce a net profit of 2, which is maximum.
题意:一个有N个员工的公司要裁员,已知若要裁掉员工A,就必须先裁掉他的党羽。现在已经给出裁掉每个员工可以得到的收益(可能正可能负)和M个关系——a b表示b是a的党羽。
问你1,裁掉的最少人数;2,可以获得的最大收益。
分析:明显的最大权闭合图,关键在于求出裁掉的最少人数。其实关于这个问题,在图构造出来后,就很明了了。
先说建图:设置超级源点source,超级汇点sink
1,source向所有裁掉得到正收益的员工建边,容量为正收益;
2,所有裁掉得到负收益的员工向sink建边,容量为负收益;
3,对于a b 即b是a的党羽,裁掉a则必须裁掉b,建边b -> a,容量为1;
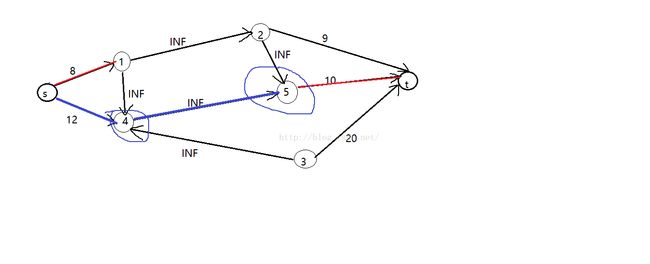
建图如下:
图中红色的边是最小割。从源点沿未满流边遍历的路线就是蓝色的边,遍历过程中得到的点集{4, 5}就是我们要找的最大权闭合图。
这样找最大权闭合图的点集——就是从源点开始,沿着残量网络中未满流的边遍历,整个过程中遍历到的所有点均是最大权闭合图中的点。
看神牛的证明!
命题: 根据闭合图定义建图G,在对图G运行最大流后,最大权闭合图V的势是唯一的.
证明:设两个最大全闭合图V1,V2,它们的权值相等,不失一般性,假设|V1|<|V2|.考虑以下情况:
1)若V1包含于V2,因为|V1|<|V2|,则V2-V1不等于空集.同时,不存在从V1到V2-V1的边,否则根闭合图定义矛盾.由于V1和V2的权值相同,则说明V2-V1的权值为0.根据最大权闭合图的求法以及运行过最大流可知,源点S不可能到达V2-V1.否则与V2-V1权值为0矛盾.进而,运行最大流以后,实际上只有|V1|大小的最大权闭合图.
2)若V1∩V2等于空集,则把V1和V2合并将产生一个更大的闭合图.因此,V1∩V2不等于空集,不妨记为S=V1∩V2,则不存在从S到V1-S或V2-S的边,若存在x属于V1-S,则对于V2来说,与闭合图定义矛盾,同理知V1.根据已知有,W(S)+W(V1-S)=W(S)+W(V2-S),即W(V1-S)=W(V2-S),若W(V1-S)>0,则将V1,V2合并会产生更大的闭合图,矛盾;若W(V1-S)<0,则将V1-S和V2-S去掉,使得S本身为一个闭合图,且它的权比V1或V2大,矛盾.因此W(V1-S)=W(V2-S)=0,由1)的证明知,从源点不可达V1-S或V2-S,因此,实际上得到的最大权闭合图就是S,其权值与V1,V2相同.
综上所述,运行最大流后,最大权闭合图的势是唯一的.
AC代码:
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define MAXN 6000
#define MAXM 200000
#define INF 0x3f3f3f3f3f
#define LL long long
using namespace std;
struct Edge
{
int from, to;
LL cap, flow;
int next;
};
Edge edge[MAXM];
int head[MAXN], edgenum;
int dist[MAXN], cur[MAXN];
bool vis[MAXN];
int N, M;
int source, sink;
LL sum;
void init()
{
edgenum = 0;
memset(head, -1, sizeof(head));
}
void addEdge(int u, int v, int w)
{
Edge E1 = {u, v, w, 0, head[u]};
edge[edgenum] = E1;
head[u] = edgenum++;
Edge E2 = {v, u, 0, 0, head[v]};
edge[edgenum] = E2;
head[v] = edgenum++;
}
void getMap()
{
int a, b;
source = 0, sink = N+1;
sum = 0;
for(int i = 1; i <= N; i++)
{
scanf("%d", &a);
if(a > 0)
addEdge(source, i, a), sum += a;
else
addEdge(i, sink, -a);
}
for(int i = 1; i <= M; i++)
{
scanf("%d%d", &a, &b);
addEdge(a, b, INF);
}
}
bool BFS(int s, int t)
{
queue<int> Q;
memset(dist, -1, sizeof(dist));
memset(vis, false, sizeof(vis));
dist[s] = 0;
vis[s] = true;
Q.push(s);
while(!Q.empty())
{
int u = Q.front();
Q.pop();
for(int i = head[u]; i != -1; i = edge[i].next)
{
Edge E = edge[i];
if(!vis[E.to] && E.cap > E.flow)
{
dist[E.to] = dist[u] + 1;
if(E.to == t) return true;
vis[E.to] = true;
Q.push(E.to);
}
}
}
return false;
}
LL DFS(int x, LL a, int t)
{
if(x == t || a == 0) return a;
LL flow = 0, f;
for(int &i = cur[x]; i != -1; i = edge[i].next)
{
Edge &E = edge[i];
if(dist[E.to] == dist[x] + 1 && (f = DFS(E.to, min(a, E.cap-E.flow), t)) > 0)
{
edge[i].flow += f;
edge[i^1].flow -= f;
flow += f;
a -= f;
if(a == 0) break;
}
}
return flow;
}
LL Maxflow(int s, int t)
{
LL flow = 0;
while(BFS(s, t))
{
memcpy(cur, head, sizeof(head));
flow += DFS(s, INF, t);
}
return flow;
}
int num;//最少人数
void find_S(int u)//在残量网络里面找源点能到点 就是最大权闭合图
{
num++;
vis[u] = true;
for(int i = head[u]; i != -1; i = edge[i].next)
{
Edge E = edge[i];
if(!vis[E.to] && E.cap > E.flow)
find_S(E.to);
}
}
int main()
{
while(scanf("%d%d", &N, &M) != EOF)
{
init();
getMap();
LL ans = sum - Maxflow(source, sink);//最大利润
num = 0;
memset(vis, false, sizeof(vis));
find_S(source);
printf("%d %lld\n", --num, ans);
}
return 0;
}