有向图强连通分量tarjan算法学习笔记
强连通分量的定义:
在一个图的子图中,任意两个点相互可达,也就是存在互通的路径,那么这个子图就是强连通分量(或者称为强连通分支)。如果一个有向图的任意两个点相互可达,那么这个图就称为强连通图。
tarjan算法基于dfs。而且每个强连通分量恰好是深搜树的一颗子树。
从网上了解到的tarjan算法的原理:
如果u是某个强连通分量的根,那么:
(1)u不存在路径可以返回到它的祖先
(2)u的子树也不存在路径可以返回到u的祖先。
直接这么看原理不好理解,接下来我慢慢来解释:
存储信息:DFN[i]标记i这个点被访问到的时间
low[i]表示i这个点直接或者间接可以到达的点里面最早被访问到的点的时间(实际上就是同一个强连通分量里的根)
步骤:从第1个点(u)开始搜索,刚开始要把DFN[u]和low[u]赋值为被访问到的时间, 每次都去遍历这个点关联的边<u,v>:
如果v不在栈里面,继续去递归搜索v,等到回溯以后,就要对low[u]判断,如果u的子树能到达更早的点,那么就把low[u]进行修改。
如果v已经在栈里面了,此时形成一个环,那么此时对于low[u]的修改就是:
if(low[u]>DFN[v])
low[u]=DFN[v];
这样很明显,只有强连通分量的根的DFN值和low值是相等的,其他的点都进行过修改,所以如果DFN[i]==low[i],说明我们找到了一个强连通分量的根,要得到这个强连通分量,只要把相应元素出栈就行了。
由于每个点只访问1次,每条边也是1次,所以tarjan算法的时间复杂度是O(n+m)。
接下来我们来看看算法操作过程:
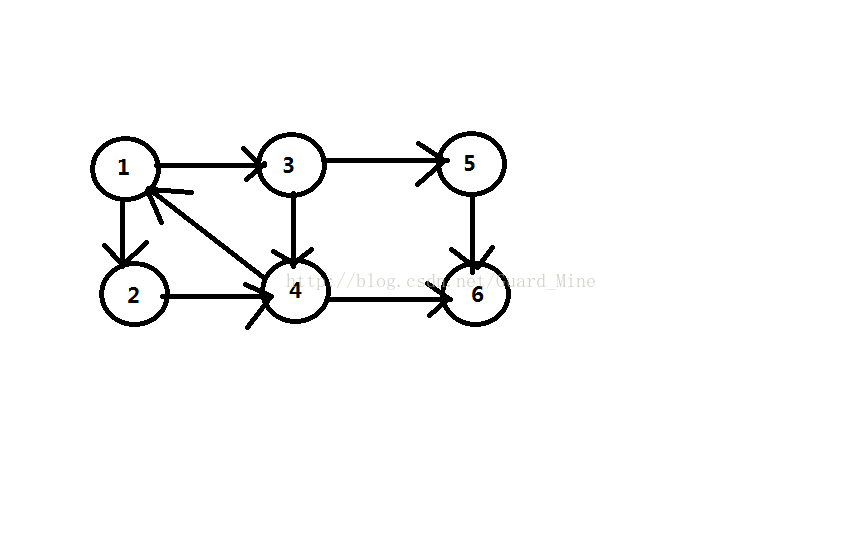
先看图
我们假设从1开始搜索
DFN[1]=1,low[1]=1;1入栈。
1->3,搜索3,DFN[3]=2,low[3]=2;3入栈。
3->5,搜索5,DFN[5]=3,low[5]=3;5入栈。
5->6,搜索6,DFN[6]=4,low[6]=4;6入栈。
6找不到边,发现DFN[6]==low[6],于是6是一个强连通分量的根,该强连通分量的元素出栈,得到强连通分量{6}
回溯到5,判断low[5]是不是要修改,事实证明不需要,同样此时5也找不到边,发现DFN[5]==low[5];
于是5是另一个强连通分量的根,该强连通分量的元素出栈,得到强连通分量{5}.
回溯到3,判断low[3]是不是要修改,事实证明不需要,
此时找到另一条边3->4,搜索4,DFN[4]=5,low[4]=5;入栈。
4->1,1已经在栈内了,判断low[4]是不是需要修改,事实证明,原先low[4]==5,而DFN[1]==1,所以现在把low[4]修改为1。4已经没有其他边。判断得到DFN[4]!=low[4],于是回溯到3,3没有其他边,回溯到1,此时得到边1->2,搜索2,DFN[2]=6,low[2]=6;2入栈。
2->4,4已经在栈内,同样可以修改low[2]=DFN[4]=1;
此外2同样找不到其他边,判断得DFN[2]!=low[2],回溯到1;
此外1同样找不到其他边,判断得DFN[1]==low[1],于是该强连通分量的元素出栈该强连通分量的元素出栈该强连通分量元素出栈。得到强连通分量{1,3,4,2};
至此这张图的3个强连通分量已经全部找到,算法执行完毕。
以上是我学了以后自己在草稿纸上模拟得到的过程,如果有错误的话,还请留言指出。
附:hdu1269代码
#include<stdio.h>
#include<string.h>
const int maxn=10005;
int DFN[maxn];//记录每个点被访问到的时间
int low[maxn];//记录点可以直接或间接到达的最早被访问到的点(也就是那个强连通分量的根)
int stack[maxn];
int sccnum[maxn];//标记每个点属于第几个强连通分量
bool instack[maxn];
int sccNum;//强连通分量的数目
int top;
int index;
int n;
struct node
{
int to;
int next;
}edge[10*maxn];
int head[maxn];
int tot;
void addedge(int from,int to)
{
edge[tot].to=to;
edge[tot].next=head[from];
head[from]=tot++;
}
void tarjan(int i)
{
DFN[i]=low[i]=++index;//刚刚搜到这个点,DFN和low都赋值为被访问到的时间
stack[top++]=i;//入栈
instack[i]=1;
for(int j=head[i];j!=-1;j=edge[j].next)
{
if(!DFN[edge[j].to])//如果没有被访问过
{
tarjan(edge[j].to);
//这个时候low可能要修改,值为i或者i的子树可以到达的最早被访问到的点的时间
if(low[i]>low[edge[j].to])
low[i]=low[edge[j].to];
}
else if(instack[edge[j].to])//已经在栈
{
if(low[i]>DFN[edge[j].to])
low[i]=DFN[edge[j].to];
}
}
if(DFN[i]==low[i])//找到根
{
sccNum++;
int v;
do
{
v=stack[--top];
sccnum[v]=sccNum;
instack[v]=0;//标记出栈
}while(v!=i);
}
}
void solve()
{
memset(DFN,0,sizeof(DFN));
memset(instack,0,sizeof(instack));
index=0;
sccNum=0;
top=0;
for(int i=1;i<=n;i++)
if(!DFN[i])
tarjan(i);
}
int main()
{
int m,a,b;
while(~scanf("%d%d",&n,&m))
{
if(n==0 && m==0)
break;
memset(head,-1,sizeof(head));
tot=0;
for(int i=0;i<m;i++)
{
scanf("%d%d",&a,&b);
addedge(a,b);
}
solve();
if(sccNum==1)
printf("Yes\n");
else
printf("No\n");
}
return 0;
}