算法入门系列二--DP入门之DAG上的DP

引言：

DAG：有向无环图。

DAG是学习动态规划的基础，很多问题都可以直接转化为DAG上的最长路、最短路或路径计数问题。

两个经典的DAG模型，嵌套矩形和硬币问题，今天先写第一个嵌套矩形问题。

一、嵌套矩形

第一个DAG模型：矩形嵌套问题
描述
有n个矩形，每个矩形可以用a,b来描述，表示长和宽。
矩形X(a,b)可以嵌套在矩形Y(c,d)中当且仅当a<c,b<d或者b<c,a<d（相当于旋转X90度）。
例如（1,5）可以嵌套在（6,2）内，但不能嵌套在（3,4）中。
你的任务是选出尽可能多的矩形排成一行，使得除最后一个外，每一个矩形都可以嵌套在下一个矩形内。

【分析】

矩形间的“可嵌套”关系是一个典型的二元关系，二元关系可以用图来建模。如果矩形X可以嵌套在Y中，则就从X到Y连一条有向边。这个图是无环的，因为一个矩形无法直接或或间接的嵌套在自己的内部。也即是说这是以一个DAG。

因此，我们就是在求DAG上的最长路径。

【问题】

这个是一个没有确定的路径起点和终点（可以把任意的矩形放在任何位置）的DAG问题。

如何求解，仿照上次的数字三角形（数塔）问题的求解，可以设d（i）表示从节点i出发的最长路的长度，如何写出状态转移方程呢？第一步只能走到他的相邻的节点，因此：

d（i）= max { d（j）+1 | i, j ∈E }

其中，E为边集。最终答案是所有的d（i）中的最大值。因此可以用递推或者记忆化搜索计算。

二、解决步骤

第一步，建图。

假如用邻接矩阵将矩形间的关系保存在矩阵G中。

第二步，编写记忆化搜索程序（调用前先初始化数组为0）。

第三步，按字典序输出最佳的方案

三、实例实践

假如有这样的五个矩形：

输入的边长分别是：

矩形宽	矩形长
3	5
4	6
2	3
7	4
6	6

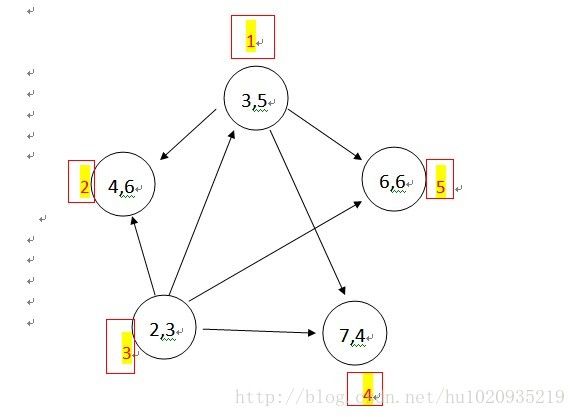
其DAG表示如下：

由图可知，最长路有3--1--2 和 3--1--4

按字典序之后只有 3--1--2

具体的代码如下：（c语言实现DAG矩形嵌套问题）

附录：代码

/***** DP初步之DAG ********/

/******** written by C_Shit_Hu ************/

////////////////动态规划入门///////////////

/****************************************************************************/
/* 
第一个DAG模型：矩形嵌套问题
描述
有n个矩形，每个矩形可以用a,b来描述，表示长和宽。
矩形X(a,b)可以嵌套在矩形Y(c,d)中当且仅当a<c,b<d或者b<c,a<d（相当于旋转X90度）。
例如（1,5）可以嵌套在（6,2）内，但不能嵌套在（3,4）中。
你的任务是选出尽可能多的矩形排成一行，使得除最后一个外，每一个矩形都可以嵌套在下一个矩形内。

输入
测试数据的第一行是一个正正数n，表示该组测试数据中含有矩形的个数(n<=1000)
随后的n行，每行有两个数a,b(0<a,b<100)，表示矩形的长和宽

输出
每组测试数据都输出一个数，表示最多符合条件的矩形数目，每组输出占一行
*/
/****************************************************************************/


// 思路：先对长和宽来此排序，再按照要求构图，
// 完成之后，直接记忆化搜索，值得注意的地方是你不能只从第一个点搜索，而是要从每个点搜索

#include<stdio.h>
#include<string.h>

#define MAXN 101
int n, G[MAXN][MAXN];     // 图的存储
int x[MAXN], y[MAXN], d[MAXN];  // 节点

//记忆化搜索来完成的动态转移
int dp(int i) 
{       
	int j;
	if(d[i] > 0) 
		return d[i];  // 如果已经计算过，直接返回其值

	d[i] = 1;         // 否则，置一，递推计算
	for(j = 1; j <= n; j++)
		if(G[i][j])   // 如果图存在，即是满足可嵌套
			if(d[i] <=dp(j)+1)     // 如果存在可嵌套的节点d(j)加一后其值大于d(i)
				d[i]=dp(j)+1;      // 则使d[i]更新

			return d[i];       // 返回d[i]
}

//按字典序只输出排序最小的序列
/*
此部分的原理：字典序只是消除并列名次的方法，我们最根本的任务还是求出最长路
在把所有的d值计算出来后，选择最大的d[i]所对应的i。而如果有多个i，则选择最小的i，这样保证字典序最小。
接下来选择d(i) = d(j) +1 且i, j ∈E 的任何一个j，但是为满足字典序最小，需选择最小的j
*/
void print_ans(int i) 
{   
	int j;
	printf("%d ", i);    // 第一次i代表最长路的起点节点，以后均代表从该节点开始的路径
	for(j = 1; j <= n; j++) 
		if(G[i][j] && d[i] == d[j]+1)  // 如果该图满足可嵌套，且d[i] = d[j] +1
		{
			print_ans(j);           // 立即输出从节点j开始的路径
			break;
		}
}

int main() 
{
	int i, j, t, ans, best;
	scanf("%d", &n);            // n表示矩形的数目
	// 初始化矩形长宽参数，并初次调整长宽顺序
	for(i = 1; i <= n; i++) 
	{
		scanf("%d%d", &x[i], &y[i]);     // 依次输入矩形的边长信息
		if(x[i] > y[i]) 
		{
			t = x[i]; x[i] = y[i]; y[i] = t;   // 保证X[]存的是长，Y[]存的是宽
		}
	}
	memset(G, 0, sizeof(G));  // 数组清零
	for(i = 1; i <= n; i++)           // 建图
		for(j = 1; j <= n; j++)
			if(x[i] < x[j] && y[i] < y[j]) G[i][j] = 1;  // 如果第i个矩形的长宽均小于第j个，使图相应的值为1
			
			ans = 0;
			for(i = 1; i <= n; i++)      // 依次递推所有的的节点
				if(dp(i) > ans) 
				{
					best = i;       // best 是最小字典序
					ans = dp(i);
				}
				printf("ans=%d\n", ans);   // 表示最长路长度
				print_ans(best);
				printf("\n");
				while(1);
			return 0 ;
}

/******************************************************/
/********************  心得体会  **********************/
/*
好好学习DP！！！
*/
/******************************************************/

运行结果如下：

未完待续。。。。

下一个---DAG之硬币问题（固定终点的最短路问题）。