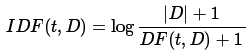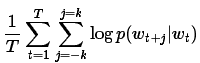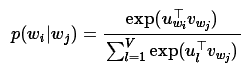Spark 1.6.1 MLlib

TF-IDF

TF-IDF是一种特征向量化方法，这种方法多用于文本挖掘，通过算法可以反应出词在语料库中某个文档中的重要性。文档中词记为t，文档记为d , 语料库记为D . 词频TF(t,d) 是词t 在文档d 中出现的次数。文档频次DF(t,D) 是语料库中包括词t的文档数。如果使用词在文档中出现的频次表示词的重要程度，那么很容易取出反例，即有些词出现频率高反而没多少信息量， 如,”a” , “the” , “of” 。如果一个词在语料库中出现频率高，说明它在特定文档集中信息量很低。逆文档频次（inverse document frequency）是词所能提供的信息量的一种度量：

此处|D| 是语料库中总的文档数，注意到，公式中使用log函数，当词出现在所有文档中时，它的IDF值变为0. 给IDF加一个防止在此情况下分母为0. TF-IDF 度量值表示如下：

TFIDF(t,d,D)=TF(t,d)⋅IDF(t,D)

对于TF 和 IDF 定义有多种，spark.mllib 中，分开定义TF 和IDF 。

　　Spark.mllib 中实现词频率统计使用特征hash的方式，原始的特征通过hash函数，映射到一个索引值。后面只需要统计这些索引值的频率，就可以知道对应词的频率。这种方式避免设计一个全局1对1的词到索引的映射，这个映射在映射大量语料库时需要花费更长的时间。但需要注意，通过hash的方式可能会映射到同一个值的情况，即不同的原始特征通过Hash映射后是同一个值。为了降低这种情况出现的概率，我们只能对特征向量升维。i.e., hash表的桶数，默认特征维度是 2^20 = 1,048,576.

注意：spark.mllib 不支持文本分段。

TF实际是统计词hash之后索引值的频次，可使用HashingTF 方法并传入RDD[Iterable[_]] ， IDF 需要使用IDF方法。需要注意，每条记录是可iterable的字符串或其它类型。

import org.apache.spark.rdd.RDD
import org.apache.spark.SparkContext
import org.apache.spark.mllib.feature.HashingTF
import org.apache.spark.mllib.linalg.Vector

val sc: SparkContext = ...

// Load documents (one per line).
val documents: RDD[Seq[String]] = sc.textFile("...").map(_.split(" ").toSeq)

val hashingTF = new HashingTF()
val tf: RDD[Vector] = hashingTF.transform(documents)

HashingTF 方法只需要一次数据交互，而IDF需要两次数据交互：第一次计算IDF向量，第二次需要和词频次相乘

import org.apache.spark.mllib.feature.IDF

// ... continue from the previous example
tf.cache()
val idf = new IDF().fit(tf)
val tfidf: RDD[Vector] = idf.transform(tf)

spark.mllib支持乎略词频低于文档最小数，需要把minDocFreq这个数传给IDF构架函数。在此情况下，对应的IDF值设置为0，

import org.apache.spark.mllib.feature.IDF

// ... continue from the previous example
tf.cache()
val idf = new IDF(minDocFreq = 2).fit(tf)
val tfidf: RDD[Vector] = idf.transform(tf)

Word2Vect (词到向量)

Word2Vec 计算词表征向量的分布，这样可以利用相似相近的词表征分布在邻近的向量空间，好处就是易于产生新型模型，且模型预测的误差也容易解释。向量分布在自然语言处理中是很有用的，特定像命名实体识别，歧义消除，句法分析，词性标记和机器翻译。

模型

　　Word2vec 的实现中，我们使用skip-gram模型。Skip-gram的训练目标是学习词表征向量分布，这个分布可以用来预测句子所在的语镜。数学上，给定一组训练词w_1, … w_T ,skip-gram模型的目标是最大化平均log-似然。

此处 k 是训练样本窗口。

　　在skip-gram模型中，每个单词w 关联两个向量u_w 和v_w ，其中u_w是单词w的向量表示，v_w是单词对应的语境。对于给定的单词w_j ，计算预测结果的正确概率由以下softmax 模型。

此处V 是词组总数

例子

　　下例子列举如何加载文本文件，将文本内容存放到RDD[Seq[String]]，从RDD构造一个Word2Vec实例，将输入数据送入此实例训练得到Word2VecModel模型。最终，我们展示特定词的前40个同义词。为了运行这个例子，首先下载text8(http://mattmahoney.net/dc/text8.zip) 数据，解压到特定的目录下。此处我们假设解压出来的文件还叫text8 ，并且在当前目录。

import org.apache.spark._
import org.apache.spark.rdd._
import org.apache.spark.SparkContext._
import org.apache.spark.mllib.feature.{Word2Vec, Word2VecModel}

val input = sc.textFile("text8").map(line => line.split(" ").toSeq)

val word2vec = new Word2Vec()

val model = word2vec.fit(input)

val synonyms = model.findSynonyms("china", 40)

for((synonym, cosineSimilarity) <- synonyms) {
  println(s"$synonym $cosineSimilarity")
}

// Save and load model
model.save(sc, "myModelPath")
val sameModel = Word2VecModel.load(sc, "myModelPath")

standardscaler标准化

标准化是通过变化将原始数据放缩到单位方差，通过平移数据得到均值为0（如果原数据均值不为0，需要对采样数据求出样本均值，将原始数据减云样本均值，即得到均值为0的新数据）。

　　例如，支持向量机的RBF 核，或L1和L2空间的正则线性模型，这两个例子很能说明问题，经过标准化所有特征的计算能得到更好的结果。

　　标准化后的数据，在最优化过程中会更快的收敛，同时也会在模型训练时防止方差大的数据对整体数据的影响。

模型拟合

　　标准化需要配置以下参数：

　　1 withMean 默认是假(false)。在标准化之前将原始数据以均值为中心，这样会使标准化后的数据分布相对紧密些，这种方法不适合于稀松的数据集，否则会触发异常。
　　2 withStd 默认是真(true) , 意味将数据标准化到单位方差。

　　在StandardScaler 中提供一个拟合方法将RDD[Vector]作为输入，学习输入的统计信息，将输入集合变换成单位标准差，变换结果可能（也可能不是）均值为0 ，通过配置StandardScaler 来实现。

　　模型支持VectorTransformer ，可以将标准向量变换成新的向量，或者将RDD[Vector] 变换到新的RDD[Vector]。

　　如果特征向量某个维度的方差为0，则特征向量这个维度的变换结果仍然是0.0

例子

　　下例展示如何加载libsvm格式数据，将数据标准化后得到新的向量，此新向量的标准差是1，均值可能（也可能不是） 0 。

import org.apache.spark.SparkContext._
import org.apache.spark.mllib.feature.StandardScaler
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils

val data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")

val scaler1 = new StandardScaler().fit(data.map(x => x.features))
val scaler2 = new StandardScaler(withMean = true, withStd = true).fit(data.map(x => x.features))
// scaler3 is an identical model to scaler2, and will produce identical transformations
val scaler3 = new StandardScalerModel(scaler2.std, scaler2.mean)

// data1 will be unit variance.
val data1 = data.map(x => (x.label, scaler1.transform(x.features)))

// Without converting the features into dense vectors, transformation with zero mean will raise
// exception on sparse vector.
// data2 will be unit variance and zero mean.
val data2 = data.map(x => (x.label, scaler2.transform(Vectors.dense(x.features.toArray))))

正规化

例子

import org.apache.spark.SparkContext._
import org.apache.spark.mllib.feature.Normalizer
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils

val data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")

val normalizer1 = new Normalizer()
val normalizer2 = new Normalizer(p = Double.PositiveInfinity)

// Each sample in data1 will be normalized using $L^2$ norm.
val data1 = data.map(x => (x.label, normalizer1.transform(x.features)))

// Each sample in data2 will be normalized using $L^\infty$ norm.
val data2 = data.map(x => (x.label, normalizer2.transform(x.features)))

ChiSqSelector(ChiSq选择器)

在模型构造阶段，特征选择从特征向量中剔除相关的维度，即对特征空间进行降维，这样可以加速迭代过程，并提升学习效率。

　　ChiSqSelector 实现基于chi-squared 的特征选择器，它处理归类特征的类标签，ChiSqSelector 基于Chi-Squared 检验对特征进行排序，而不直接考虑特征向量的类别，选取排序靠前的特征向量，因为这些特征向量能很好的决定类别标签。这就好比选取对分类有决定意义的特征向量。

　　在实际中，选取检验集可以优化特征的数量。

模型拟合

　　ChiSqSelector 算法配置 numTopFeatures 参数来确定选取排名前多少个特征向量。

　　拟合方法的输入是归类特征的RDD[LabeledPoint]，通过学习统计信息，返回ChiSqSelectorModel模型，这个模型可以用于对特征空间进行降维。这个模型可以处理输入Vector,得到降维后的Vector , 或者对RDD[Vector]进行降维。

　　当然，也可以构造一个特征索引（索引按升序排列）, 对这个索引的数组训练ChiSqSelectorModel模型。

例子

　　下例展现ChiSqSelector的基础应用，输入矩阵的每个元素的范围 0 ~ 255 。

import org.apache.spark.SparkContext._
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.util.MLUtils
import org.apache.spark.mllib.feature.ChiSqSelector

// Load some data in libsvm format
val data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")
// Discretize data in 16 equal bins since ChiSqSelector requires categorical features
// Even though features are doubles, the ChiSqSelector treats each unique value as a category
val discretizedData = data.map { lp =>
  LabeledPoint(lp.label, Vectors.dense(lp.features.toArray.map { x => (x / 16).floor } ) )
}
// Create ChiSqSelector that will select top 50 of 692 features
val selector = new ChiSqSelector(50)
// Create ChiSqSelector model (selecting features)
val transformer = selector.fit(discretizedData)
// Filter the top 50 features from each feature vector
val filteredData = discretizedData.map { lp => 
  LabeledPoint(lp.label, transformer.transform(lp.features)) 
}

Hadamard乘积(ElementwiseProduct)

ElementwiseProduct对输入向量的每个元素乘以一个权重向量的每个元素，对输入向量每个元素逐个进行放缩。这个称为对输入向量v 和变换向量scalingVec 使用Hadamard product(阿达玛积)进行变换，最终产生一个新的向量。用向量 w 表示 scalingVec ，则Hadamard product可以表示为

Hamard 乘积需要配置一个权向量 scalingVec

　　1) scalingVec 变换向量

　　ElementwiseProduct实现 VectorTransformer 方法，就可以对向量乘以权向量，得到新的向量，或者对RDD[Vector] 乘以权向量得到RDD[Vector]

例子

　　下例展示如何对向量进行ElementwiseProduct变换

import org.apache.spark.SparkContext._
import org.apache.spark.mllib.feature.ElementwiseProduct
import org.apache.spark.mllib.linalg.Vectors

// Create some vector data; also works for sparse vectors
val data = sc.parallelize(Array(Vectors.dense(1.0, 2.0, 3.0), Vectors.dense(4.0, 5.0, 6.0)))

val transformingVector = Vectors.dense(0.0, 1.0, 2.0)
val transformer = new ElementwiseProduct(transformingVector)

// Batch transform and per-row transform give the same results:
val transformedData = transformer.transform(data)
val transformedData2 = data.map(x => transformer.transform(x))

PCA

PCA可以将特征向量投影到低维空间，实现对特征向量的降维。

例子
　　下例展示如何计算特征向量空间的主成分，使用主成分对向量投影到低维空间，同时保留向量的类标签。

import org.apache.spark.mllib.regression.LinearRegressionWithSGD
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.feature.PCA

val data = sc.textFile("data/mllib/ridge-data/lpsa.data").map { line =>
  val parts = line.split(',')
  LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))
}.cache()

val splits = data.randomSplit(Array(0.6, 0.4), seed = 11L)
val training = splits(0).cache()
val test = splits(1)

val pca = new PCA(training.first().features.size/2).fit(data.map(_.features))
val training_pca = training.map(p => p.copy(features = pca.transform(p.features)))
val test_pca = test.map(p => p.copy(features = pca.transform(p.features)))

val numIterations = 100
val model = LinearRegressionWithSGD.train(training, numIterations)
val model_pca = LinearRegressionWithSGD.train(training_pca, numIterations)

val valuesAndPreds = test.map { point =>
  val score = model.predict(point.features)
  (score, point.label)
}

val valuesAndPreds_pca = test_pca.map { point =>
  val score = model_pca.predict(point.features)
  (score, point.label)
}

val MSE = valuesAndPreds.map{case(v, p) => math.pow((v - p), 2)}.mean()
val MSE_pca = valuesAndPreds_pca.map{case(v, p) => math.pow((v - p), 2)}.mean()

println("Mean Squared Error = " + MSE)
println("PCA Mean Squared Error = " + MSE_pca)