《算法导论》笔记 第16章 16.3 赫夫曼编码
【笔记】
没有一个编码是另一个编码的前缀,成为前缀编码。
最优编码总是由一棵满二叉树来表示的。
对字母表C中的每一个字符c,设f(c)表示c在文件中出现的频度,d_T(c)表示c的叶子在树中的深度。这样,编码一个文件所需的位数就是
B(T)=∑f(c)·d_T(c)
【练习】
16.3-1 证明:一棵不满的二叉树不可能与一种最优前缀编码对应。
对只有一个子结点的结点,将其子结点提升为兄弟结点必然更优。
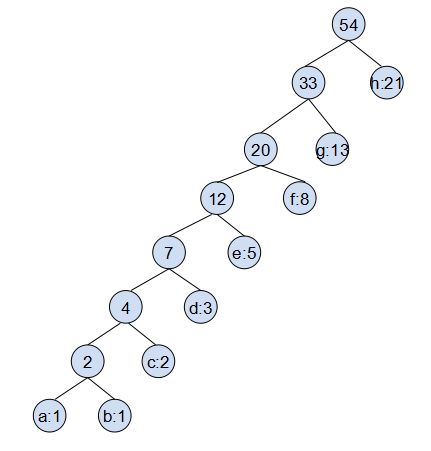
16.3-2 对下面的频度集合,其最优的赫夫曼编码是什么?a:1 b:1 c:2 d:3 e:5 f:8 g:13 h:21
变成了像这样的葡萄串。
16.3-3 证明:对应于某种编码的树的总代价也能通过计算所有内结点的两子节点的频度之和而得到。
16.3-4 证明:对一字母表的字符按其频度的单调递减顺序排序,则存在一个编码长度单调递增的最优编码。
16.3-5 假设有一个字母表C={0,1,...,n-1}上的最优前缀编码,用尽可能少的位来传输。证明:C上的任意一个最优前缀编码都可由2*n-1+n*ceil(lgn)个位的序列来表示。
16.3-6 将赫夫曼编码推广至三进制编码,并证明它能产生最优编码。
16.3-7 假设某一数据文件包含一系列的8位字符,且所有256个字符的频度都差不多:最大字符频度不到最小字符频度的两倍。证明:这种情况下赫夫曼编码的效率与普通的8位固定长度编码就差不多了。
16.3-8 证明:没有一种数据压缩方案能对随机选择的8位字符的文件作任何压缩。