小希的迷宫（并查集）

题目链接：点击打开链接

小希的迷宫

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 27263    Accepted Submission(s): 8402

Problem Description

上次Gardon的迷宫城堡小希玩了很久（见Problem B），现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样，首先她认为所有的通道都应该是双向连通的，就是说如果有一个通道连通了房间A和B，那么既可以通过它从房间A走到房间B，也可以通过它从房间B走到房间A，为了提高难度，小希希望任意两个房间有且仅有一条路径可以相通（除非走了回头路）。小希现在把她的设计图给你，让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子，前两个是符合条件的，但是最后一个却有两种方法从5到达8。 

 

Input

输入包含多组数据，每组数据是一个以0 0结尾的整数对列表，表示了一条通道连接的两个房间的编号。房间的编号至少为1，且不超过100000。每两组数据之间有一个空行。 
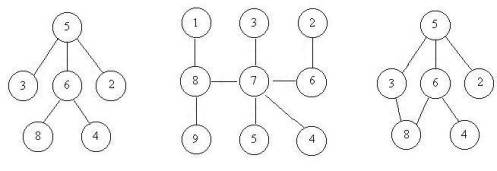
整个文件以两个-1结尾。

 

Output

对于输入的每一组数据，输出仅包括一行。如果该迷宫符合小希的思路，那么输出"Yes"，否则输出"No"。

 

Sample Input

   
   
   
   

    
    
    
    6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0

-1 -1
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Yes
Yes
No
   
   
   
   

 

Author

Gardon

 

Source

HDU 2006-4 Programming Contest

 

Recommend

lxj   |   We have carefully selected several similar problems for you:   1213  1325  1233  1198  1102 

 

分析：先把所有的点的父亲节点指向自己，然后用并查集合并，每次把合并的两个点标记为访问过的，如果中间出现要合并的 两个节点的根节点都相同，说明有环，如果最后在访问过的节点中有大于1个节点的父亲节点还是自己，说明不连通。

code：

#include<stdio.h>
#include<string.h>
int pre[100001],vis[100001],fg,max,min;
void init()
{
int i;
for(i=1;i<=100000;i++)
pre[i]=i;
memset(vis,0,sizeof(vis));
fg=1;
max=-1;
min=111111;
}
int find(int root)
{
int son,tmp;
son=root;
while(root!=pre[root])
root=pre[root];
while(son!=root)
{
tmp=pre[son];
pre[son]=root;
son=tmp;
}
return root;
}
void join(int root1,int root2)
{
int x,y;
x=find(root1);
y=find(root2);
if(x!=y)
pre[x]=y;
else
fg=0;
}
int main()
{
int a,b,cnt,i;
init();
while(scanf("%d%d",&a,&b)!=EOF)
{
if(a==-1&&b==-1)
break;
else if(a==0&&b==0)
{
printf("Yes\n");
init();
}
else
{
            if(max<a)
max=a;
if(max<b)
max=b;
if(min>a)
min=a;
if(min>b)
min=b;
join(a,b);
vis[a]=1;
vis[b]=1;
while(scanf("%d%d",&a,&b)!=EOF&&a&&b)
{
if(max<a)
max=a;
   if(max<b)
max=b;
    if(min>a)
min=a;
    if(min>b)
min=b;
    join(a,b);
vis[a]=1;
vis[b]=1;
}
cnt=0;
for(i=min;i<=max;i++)
{
if(vis[i]&&pre[i]==i)
cnt++;
if(cnt>1)
{
fg=0;
break;
}
}
if(fg)
printf("Yes\n");
else
printf("No\n");
init();
}
}
return 0;
}




大牛的另一种做法：

思想：边数==点数-1，即构成环时边数大于点数-1，不连通时边数小于点数-1，由于两点构成一条边，对于输入的每两点，边总的计数加一，最后与输入不同点的个数减一所得的值比较，即可判断。这里利用了C++STL中的set容器来实现，代码很简单，关键是做题的思想，思路决定出路！！！

#include<stdio.h>
#include<set>
using namespace std;
set<int>S;
int main()
{
int a,b;
while(scanf("%d%d",&a,&b)&&(a!=-1||b!=-1))
{
if(a==0&&b==0) printf("Yes\n"); 
int num=1; 
S.insert(a);
S.insert(b);
while(scanf("%d%d",&a,&b)&&(a||b))
{
S.insert(a);
S.insert(b); 
num++; 
} 
if(S.size()-1==num) printf("Yes\n");
else printf("No\n"); 
S.clear(); 
} 
return 0; 
}