无向图的割点，桥，双连通分量，有向图的强连通分量总结

                 一、无向图的割点，桥，双连通分量

1.割点：

 定义：

    在一张无向图中，如果去掉某个顶点以及和这个顶点相关联的边，使得整个图的连通分支数增  加，那么这个点就是一个割点.

 tarjan算法求无向图的割点：

   定义low[u],DFN[u]分别表示u可以到达的最早被访问到的祖先的时间，后者表示u被访问到的时间，那么u是割点当且仅当u满足下面2种情况之一：

    1).u是dfs搜索树的根，并且u含2棵及2棵以上的子树

    2).u不是dfs搜索树的根，并且有不等式 low[v]>=DFN[u],其中(u,v)是树枝边(即v通过u延伸开去)

 简单说明这两个情况：

    情况1：这是很显然的，如果这个时候u只有1棵子树，那么就算去掉u,整个图的连通分支数还是不会变，但是当子树个数超过1的时候，去掉u，连通分支数是会增加的.

    情况2：如果不等式low[v]>=DFN[u]成立，言外之意就是v要到达其祖先必须通过u，否则如果有其他边可以让v到达祖先的话，low[v]显然会比DFN[u]来的小，那么这时候去掉点u，图的连通分支数一定会增加.

 代码：

   

<span style="font-family:KaiTi_GB2312;font-size:18px;">void tarjan(int u,int root,int fa)  
{  
    DFN[u]=low[u]=++index;  
    instack[u]=1;  
    int cnt=0;  
    for(int i=head[u];i!=-1;i=edge[i].next)  
    {  
        int v=edge[i].to;  
        if(!instack[v])  
        {  
            tarjan(v,root,u);  
            cnt++;  
            if(low[u]>low[v])  
                low[u]=low[v];  
            if(u==root && cnt>1)  
                cut_point[u]=1;  
            else if(u!=root && low[v]>=DFN[u])  
                cut_point[u]=1;  
        }  
        else if(v!=fa && low[u] > DFN[v])  
            low[u]=DFN[v];  
    }  </span>

2.桥

    定义:

     在一张无向图中，如果去掉边(u,v)使得图的连通分支数增加，那么边(u,v)便称为桥.

  tarjan算法求无向图的桥:

     边(u,v)是无向图的桥当且仅当(u,v)满足 low[v]>DFN[u]

   简单说明:

     这个式子的言外之意也就是边(u,v)是v到达其祖先的必经之路，所以去掉边(u,v)，连通分支数就会增加，但是如果u，v之间存在重边的话，就不是桥了，所以我们要对重边判定.

   代码:

    

void tarjan(int u,int fa)  
{  
    DFN[u]=low[u]=++index;  
    instack[u]=1;  
    for (int i=head[u];i!=-1;i=edge[i].next)  
    {  
        int v=edge[i].to;  
        if (edge[i].id==fa)<span style="font-family:KaiTi_GB2312;">//edge[i].id是那条边的编号，其中由一条无向边拆成两条有向边时，这两条边编号相同</span>
            continue;  
        //printf("%d %d\n",u,v);  
        if (!instack[v])  
        {  
            tarjan(v,edge[i].id);  
            if (low[u]>low[v])  
                low[u]=low[v];  
            if (low[v]>DFN[u])  
                bridge[res++]=edge[i].weight;  
        }  
        else if (low[u]>DFN[v])  
            low[u]=DFN[v];  
    }  
}

   简单解释为什么这样可以排除重边的情况：

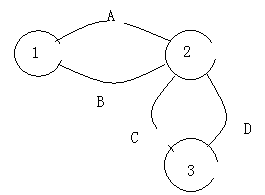
   看图：

   比如现在从1开始搜索，选择A边到2，这时2开始循环边的时候，通过

dge[i].id==fa

   将A边排除，然后如果选择B边，发现1已经被压入栈，所以B边只能拿来修改修改low[u]的值了，这样A,B两条边都无法进行

if (low[v]>DFN[u])  
                bridge[res++]=edge[i].weight;

的判断，所以排除了A,B中有桥的情况，当然2,3亦是如此.

3.双连通分量

   定义:

    在无向连通图中，如果删除该图的任何一个结点都不能改变该图的连通性，则该图为双连通的无向图。一个连通的无向图是双连通的，当且仅当它没有关键点。换言之，双连通分量里任何2个顶点之间都至少有2条不相交的路径

   tarjan算法求边双连通分量(点双连通分量较为复杂，未完待续）

    直接看代码吧：

   

<span style="font-family:KaiTi_GB2312;font-size:18px;">void tarjan(int u,int fa)
{
	instack[u]=1;
	DFN[u]=low[u]=++index;
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		int v=edge[i].to;
		if(fa==edge[i].id)
			continue;
		if(!instack[v])
		{
			tarjan(v,edge[i].id);
			low[u]=min(low[u],low[v]);
		}
		else
			low[u]=min(DFN[v],low[u]);
	}
}

</span>

然后判断每个点的low值，同一个双连通分量里的low值相同。

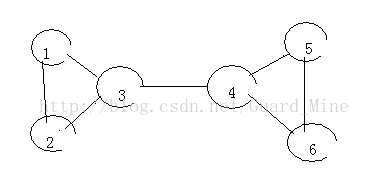
之前我还怀疑这个做法的正确性，后来自己画了个图模拟了下，就明白了。

看图：

    我们假设从1开始搜索，依次为1-3-4-5-6，之后发现6-4这条边，选择以后更新low[6]，回溯以后，low[5]也被更新，这样一来，4,5,6三个点的low值就都是4的DFN值了，也就是说，4是一个双连通分量的根;回溯到3，再到2，low[2]被更新，再回到3，low[3]被更新，这样一来，1,2,3的low值就是1的DFN值了，也就是说1另一个双连通分量的根，桥左右两边的顶点的low值不会被影响(这是我之前的疑问)

PS：如果想知道每个双连通分量里的具体点，可以设置一个栈，每次递归到一个点就压入栈，然后等这个点循环完其他所有边的时候，判断low值和DFN值是否相同，如果相同，说明这个点是一个双连通分量的根，那么就把这个点之上的点全部退出栈就行了（由于是边双连通分量，每个点只属于一个双连通分量）

二.强连通分量

   定义:

    有向图强连通分量在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

   tarjan算法求有向图的强连通分量:

    比较简单，而且我之前写过一篇关于强连通分量的，请参见：强连通分量tarjan算法