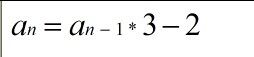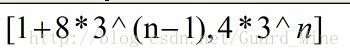NOJ1437——[1437] Shutdown
- 问题描述
-
某部队进行新兵队列训练,将新兵从一开始按顺序依次编号,并排成一行横队,训练的规则如下:从头开始一至二报数,凡报到二的出列,剩下的向小序号方向靠拢,再从头开始进行一至三报数,凡报到三的出列,剩下的向小序号方向靠拢,继续从头开始进行一至二报数。。。,以后从头开始轮流进行一至二报数、一至三报数直到剩下的人数不超过三人为止。
- 输入
-
本题有多个测试数据组,第一行为组数N,接着为N行新兵人数,新兵人数不超过5000。
- 输出
-
共有N行,分别对应输入的新兵人数,每行输出剩下的新兵最初的编号,编号之间有一个空格。
- 样例输入
-
2 20 40
- 样例输出
-
1 7 19 1 19 37
- 提示
-
无
- 来源
-
Hungar
本来不想做的,但为了自家OJ的发展以及不久就要到来的学妹们,而且这题也没人做过,于是本弱还是硬着头皮A了它。
显然就要先打表找找规律,我们可以发现,出现1段2个数的,出现1段3个数的,出现一段2个数的,出现1段3个数的.......
先来看出现2个数的,区间是[9,12],[25,36],[73,108]......
除1外出现的数是 7 19 55 ......
对于3个数的,求法也很简单,大家可以去想下,这里给出答案:
设区间为[a,b],若n<=(a+b)>>1
那么三个数就是 1,(a+1)/2,a
否则就是 1,(a+1)>>1,(a+b)/2 + 1
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int pow(int a,int b)
{
int x=1;
for(int i=1;i<=b;i++)
x*=a;
return x;
}
int main()
{
int t,n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
if(n==1)
printf("1\n");
else if(n==2)
printf("1 2\n");
else if(n==3)
printf("1 2 3\n");
else if(n==4)
printf("1 3\n");
else if(n==5 || n==6)
printf("1 3 5\n");
else if(n==7|| n==8)
printf("1 3 7\n");
else
{
bool flag=0;
int cnt;
int i;
for(i=1;i<=8;i++)
{
if(n<=4*pow(3,i) && n>=(1+8*pow(3,i-1)))
{
flag=1;
cnt=i;
break;
}
}
if(flag)//两个数
printf("1 %d\n",2*pow(3,cnt)+1);
else//三个数
{
int a,b;
for(i=1;i<=10;i++)
{
if(n>=4*pow(3,i)+1 && n<=8*pow(3,i))
{
a=4*pow(3,i)+1;
b=8*pow(3,i);
cnt=i;
break;
}
}
if(n<=(a+b)>>1)
printf("1 %d %d\n",(a+1)/2,a);
else
printf("1 %d %d\n",(a+1)>>1,(a+b)/2 + 1);
}
}
}
return 0;
}