SSE intrinsic的几个指令_mm_prefetch/_mm_movehl_ps/_mm_shuffle_ps

 

1 、 _mm_prefetch

void_mm_prefetch(char *p, int i)

The argument "*p" gives the address of the byte (and corresponding cache line) to be prefetched. The value "i" gives a constant (_MM_HINT_T0, _MM_HINT_T1, _MM_HINT_T2, or _MM_HINT_NTA) that specifies the type of prefetch operation to be performed.

T0 (temporal data)--prefetch data into all cache levels.

T1 (temporal data with respect to first level cache)--prefetch data in all cache levels except 0th cache level

T2 (temporal data with respect to second level cache) --prefetch data in all cache levels, except 0th and 1st cache levels.

NTA (non-temporal data with respect to all cache levels)--prefetch data into non-temporal cache structure. (This hint can be used to minimize pollution of caches.)

  
void _mm_prefetch(char *p, int i) 

 从地址P处预取尺寸为cache line大小的数据缓存，参数i指示预取方式（_MM_HINT_T0, _MM_HINT_T1, _MM_HINT_T2, _MM_HINT_NTA，分别表示不同的预取方式）
T0 预取数据到所有级别的缓存，包括L0。
T1 预取数据到除L0外所有级别的缓存。
T2 预取数据到除L0和L1外所有级别的缓存。
NTA  预取数据到非临时缓冲结构中，可以最小化对缓存的污染。 
       如果在CPU操作数据之前，我们就已经将数据主动加载到缓存中，那么就减少了由于缓存不命中，需要从内存取数的情况，这样就可以加速操作，获得性能上提升。使用主动缓存技术来优化内存拷贝。
 
注 意，CPU对数据操作拥有绝对自由！使用预取指令只是按我们自己的想法对CPU的数据操作进行补充，有可能CPU当前并不需要我们加载到缓存的数据，这 样，我们的预取指令可能会带来相反的结果，比如对于多任务系统，有可能我们冲掉了有用的缓存。不过，在多任务系统上，由于线程或进程的切换所花费的时间相 对于预取操作来说太长了, 所以可以忽略线程或进程切换对缓存预取的影响。

2 、 _mm_movehl_ps

Moves the upper two single-precision, floating-point values of  b  to the lower two single-precision, floating-point values of the result. The upper two single-precision, floating-point values of a are passed through to the result.

将 b 的高 64 位移至结果的低 64 位， a 的高 64 位传递给结果。

如：

r = __m128 _mm_movehl_ps( __m128 a, __m128 b ); //r = {a3, a2, b3, b2} // 高 — 低

s = _mm_movehl_ps( x , x );// 高-- 低s = {x3, x2, x3, x2}

 

例：( 代码)

  __m128 a = { 1.0f, 2.0f, 3.0f, 4.0f }; __m128 b = { 5.0f, 6.0f, 7.0f, 8.0f }; __m128 r = _mm_movehl_ps(a, b);// r = {1, 2, 5, 6}

 

3 、 _mm_shuffle_ps

Selects four specific single-precision, floating-point values from a and b,   based on the mask  i. 其中， i 是一个 8 bit 的常量，这个常量的 1~8 位分别控制了从两个操作数中选择分量的情况。

__m128 _mm_shuffle_ps(__m128 a , __m128 b , int i );

 

s = _mm_shuffle_ps( r , r , 1 )//r = {r3, r2, r1, r0}, s = {r0, r0, r0, r1}

 

它可以把两个操作数的分量以特定的顺序排列并赋予给目标数。比如

__m128 b = _mm_shuffle_ps ( a , a , 0 );

　　

则 b 的所有分量都是 a 中下标为 0 的分量。第三个参数控制分量分配，是一个 8bit 的常量，这个常量的 1~8 位分别控制了从两个操作数中选择分量的情况。而在使用 intrinsic 的时候，最好使用 _MM_SHUFFLE  宏，它可以定义分配情况。

Shuffle Function Macro

_MM_SHUFFLE(z, y, x, w)

/* expands to the following value */

(z<<6) | (y<<4) | (x<<2) | w

 

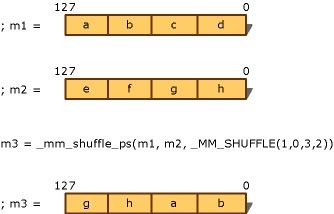
m3 = _mm_shuffle_ps(m1, m2, _MM_SHUFFLE(1, 0, 3, 2))

  It is a simple selection operation of the operands m1 and m2.

So, _MM_SHUFFLE(z,y,x,w) selects x&w 32 bit double words from m1 and z&y from m2. How simple!!.

 

one little very formal suggestion: 
_MM_SHUFFLE(z,y,x,w) does not select anything, this macro just creates a mask. SHUFPS instruction (or _mm_shuffle_ps wrapper function) performs selection, using mask created by _MM_SHUFFLE macro.

 

例：

如果定义一个共同体

typedef union {  __m128 m;  float m128_f32[4];  } my_m128;

 __m128 m1 = { 1.0f, 2.0f, 3.0f, 4.0f };

那么， m128_f32[0] = 4, m128_f32[1] = 3, m128_f32[2] = 2, m128_f32[4] = 1

 

__m128 m1 = { 1.0f, 2.0f, 3.0f, 4.0f }; __m128 m2 = { 5.0f, 6.0f, 7.0f, 8.0f }; //x.m = S1; __m128 temp = _mm_shuffle_ps(m1, m2, _MM_SHUFFLE (0, 1, 2, 3)); temp = {8, 7, 2, 1}

 

 

附： 

下面我们来复习一下叉积的求法。

c = a x b

可以写成：

Vector cross ( const Vector & a , const Vector & b ) { return Vector ( ( a [ 1] * b [ 2] - a [ 2] * b [ 1] ) , ( a [ 2] * b [ 0] - a [ 0] * b [ 2] ) , ( a [ 0] * b [ 1] - a [ 1] * b [ 0] ) ); }

那么写成 SSE intrinsic 形式则是：

/* cross */ __m128 _mm_cross_ps ( __m128a , __m128 b ) { __m128 ea , eb ; // set to a[1][2][0][3] , b[2][0][1][3] ea = _mm_shuffle_ps ( a , a , _MM_SHUFFLE ( 3 , 0 , 2 , 1 ) ); eb = _mm_shuffle_ps ( b , b , _MM_SHUFFLE ( 3 , 1 , 0 , 2 ) ); // multiply __m128 xa = _mm_mul_ps ( ea , eb ); // set to a[2][0][1][3] , b[1][2][0][3] a = _mm_shuffle_ps ( a , a , _MM_SHUFFLE ( 3 , 1 , 0 , 2 ) ); b = _mm_shuffle_ps ( b , b , _MM_SHUFFLE ( 3 , 0 , 2 , 1 ) ); // multiply __m128 xb = _mm_mul_ps ( a , b ); // subtract return _mm_sub_ps ( xa , xb ); }

 

三分量的向量求点积，可以写成：

float dot ( const float & a , const float & b ) const { return a [ 0] * b [ 0] + a [ 1] * b [ 1] + a [ 2] * b [ 2]; } 则用 SSE intrinsic 可以写成： /* x[0] * x[1] + y[0] * y[1] + z[0] * z[1] */ __m128 _mm_dot_ps ( __m128 x , __m128 y ) { __m128 s , r ; s = _mm_mul_ps ( x , y ); r = _mm_add_ss ( s , _mm_movehl_ps ( s , s ) ); r = _mm_add_ss ( r , _mm_shuffle_ps ( r , r , 1 ) ); return r ; }

 

通过这两个例子，可以留意到向量内元素的垂直相加一般形式，即：

/* x[0] + x[1] + x[2] + x[3] */ __m128 _mm_sum_ps ( __m128 x ) { __m128 r ; r = _mm_add_ps ( x , _mm_movehl_ps ( x , x ) ); r = _mm_add_ss ( r , _mm_shuffle_ps ( r , r , 1 ) ); return r ; }

那么通过扩展，可以得到求向量长度的函数，首先是求分量平方和函数：

/* x[0] * x[0] + y[0] * y[0] + z[0] * z[0] */ __m128 _mm_square_ps ( __m128 x ) { __m128 s , r ; s = _mm_mul_ps ( x , x ); r = _mm_add_ss ( s , _mm_movehl_ps ( s , s ) ); r = _mm_add_ss ( r , _mm_shuffle_ps ( r , r , 1 ) ); return r ; }

 

 

参考：MSDN

http://hi.baidu.com/sige_online/blog/item/a80522ceec812433b700c829.html

http://www.codeguru.com/forum/archive/index.php/t-337156.html

http://blog.csdn.net/igame/archive/2007/08/21/1752430.aspx