HDU1541：Stars(线段树单点更新)

Problem Description

Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.  



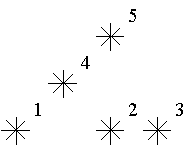
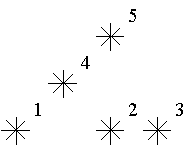
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.  

You are to write a program that will count the amounts of the stars of each level on a given map.

 

Input

The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.

 

Output

The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.

 

Sample Input

   
   
   
   

    
    
    
    5
1 1
5 1
7 1
3 3
5 5
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    1
2
1
1
0
   
   
   
   

 

 

题意：给出1~n每个星星的坐标，星星不会重叠，问0~n-1登记的星星有几个

思路：这道题还是比较巧妙的，我们可以发现我们只需要统计线段树内比x小的叶子节点的个数即可。因为题目说了按y的递增顺序给出，所以我们在一个个插入的时候们只要比较比x小的区间有多少个点即可。

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

const int maxn = 32000+10;
int tree[maxn<<2],t,x,y,ans[maxn<<2];

void insert(int l,int r,int i)
{
    if(l == r)
        t+=tree[i];
    else
    {
        int mid = (l+r)>>1;
        if(x<=mid)
            insert(l,mid,2*i);
        else
        {
            t+=tree[2*i];//走右子树，则把左子树的所有星星数目加起来
            insert(mid+1,r,2*i+1);
        }
    }
    tree[i]++;
}

int main()
{
    int n,i;
    while(~scanf("%d",&n))
    {
        memset(tree,0,sizeof(tree));
        memset(ans,0,sizeof(ans));
        for(i = 0; i<n; i++)
        {
            scanf("%d%d",&x,&y);
            t = 0;
            insert(0,maxn,1);
            ans[t]++;//等级个数
        }
        for(i = 0; i<n; i++)
            printf("%d\n",ans[i]);
    }

    return 0;
}