bzoj 2147 happiness

2127: happiness

Time Limit: 51 Sec   Memory Limit: 259 MB
Submit: 1300   Solved: 623
[ Submit][ Status][ Discuss]

Description

高一一班的座位表是个n*m的矩阵，经过一个学期的相处，每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了，每个同学对于选择文科与理科有着自己的喜悦值，而一对好朋友如果能同时选文科或者理科，那么他们又将收获一些喜悦值。作为计算机竞赛教练的scp大老板，想知道如何分配可以使得全班的喜悦值总和最大。

Input

第一行两个正整数n，m。接下来是六个矩阵第一个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。第二个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。第三个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。第四个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。第五个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。第六个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。

Output

输出一个整数，表示喜悦值总和的最大值

Sample Input

1 2
1 1
100 110
1
1000

Sample Output

1210
【样例说明】
两人都选理，则获得100+110+1000的喜悦值。
【数据规模】
对于100%以内的数据，n,m<=100 所有喜悦值均为小于等于5000的非负整数

题解：网络流求最小割

考虑到一个人，文理不可兼得，不妨先建点，然后向源点（文科），汇点（理科）连边，流量（也就是割）是对应喜悦值。（这里的想法是先建个差不多的，有漏洞再拆点啊，建辅助点啊什么的）

    然后再考虑一对朋友之间的共文理喜悦值：

如果都选文，那么需要割掉双方都选理的喜悦值，

如果都选理，那么需要割掉双方都选文的喜悦值，

如果一文一理，那么就都割。

首先对于一个点对，我们考虑到他们之间的关系只在于都选文或者都选理的喜悦值，

而求最小割时我们要割掉这部分权值，那么我们可以建边，然后把边进行处理。

一、

首先我最开始的想法是把边的权值设置为都选文+都选理的和。

这样就成功地满足了一文一理的情况。

但是却无法分开。

二、

这时候我们可以把边建成点，然后两边的人向此点连容量inf的无向边，

然后源点（文科）向此点连都选文的容量，汇点连都选理的。

这样我们就满足了都选文或者都选理的情况。

也就是都选文的话，我们就可以不割“都选文”这种权值，都选理 同理。

但是这是WA的，cheat也不行（实测），因为我们又无法让两人一文一理了。

三、

再往“一”那里考虑，发现我们有时需要把两种权值都割断。

这个时候想到：

a-(len)-->b，当len值一定，把图建成a-->b-->c-->d，只要边长都是len，那么最小割是不变的。

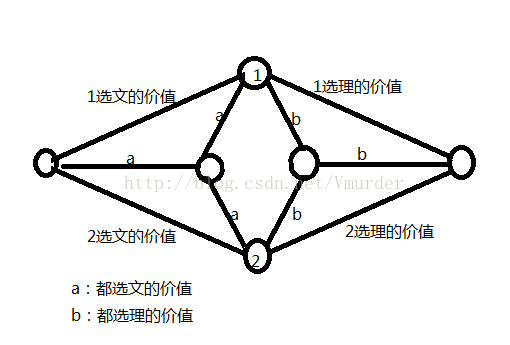
所以我们把“边点”拆成两个点，一个对应S集（文），一个对应T集（理），，

这样我们就可以把原来的inf也改成对应权值，使得割断哪一条边都是最小割值。

这么说可能有些含糊，不妨来张图。

ps:分析转载自 http://blog.csdn.net/vmurder/article/details/42609669

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int n,m,i,j,num,tot,sum,numl;
int next[600000],v[600000],cost[6000000],point[50003];
int deep[50003],cur[50003];
const int inf=1e9;
void add(int x,int y,int z)
{
  tot++; next[tot]=point[x]; point[x]=tot; v[tot]=y; cost[tot]=z;
  tot++; next[tot]=point[y]; point[y]=tot; v[tot]=x; cost[tot]=0;
}
bool bfs(int s,int t)
{
 memset(deep,0x7f,sizeof(deep));
 for (int i=0;i<=numl;i++)
  cur[i]=point[i];
 deep[0]=0;
 queue<int> p;
 p.push(0);
 while (!p.empty())	
  {
  	int now=p.front(); p.pop();
  	for (int i=point[now];i!=-1;i=next[i])
  	 {
  	 	if(deep[v[i]]>inf&&cost[i])
  	 	 {
  	 	 	deep[v[i]]=deep[now]+1;
  	 	 	p.push(v[i]);
  	 	 }
  	 }
  }
 if (deep[t]>inf) return false;
 else  return true;
}
int dfs(int now,int t,int limit)
{
	if (now==t||!limit)  return limit;
	int flow=0,f;
	for (int i=cur[now];i!=-1;i=next[i])
	 {
	 	cur[now]=i;
	 	if (deep[v[i]]==deep[now]+1&&(f=dfs(v[i],t,min(limit,cost[i]))))
	 	 {
	 	 	flow+=f; limit-=f;
	 	 	cost[i]-=f; cost[i^1]+=f;
	 	 	if (!limit) break;
	 	 }
	 }
	return flow;
}
int dinic(int s,int t)
{
  int ans=0;
  while(bfs(s,t))
   ans+=dfs(s,t,inf);
  return ans;
}
int main()
{
  scanf("%d%d",&n,&m);
  tot=-1;
  memset(point,-1,sizeof(point));
  memset(next,-1,sizeof(next));
  num=n*m;
  numl=n*m+2*(n-1)*m+2*(m-1)*n+1;
  for (i=1;i<=n;i++)
   for (j=1;j<=m;j++)
    {
      int x; scanf("%d",&x); sum+=x;
      add(0,(i-1)*m+j,x);
    }
  for (i=1;i<=n;i++)
   for (j=1;j<=m;j++)
    {
      int x; scanf("%d",&x); sum+=x;
      add((i-1)*m+j,numl,x);
    }
  for (i=1;i<=n-1;i++)
   for (j=1;j<=m;j++)
    {
      int x; scanf("%d",&x); sum+=x;
      num++;
      add(num,(i-1)*m+j,x);
      add(0,num,x);
      add(num,i*m+j,x);
    }
  for (i=1;i<=n-1;i++)
   for (j=1;j<=m;j++)
    {
       int x; scanf("%d",&x); sum+=x;
       num++;
       add((i-1)*m+j,num,x);
       add(i*m+j,num,x);
       add(num,numl,x);
    }
  for (i=1;i<=n;i++)
   for (j=1;j<=m-1;j++)
    {
      int x; scanf("%d",&x); sum+=x;
      num++;
      add(num,(i-1)*m+j,x);
      add(num,(i-1)*m+j+1,x);
      add(0,num,x);
    }
  for (i=1;i<=n;i++)
   for (j=1;j<=m-1;j++)
    {
      int x; scanf("%d",&x); sum+=x;
      num++;
      add((i-1)*m+j,num,x);
      add((i-1)*m+j+1,num,x);
      add(num,numl,x);
    }
  printf("%d",sum-dinic(0,numl));
}