基于ADI Blackfin系列DSP处理器的C语言编程与优化——优化DSP Kernel
第一部分介绍了ADI Blackfin DSP上的C编程的基本概念;本部分主要介绍用于DSP kernel的基本的优化方式;而第三部分则主要讲述如何直接利用DSP的feature,如用C如何采用硬件循环和circular循环寻址、如何使用pragmas和inline的汇编。
Next --》 利用DSP特性进行循环的优化
一直以来,数字信号处理应用的性能往往取决于所谓的手工优化的核,这些循环由消耗大量运算时间的特定的数学运算组成。其他部分的代码可以统称为control part。控制部分代码只消耗很少的MIPs,一般情况下直接用C实现即可。循环核跟控制代码的区分直接影响处理器的设计,如DSPs有针对循环核优化的硬件结构,包括专用指令和寄存器。现在的单处理器已经不再区分循环核跟控制代码了。新的应用程序也不以操作类型来区分循环核以及控制部分代码了。 而编译器的优化也是针对整套代码,而这时C写的DSP核就成为需要考虑的优化重点了。
浮点运算
DSP算法通常用浮点运算实现,大多数软件设计软件中使用C(或者Matlab)的实现为了保证运算精度通常主要采用双精度浮点,但大部分DSP平台都是定点处理器。在过去,这意味着C代码必须从浮点操作转变成定点运算,而这种转变很痛苦,需要保证精度而进行不断的定标和scale调整。但现代的DSPs处理器主频变得越来越高,实际的代码实现仅需要把critical部分进行浮点的转换而不需要关注其他部分,这就大大降低了开发的复杂度,这通常还会利用DSPs在编译器中包含的浮点库,通常这些浮点库只是为了保证算法的可移植性,因而在没有原生浮点的处理器中性能很差,这些库还会忽略IEEE浮点标准的某些特性,因而也并不能保证浮点算法的平台完全一致。图1是与IEEE不兼容和兼容的浮点库在ADI的Blackfin处理器上的性能比较。左侧的优化代码性能相对兼容模式的浮点库性能提升很大。
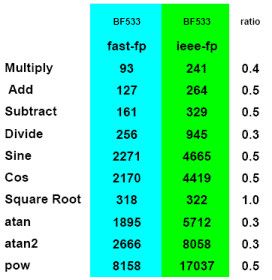
图 1. IEEE-compliant (right) vs. non-compliant (left) floating-point libraries.
另外你需要考虑你是否真的需要ANSI C可移植标准定义的64-bit的双精度浮点运算,很多应用场合如automotive和audio场合,32-bit单精度浮点精度已经足够,使用单精度能加速程序运行无论是在支持浮点的处理器还是只能软件模拟浮点的处理平台。
分数运算
为了保证精度同时又能有较高的速度,你可以选择一个高速的浮点库,最好这个浮点库要能够快上100倍以满足你的性能要求,要不你可以选择分数运算,这种实现在定点处理器平台通常比浮点运算快上100倍。但是分数数据类型不是一个可移植C的标准类型,在ANSI标准的编译器并不清楚该数据是分数还是整型的。通常情况下只能程序员自己来创建分数类型。另一个方法是提高编译器的语义能力的以希望能够理解复杂的大块的C与分数操作。这是具有挑战性的,但是这是能够做到的。还可以提供intrinsics(或内建函数)来直接告诉编译器。这种方法虽然看起来很笨拙,但通常是一种提高性能的有效的编程风格。
基于以上实现的弊端,一种很好的实现也许是参考c++中定义新的类型和重载操作符。这可能似乎是一种自然的方式来表达分数运算,但C和C++的语义差距很大,c++语言的能力比C,但是这意味着它更为自动。例如,c++编译器竟然可以自己创建构造函数和析构函数。同时,C ++风格包含更多的间接的方式,这可能会导致编译器需要进行别名分析。例如c++程序会产生更多的临时变量,另外C++往往用目标object和结构体而不是变量来表达,不利于编译器的优化。
改进的语义分析的例子
图 2是一个分数运算的一个C实现。
y[i] += ((scaler * x[i] ) >>15 );
如果编译器足够强大的话,以上的一句实现可以用DSP上的一条分数乘累加指令实现(即分数MAC)。
上面的这种方法可以使你保留C的可移植性,但它留下了许多问题。如果我们会遇到溢出,或需要代码的饱和算法时呢?当我们进一步研究DSP的乘累加单元时,是用乘累加MAC都会有额外的位宽来处理溢出情况,还是在每次循环内都对数据进行scale呢? (有符号变量较为容易处理溢出,因为C语义对于无符号的溢出要更为严格) 。上面的处理在循环体比较小时更为简单有效,但是如果分数运算的个数非常多,再继续让编译器做语义分析就非常困难了。
Intrinsics内联汇编
另一个方法是使用intrinsics,这是给编译器预先定义的基本运算以确切的了解程序员的意图。Intrinsics看起来像函数调用,但他们往往是map成单一指令。由于是用intrinsics让编译器了解程序员的意图和内在的影响,这样就能进行有效的优化。在编译器手册里提供了intrinsics(也称为内置函数)的定义。图3显示使用intrinsics实例。

图 3. Intrinsics看起来像函数调用,但他们往往是map成单一指令add_fr1x32和 mult_fr1x32 intrinsics.
内联Intrinsics的一个缺点是名字晦涩、很难记住。此外Intrinsics的代码往往被经常批评不文雅。不过,一套intrinsics出现在多个平台就会创造一个事实上的标准。图4显示的这些都是ITU / ETSI built-ins显示在。这些intrinsics是欧洲电信标准协会为了明确GSM的解码器而定义的。使用这些built-ins在各种平台支持下是一个快速的方法来构建分数算法。
是用intrinsics写代码是,需要检查其精确的定义,这样才能让您保持平台可移植性。
循环核的编译器优化
一般编译器将假设您的大部分的时间都花在内循环上。因此如果内循环迭代次数较少或者代码较少,编译器做出的优化效果往往不佳。大多数内循环优化靠循环展开loop unroll。是用循环展开,编译器扩展了代码,以便让它可以产生更多的机会为指令重排、避免stall,并组合指令来实现并行执行操作。达到这些目标的两个基本技术是软件流水和矢量化pipeline和vectorization。
软件流水能让循环内的若干分离的单一指令组合成在一个机器周期内执行的效率更高的代码。如图5所示,在循环的第三次迭代时,就可以先储存第一个迭代结果(S1),同时做第二个迭代(M2)的MAC运算以及为第三次迭代(L3)加载数据输入。这样就实现在一个周期多个操作的并行处理。一个周期只处理一个操作或者一条指令是非常低效率的。
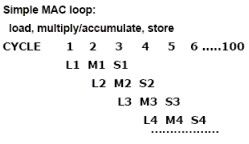
图 5. 包含加载 (L),乘累加 (M), 存储 (S)操作的软件流水,其中的标号表示第几次迭代如 L1表示第一次迭代的加载.
矢量化(也称为SIMD)意味着在一个以上的数据元素进行运算。这种技术的好处是显而易见的:如果每次循环你处理多个数据,你需要花更少的周期来处理所有数据。图6说明了SIMD这个概念在机器代码层面的表现,首先是机器指令的生成,即加载数据,我们将每一个16位数据单独加载并执行一个multiply-accumulate操作。而在第二版的代码中编译器则应用矢量话,组合两个矢量的迭代循环,每次存取取32位或者两个16-bit的数据。最后我们看到的向量化加上软件流水的影响。总体效果是6倍的速度提升。值得注意的是代码大小已经变化,同时由于SIMD的引入,需要加入循环退出的判别条件。
为了加快你的代码执行,你可以检查你的代码,看看是否有你不希望看到的结果出现,如果存在,你应该问问自己为什么。是提供给编译器的信息的遗漏还是代码结构避免编译器优化呢?以下因素是在代码check时需要考虑的:
-
Alias混叠的数据。如果两个数据缓冲buffer是重叠的,编译器将不会以矢量为单位优化循环;
-
Data dependencies数据相关,如果一个计算结果依赖于前一次循环,编译器将不会利用SIMD的矢量优化循环。后面我们会看一些例子;
-
连续内存的访问:如果我们从存储器去加载两个或多个操作数,尽可能把这些操作数安排在连续的内存空间;
-
适当的数据对齐:许多处理器平台只是取数据项的地址的倍数的数据大小。即如果我们想加载32位数据,我们应该确保数据的32位的地址上对齐;
-
简化循环体:保持循环比较短,并且从循环内去除条件语句和控制语句以利用硬件循环;
-
使控制流透明:使用常数或常量,而不是在循环内的控制变量或全局变量。换句话说使用
for (n=0; n>100; n++)
而不是
for (n=start; n<stop; n+=step)
如果编译器可以看到多少次迭代循环,它就能在循环次数较少时避免昂贵的向量化操作。另外如果循环的递增值在编译时不可知,编译器也不会选择SIMD,而未知的循环起始和结束值也会让编译器加入多余的循环prolog和epilog的代码。
-
在一些处理器中,进行数据访问时,要顺序向前而不是向后可能会更有优势:
-
好的和坏的表达方式
前面已经提到,数据相关会让编译器避免SIMD。图7显示的是两种常见的数据相关,有时候数据相关是无法避免的,尤其是那些需要紧密反馈的算法,如IIR滤波器。但是程序员需要尽可能的避免引入这些相关,除非确实需要。 -
作为对比,图8演示的是有利于编译器优化的操作。递加代替递减,有利于MAC使用;数据算术加法和乘法关联操作,这意味着编译器可以自由排序数据的索引,从而认为是没有相关的;
-
尽可能的简化
为了引导你的编译器,也许最重要的事情就是保持你的代码简单。这很容易让编译器去了解你的意图 -
不要手动将内部循环展开。你也许会认为一个循环展开会帮助编译器,但这可能会迷惑编译器。图9是一个例子,另外手动展开外循环是需要的,编译器不会展开外循环。
-
同样,不要手动进行软件流水的优化,除非你在写汇编代码。图10显示为什么这是一个问题。左边是一个简单的循环,你可以想象一个编译器可以容易的理解。在右边,程序员试图软件流水该代码,但编译器却难以理解程序员的真实意图。
Reference
http://www.eetimes.com/design/signal-processing-dsp/4017024/Programming-and-optimizing-C-code-part-2
-
第一部分介绍了ADI Blackfin DSP上的C编程的基本概念;本部分主要介绍用于DSP kernel的基本的优化方式;而第三部分则主要讲述如何直接利用DSP的feature,如用C如何采用硬件循环和circular循环寻址、如何使用pragmas和inline的汇编.






