HDOJ 4686 Arc of Dream 矩阵快速幂
矩阵快速幂:
根据关系够建矩阵 , 快速幂解决.
Arc of Dream
Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)Total Submission(s): 2164 Accepted Submission(s): 680
Problem Description
An Arc of Dream is a curve defined by following function:
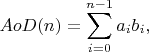
where
a 0 = A0
a i = a i-1*AX+AY
b 0 = B0
b i = b i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?
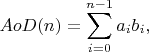
where
a 0 = A0
a i = a i-1*AX+AY
b 0 = B0
b i = b i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?
Input
There are multiple test cases. Process to the End of File.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10 18, and all the other integers are no more than 2×10 9.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10 18, and all the other integers are no more than 2×10 9.
Output
For each test case, output AoD(N) modulo 1,000,000,007.
Sample Input
1 1 2 3 4 5 6 2 1 2 3 4 5 6 3 1 2 3 4 5 6
Sample Output
4 134 1902
Author
Zejun Wu (watashi)
Source
2013 Multi-University Training Contest 9
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long int LL;
const LL mod=1000000007LL;
struct Matrix
{
int x,y;
LL m[6][6];
Matrix() {x=y=5;memset(m,0,sizeof(m));}
void one()
{
for(int i=0;i<5;i++) m[i][i]=1LL;
}
void show()
{
cout<<x<<" * "<<y<<endl;
for(int i=0;i<x;i++)
{
for(int j=0;j<y;j++)
cout<<m[i][j]<<",";
cout<<endl;
}
}
};
Matrix Mul(Matrix& a,Matrix& b)
{
Matrix ret;
ret.x=a.x; ret.y=b.y;
for(int i=0;i<a.x;i++)
{
for(int j=0;j<b.y;j++)
{
LL temp=0;
for(int k=0;k<b.y;k++)
{
temp=(temp+(a.m[i][k]*b.m[k][j])%mod)%mod;
}
ret.m[i][j]=temp%mod;
}
}
return ret;
}
Matrix quickPow(Matrix m,LL x)
{
Matrix e;
e.one();
while(x)
{
if(x&1LL) e=Mul(e,m);
m=Mul(m,m);
x/=2LL;
}
return e;
}
LL n,A0,B0,AX,AY,BX,BY;
Matrix init_matrix()
{
Matrix ret;
ret.m[0][0]=1;
ret.m[1][0]=AY; ret.m[1][1]=AX;
ret.m[2][0]=BY; ret.m[2][2]=BX;
ret.m[3][0]=(BY*AY)%mod; ret.m[3][1]=(AX*BY)%mod;
ret.m[3][2]=(BX*AY)%mod; ret.m[3][3]=(AX*BX)%mod;
ret.m[4][3]=1LL; ret.m[4][4]=1LL;
return ret;
}
Matrix Beg()
{
Matrix beg;
beg.m[0][0]=1;
beg.m[1][0]=A0;
beg.m[2][0]=B0;
beg.m[3][0]=A0*B0%mod;
return beg;
}
int main()
{
while(cin>>n)
{
cin>>A0>>AX>>AY>>B0>>BX>>BY;
A0=A0%mod; AX=AX%mod; AY=AY%mod;
B0=B0%mod; BX=BX%mod; BY=BY%mod;
Matrix m=init_matrix();
m=quickPow(m,n);
Matrix beg=Beg();
LL ans=0;
for(int i=0;i<5;i++)
ans=(ans+beg.m[i][0]*m.m[4][i]%mod)%mod;
cout<<ans<<endl;
}
return 0;
}