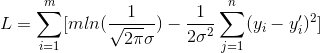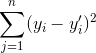[置顶] Projection Matrix and Linear Regression

假如想把一个向量投影到一个空间，我们想得到投影后的向量，那么我只需要用一个投影矩阵乘以原来的向量就能得到投影后的矩阵，那么如何得到这个投影矩阵呢，下面开始推导，首先从一维空间开始：

对于上面这幅图来说，a,b都是向量,x是一个数，可以得到：

解出:

           

因为aTb是一个数字，所以我们能将数字和向量a交换，得到投影后的向量xa。对于投影到一维空间来说，

就是投影矩阵。

投影到多维空间时，有：

x1*a1+x2*a2+...+xn*an则是投影后的向量,写成矩阵形式就是：

可以解出：

其中

就是投影矩阵，A=(a1,a2,...,an)，a1,a2,an为该空间的基。X=(x1,x2,..xn)T,x1,x2..xn分别为基的线性组合的系数，可以发现多维的投影矩阵形式和一维有点相似，一维也可以写成多维的这种形式。

投影有个非常重要的性质就是：假如我想在A的列空间找一个离b最近的向量(最近指的是，向量每一维差值平方和最小)，那么最近的向量就是b投影到A空间的投影向量。

我之所以说重要，因为他关系到线性回归最小二乘法的解，假如现在我们要做直线(多维情况下应该说超平面)拟合，方程为：AX=y,一般情况下，这个方程是无解的，不然也不需要拟合了，拟合效果好坏的评价就是最小二乘，就是求解Ax=y',其中，y'在A的列空间里(即AX=y'有解)，并且要保证，y与y'的距离最小。根据前面投影的性质，这个y’就是y在A的列空间的投影。那么我们我们求解Ax=y',解出的x向量就是最佳直线(超平面)。有：

            

解出这个有解的方程，就得到最佳拟合直线(超平面)了。

对于最小二乘的来源，我觉得还是有必要说明下，为什么我们要用最小二乘来衡量优劣，而不用四次方，八次方，或者绝对值的和呢，据我所知，这是根据假设yi满足均值为y'i,方差为σ的高斯分布所得出来的结果，即y服从

分布(其中，y=(y1,y2,...ym)T,y'=(y'1,y'2,...y'm)T,i=1..m,m为点的个数,然后可以写出似然函数：

发现中括号里面的前面部分不依赖y'i，不影响求最大值，可以省去，最后我们其实求

这个式子的最小值，这与最小二乘是同一个目的。

最后我想说的是，有时候虽然叫线性回归的拟合，其实可以是多项式拟合或者其他拟合，比如现在有m个点，每个点数据都是n维的，那么最简单的拟合方法就是，将每一维直接映射过来(注意可以多加一维,每个点都设为1，作为常数项),但是我也可以把第二维的平方，第三维的立方....映射过来，这样的结果就是多项式拟合了。

另外，这样线性回归的方法会导致过拟合的问题，关于过拟合的意思，prml里面有详细的讲解,我的理解大概就是，我为了尽量拟合给定数据集，而丧失了数据本身的规律，而利用贝叶斯思想，能一定程度上克服这个问题。