立体匹配导论
转载请注明出处:http://blog.csdn.net/wangyaninglm/article/details/51531333,
来自:
shiter编写程序的艺术
2.1 视差理论
计算机立体视觉系统通过模仿人类的的视觉系统,根据对同一场景从不同位置拍摄的两视角或多视角图像,采用几何方法可以计算出深度信息。本文主要研究的双目立体视觉系统如下图所示
双相机系统
在相似三角形和中根据对应边的比例关系:

其中Z为场景的深度,b为相机基线之间的距离,f为相机焦距。且由于bf/Z
为正数,根据上式有xl>xr,由此极大简化了匹配算法。一般算法中,垂直方向上的视差采用标准的立体相机系统,即针对已经在水平方向上矫正了的图像。垂直方向上的视差为0。
2.2 立体匹配约束
由于立体匹配是从二维图像中恢复三维信息,其本身具有不确定性的特征,因此为了获取正确的匹配结果,需要借助各种约束信息来降低匹配的搜索难度,提高匹配的准确度。常用的约束信息有以下几种。
2.2.1 极线约束
由一个三维点和它在两相机成像平面的点构成的平面包含基线,即连接两个相机中心和连接两个极线直线构成的平面,该平面被称为极平面。图中P点及其投射点Or和Ol构成极平面,极平面与相机成像平面交线为极线。空间点P在成像平面上的投影点pl以及pr位于相应的极线上。
极线约束将搜索图像点的问题在立体匹配领域由二维搜索问题降低为一维搜索问题,极大简化了问题复杂度。在标准的立体视觉系统中,极线与图像的扫面线共线。
2.2.2 相容性约束
相容性约束也称为一致性约束,它要求在待匹配的两幅图像中,对应区域的特征值差别在给定阀值之内或者对应的特征点应具有相同的属性。在判断待匹配图像中的两个基元是否具有相容性约束时,可以选择的特征有以下三类:
1.像素特征,如灰度值等
2.光照特征
3.几何特征(质心,形状,边界,轮廓)
2.2.3 唯一性约束
唯一性约束要求对于待匹配图像,在原图像中至多对应一个点。该约束简化了匹配过程。一幅图像上的每个基元只能与另一幅图像上的唯一一个基元相对应,这样图像中的每个匹配基元最多只能有一个视差值
2.2.4连续性约束
2.3 立体匹配方法
在立体匹配中,匹配问题可以被看成寻找两组数据相关程度的过程[3]。立体匹配方法有多种分类,本领域内对于匹配算法的经典划分方法为两组层次结构:局部匹配算法和全局匹配算法。其划分依据是基于算法运行时约束的作用范围。另外一种划分是基于生成的视差图。对于所有像素都能生成确定视差值的称为稠密视差图,该类方法成为稠密匹配该种方法应用广泛,例如图像合成等。另一方面,与稠密视差图对应的是稀疏视差图,称为稀疏匹配,其只对被选择的像素点(通常为角点或者边缘点)有视差值,此类方法计算速度快,但需要后期通过插值算法处理缺失的视差值,所以应用场景有很大限制。本文主要针对经典的划分介绍立体匹配算法。
2.3.1 局部匹配算法
基于局部区域约束的匹配算法利用给定位置周围的局部信息进行计算,涉及信息量较少,计算复杂度较低,大多实时性平台借鉴了此算法的思想。但其对无纹理、视差不连续和遮挡区域匹配效果不理想。局部算法一般可以分为两类:特征匹配算法,区域匹配算法。
*(1)特征匹配
该类方法首先从待匹配图像中提取特征,用相似性度量和一些约束条件确定几何变换,最后将该变换作用于待匹配图像。这类方法主要包括特征提取、特征匹配、模型变换、插值与视差求精等几个步骤。
特征匹配算法是根据待匹配图像中的特征:灰度变化,边缘,光照等,建立其对应关系,并根据插值算法得到视差图的过程。特征匹配对图像噪声,遮挡不敏感,运算量小且计算时间短,但只能获取稀疏的视差图,在插值运算时容易丧失精度,对低纹理区域的匹配效果不好。
*(2)区域匹配
该类方法使用匹配窗,对所有子区域匹配窗口进行相似性度量来确定对应的区域。区域匹配中有两个问题很重要,一是相似性准则的选取,一是窗口的选取。一些常用的区域匹配相关准则有:
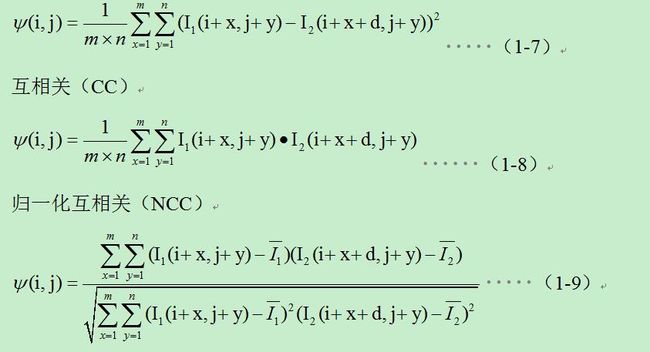
其中互相关度量和归一化互相关度量的值越大说明相似度越高,其余的值越小说明相似度越高。在窗口选择方面,影响匹配效果的关键性因素是匹配窗口的大小,窗口过小就不能包含足够的亮度信息,使亮度变化与图像噪声的比值很小,使得误匹配率升高;窗口过大,则对视差边缘不能很好的体现,且计算量升高,同时匹配效果也有所降低。
2.3.2 全局优化匹配算法
图像问题的求解可以看成是马尔科夫随机场框架下的最大后验概率求解,并进一步转换为能量最小化问题的求解。全局匹配方法首先构造一个能量函数,其形式一般为![]() ,其中数据项描述了匹配程度,平滑项体现了定义场景的约束,动态规划(DP)、置信扩展(BP)、图割(GC)、模拟退火(SA)、扫描线优化(SO)、协作算法(CA)等优化算法都可以作为求解能量最小化的方法。其中动态规划、置信扩展和图割是最常用的方法。
,其中数据项描述了匹配程度,平滑项体现了定义场景的约束,动态规划(DP)、置信扩展(BP)、图割(GC)、模拟退火(SA)、扫描线优化(SO)、协作算法(CA)等优化算法都可以作为求解能量最小化的方法。其中动态规划、置信扩展和图割是最常用的方法。
*(1)动态规划
该类方法利用每条扫描线上的顺序性约束将匹配的能量函数看作是从扫描线的起点到终点的最小代价路程问题。最优路径的代价是所有子路径代价之和,这些子路径所经过的点的匹配代价可以由区域相关度量算子来决定。
动态规划算法将问题分解为多个阶段决策进行。多个阶段互相联系并做出决策,从而使整个过程能量最优。通过在规划平面上搜索最佳路径得到最优的匹配。动态规划在一维优化中能够达到全局最优,但又因为它是在扫描线上进行匹配,使得它在扫描行之间存在严重的拖尾现象。
由于动态规划得到的是每条极线的最佳匹配而没有考虑极线与极线之间的约束关系,人们加入了极线间约束来得到极线间能量函数的最小值。与其他优化方法相比,动态规划的优点在于它为那些缺乏纹理而容易产生误匹配的区域提供了全局约束,解决了这些区域由于不同视差下的局部能量值都很低而难以匹配的问题。对于遮挡问题,动态规划中一般都将遮挡部分的能量用一个固定的值来代替,然后利用一致性约束来检测遮挡。动态规划方法的缺点是错误匹配可能沿核线方向扩展而导致其他正确匹配的失败,因此利用动态规划方法得到的视差图上经常有条纹出现。
*(2)置信扩展
置信扩展算法最早在1988年由Pearl提出,1999年以后它被广泛应用于计算机视觉的各个领域来解决具有环的图结构的优化问题并得到了不错的结果。该算法对于没有环的图结构可以收敛到最优解,但对于有环的图结构不能保证收敛到最优解。目前该算法的研究重点是如何提高算法的效率。 Sun等[25]在2003年将置信扩展算法应用到立体匹配中并取得了很好的结果,2005年,Sun等又在算法中加入了可见性约束来检测遮挡现象。Felzenszwalb等[26]提出了层次置信扩展算法,从多个方面提高了置信扩展算法的速度。yang等[38]利用层次置信扩展算法实现了遮挡了检测。Tappen和Freemanl[28]分别用图割和置信扩展对同样参数的Potts模型马尔可夫随机场进行优化,结论是置信扩展比图割的结果更平滑,速度也比图割快,但能量高于图割,两者的效果是相当的。
*(3)图割[8][9][23][24]
近年来,随着图的优化算法在计算机视觉中的应用,基于图割的能量函数的最小化问题受到了很大的关注。Roy[18]最早将图割算法应用于立体匹配,并通过实验表明,图割算法能有效克服其他全局优化算法的缺点(如动态规划算法等生成视差图产生的横向条纹瑕疵),避免了视差在临近极线处不连续的问题。但该算法生成的视差图轮廓边缘模糊,视差层的区分度低。Boykov与Kolmogorov[15]利用特定约束构造能量函数,并通过改进的最大流方法进行能量函数的最小化,将该图割算法应用于立体匹配问题,取得了效果良好的致密视差图。(并且证明了图割方法在能量最小化时候取得的最小值和全局最小值相差一个已知常数)但该方法构建网络图时生成了大量节点,导致空间复杂度较高,同时,该算法运算过程需要多次迭代,时间复杂度高,无法达到实时计算的要求。为了提高匹配速度Li[19]提出基于无重叠视差区域分割的立体匹配,并用分割块的能量最小化取代了常用图割算法像素级的能量最小化,降低了算法的时间复杂度,但生成的视差图边缘处有毛刺现象。Bleyer[20]等人利用图像在每个分割块中的视差具有光滑性的特点,提出了基于图像分割的立体匹配算法的通用算法。但该方法无法得到像素级的最优分配,且复杂度高,计算量大。Bleyer与Rother[21]针对现有采用基于低尺度分割,将图像分割成超像素形式从而减少图割算法生成节点的立体匹配方法。假设相同物体具有紧凑、连接并且物体表面视差变化平滑等特性,提出了一种新的基于物体分割的立体匹配方法。该方法虽然在物体分割与视差获取上效果良好,但是运算量大,对于物体和背景的内部区域缺少纹理的深度信息,并且物体间的区域没有准确的视差标注。
上述文献中基于图像分割的立体匹配方法,由于采用自动化非交互的彩色图像分割方法会把相同视差的区域分开或隐去了图像的部分细节信息,导致分割误差,而消除误差需要引入其他方法,如通过引入初试视差估计[20][21]等方法,但这些方法增加了立体匹配算法的整体复杂度,而且没有有效利用分割信息。在实际应用场景中为了获取感兴趣区域的精细视差图,针对于以往基于图像分割的立体匹配算法复杂、计算量大,没有充分利用分割结果的信息等缺点,提出了一种基于交互式图像分割的立体匹配方法。该方法在图像分割时采用可交互的图割方法获得感兴趣目标,只针对感兴趣目标进行立体匹配,因此运算量大大减少,同时保留了原有图割算法具有的全局最优特性。
2.4 遮挡
立体匹配中存在的不可见问题是由于场景的几何结构和场景中物体的遮挡。所谓遮挡是指由于场景中的景物与摄像机之间的相互位置关系所导致的场景中的某些点在一个摄像机中可见,而在另外一个摄像机中不可见的情况。由于景物深度不同,距离摄像机较远的景物就可能被距离摄像机较近的景物遮挡,从而不能形成图像而且,由于视点的变化,景物的遮挡区域可能发生变化,某一视点下可见的场景区域在另一个视点下可能成为遮挡区域,这种现象称为半遮挡现象。计算机视觉中研究的遮挡现象几乎都属于半遮挡现象。遮挡问题的非双目可见性以及伴随的表面不连续性,使它不满足立体视觉的一些约束的要求,是立体视觉研究中的一个难点和重点所在近年来,人们对遮挡区域的检测和测量,乃至恢复遮挡区域的正确深度估计等方向进行了大量的研究,提出了若干遮挡问题的解决方案。
在实际的匹配系统中,为了克服遮挡问题,需要针对遮挡点进行深度插值运算。
2.5遮挡检测方法
交叉检查=左右检查LRC(在有低空间频率结构的场景中结果较差)
点顺序约束(ORD)
如果在两幅图像中,匹配点的顺序不同,那么在场景中的匹配点就是遮挡点。(整体有最低的误判率和最低的触发率)
遮挡约束(OCC)
假设视差图中的不连续区为遮挡区,所以,要找到遮挡区域,只需要找到视差图中的不连续区域。这个过程执行两次:一次是用左图像作为参考,另一次用右图像作为参考。
2.6立体匹配的评价方法
错误匹配率的定义如下[3]:
其中,为整个图像的像素数,为计算出的视差图,为真实的视差图,在比对中,标准的真实视差图只取跟分割模板相同的部分,其余全部设置为背景,为误差容许值,一般情况下对于正整数范围内的视差标注取1。
[1]白明, 庄严, 王伟. 双目立体匹配算法的研究与进展[J]. 控制与决策, 2008, 23(7):721-729. DOI:doi:10.3321/j.issn:1001-0920.2008.07.001.
[2]赛干内克. 三维计算机视觉技术和算法导论[M]// 国防工业出版社, 2014.
[3]Cyganek B, Siebert J. An Introduction to 3D Computer Vision Techniques and Algorithms[J]., 2009.
[4]尹传历, 刘冬梅, 宋建中. 改进的基于图像分割的立体匹配算法[J]. 计算机辅助设计与图形学学报, 2008, 第6期(6):808-812.
[5]王保丰, 周建亮, 唐歌实,等. 嫦娥三号巡视器视觉定位方法[J]. 中国科学:信息科学, 2014, 04期(04):452-460.
[6]尹传历, 刘冬梅, 宋建中. 改进的基于图像分割的立体匹配算法[J]. 计算机辅助设计与图形学学报, 2008, 20(6):808-812.
[7]朱代先. 基于双目视觉的工件定位与抓取研究[J]. 计算机测量与控制, 2015, 19(1):92-94.
[8]顾骋, 钱惟贤, 陈钱,等. 基于双目立体视觉的快速人头检测方法[J]. 中国激光, 2014, 01期(01):150-155.
[9]朱素杰, 周波, 刘忠艳. 一种基于相位的立体匹配算法[J]. 工业仪表与自动化装置, 2013, 第2期(02):101-104.
[10]Yang Q. A non-local cost aggregation method for stereo matching[C]// Proceedings / CVPR, IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2012:1402-1409.
[11]Yang Q, Ji P, Li D, et al. Fast stereo matching using adaptive guided filtering[J]. Image and Vision Computing, 2014, 32(3): 202-211.
[12]Yang Q. Hardware-efficient bilateral filtering for stereo matching[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2014, 36(5): 1026-1032.
[13]Yang Q. Stereo Matching Using Tree Filtering[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2015, 37(4):834-846.
[14]Geiger A, Roser M, Urtasun R. Efficient large-scale stereo matching[M]//Computer Vision–ACCV 2010. Springer Berlin Heidelberg, 2011: 25-38.
[15]Boykov Y, Kolmogorov V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(9): 1124-1137.
[16]Bleyer M, Gelautz M. Graph-cut-based stereo matching using image segmentation with symmetrical treatment of occlusions[J]. Signal Processing: Image Communication, 2007, 22(2): 127-143.
[17]Bleyer M, Rother C, Kohli P, et al. Object stereo-joint stereo matching and object segmentation[A]// IEEE Conference on Computer Vision and Pattern Recognition[C], 2011 June 21-23, Colorado, USA :3081-3088.
[18]Roy S, Cox I J. A maximum-flow formulation of the n-camera stereo correspondence problem[A]// IEEE International Conference on Computer Vision[A], 1998 January 4-7, Bombay India:492-499.
[19]Hong L, Chen G. Segment-based stereo matching using graph cuts[A]// IEEE Conference on Computer Vision and Pattern Recognition[C],2004 June 27-July 2,Washington DC USA:74-81.
[20]Bleyer M, Gelautz M. Graph-cut-based stereo matching using image segmentation with symmetrical treatment of occlusions[J]. Signal Processing: Image Communication, 2007, 22(2): 127-143.
[21]Bleyer M, Rother C, Kohli P, et al. Object stereo-joint stereo matching and object segmentation[A]// IEEE Conference on Computer Vision and Pattern Recognition[C], 2011 June 21-23, Colorado, USA :3081-3088.
[22]Tang M, Gorelick L, Veksler O, et al. GrabCut in One Cut[A]// IEEE International Conference on Computer Vision[C], 2013 Dec 01 - 08, Sydney, Australia 1769-1776.
[23]王年, 范益政, 鲍文霞等. 基于图割的图像匹配算法[J]. 电子学报, 2006, 34(2):232-236.
转载请注明出处:http://blog.csdn.net/wangyaninglm/article/details/51531333,
来自:
shiter编写程序的艺术
