台湾国立大学机器学习基石.听课笔记（第十四讲）：Regularization

台湾国立大学机器学习基石.听课笔记（第十四讲）：Regularization

1，Regularization Hypothesis set

我们有上一讲的假设集合可知：

我们发现发生overfitting的一个重要原因可能是假设过于复杂了，我们希望在假设上做出让步，用稍简单的模型来学习，避免overfitting。例如，原来的假设空间是10次曲线，很容易对数据过拟合；我们希望它变得简单些，比如w 向量只保持三个分量（其他分量为零）。

图中的H^(')_2优化问题是NP-Hard 的。如果对w 进行更soft/smooth 的约束，可以使其更容易优化，所以我们改为：

我们将此时的假设空间记为H(C)，这是“正则化的假设空间”。而w_(REG)为正则化空间的正则化项。

2，Weight Decay Regularization

通过前面的分析，我们已经把优化问题变为向量形式，其形式为：

接着我们从几何意义上去解释拉格朗日问题，得到以下结论：

我们对上面最后一个式子从两个方面分析：

1、把E_in(g)带入

2、从此式子的原函数考虑

通过上述两种解释，我们得到了下一步我们要的augmented error； 那么从上述式子可以看出，在不同lambda下，所得到的E_(aug)(w)不同：

我们从上面lambda不同的值可以得出：

总的来说，lambda 越大，对应的常数C 越小，模型越倾向于选择更小的w 向量。
这种正规化成为 weight-decay regularization，它对于线性模型以及进行了非线性转换的线性假设都是有效的。

有时我们为了更加直观的了解各个分量的意义，还会用上勒记得多项式·：

3，正规化与VC 理论(Regularization and VC Theory)

VC bound 与 regularizator 的联系：

1、从各自的定义式考虑

E_(aug)与[E_(out)-E_(in)]的定义是：

所以：

根据VC Bound理论，Ein 与 Eout 的差距是模型的复杂度。也就是说，假设越复杂（dvc 越大），Eout 与 Ein 相差就越大，违背了我们学习的意愿。
对于某个复杂的假设空间H，dvc 可能很大；通过正规化，原假设空间变为正规化的假设空间H(C)。与H 相比，H(C) 是受正规化的“约束”的，因此实际上H(C) 没有H 那么大，也就是说H(C) 的VC维比原H 的VC维要小。因此，Eout 与 Ein 的差距变小。所以我们可以用E_(aug)代替E_(in)。

2、从物理意义上来说

我们得到的d_(eff)(H,A)比d_(vc)(g)要小得多，所及计算复杂度也进一步降低。

4，泛化的正规项 (General Regularizers)

指导我们更好地设计正规项的原则：target-dependent, plausible, friendly.

L2 and L1 Regularizer:

此处为下一讲做铺垫。

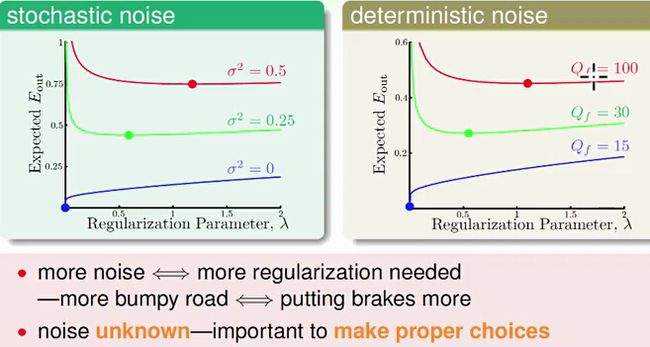
lambda 当然不是越大越好！选择合适的lambda 也很重要，它收到随机噪音和确定性噪音的影响。

总结