的确是伪随机~
C语言的 <stdlib.h> 里 rand() 函数可以产生 0 ~ RAND_MAX (包括)之间的随机数,通常是经过 srand() 函数进行初始化后再使用。
RAND_MAX 的值默认是 32767 即 2^15-1 ,在 <stdlib.h> 里的定义是 #define RAND_MAX 0x7fff;
所以如果需要求 [a, b] (显然要有 b <= RAND_MAX)之间的随机数就可以这样:
value = rand() % (b - a + 1) + a;
然而这样做会出现一个小问题,虽然影响不大,但还是值得谈谈。
举个例子,假如需要产生 [1, 6] 之间的随机数,用上面的方法计算就是
ans = rand() % 6 + 1;
即把一个随机数对 6 取模,产生一个 0~5 的值,将这个值加上 1 并返回。但是,如果随机数生成函数所返回的最大值是 32767,那么这些值就不是“概率相等”。从 0~32765 返回的值所产生的 0~5 之间各个值的概率相等,都是 5461/32768。但是,最后两个值,32766 和 32767 的返回值将分别是 0 和 1,这使它们的出现概率有所增加(是 5462/32768)。由于我们需要的答案的范围很窄,所以这个差别是非常小的。
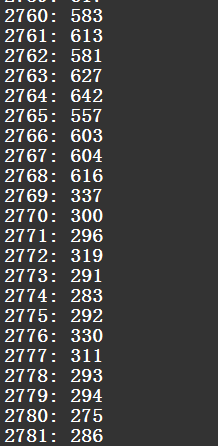
如果这个函数试图产生一个范围在 [1, 30000] 之间的随机数时,那么前 2768 个值的出现概率将是后面那些值的两倍!做个实验,我们要产生 10000000 个 [1, 30000] 之间的随机数;按照之前的说法,1~2768 之间的数出现的概率是 2/32768,而 2769~30000 之间的数出现的概率是 1/32768;因此 1~2768 之间的数出现的次数约为 10000000 * (2 / 32768) = 610 次,而 2768~30000 之间的数出现的次数约为 10000000 * (1 / 32768) = 305 次。
源代码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#define MAXN 30000 /* 随机数范围 */
#define N 10000000 /* 试验次数 */
int count[MAXN+2];
/* 设置随机种子 */
void Seed()
{
static int is_seed = 0;
if(!is_seed){
srand((unsigned int)time(NULL));
is_seed = 1;
}
}
/* 计算 beg~end 的随机数*/
int Cal_rand1(int beg, int end)
{
return rand() % (end - beg + 1) + beg;
}
int main()
{
int i;
freopen("out.txt", "w", stdout);
Seed();
for(i = 1; i <= N; i++){
int num = Cal_rand1(1, MAXN);
count[num]++;
}
for(i = 1; i <= MAXN; i++)
printf("%d: %d\n", i, count[i]);
return 0;
}
结果为:(显示一部分)
的确如此!那如果需要每个数出现的概率必须相同怎么办?有一个简单的方法:
比如要产生的最大随机数是 b,则令 t = ((RAND_MAX + 1) % b) * b - 1,那只要 rand() 函数一旦出现大于 t 的数就重新产生随机数(其实就是把多出来的那部分去掉~),直到产生的数不大于 t。
修改后的程序:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#define MAXN 30000 /* 随机数范围 */
#define N 10000000 /* 试验次数 */
#define MAX_OK_RAND \
(int)((((long)RAND_MAX +1) / MAXN) * MAXN - 1) /* 允许产生的随机数最大值 */
int count[MAXN+2];
/* 设置随机种子 */
void Seed()
{
static int is_seed = 0;
if(!is_seed){
srand((unsigned int)time(NULL));
is_seed = 1;
}
}
/* 计算 beg~end 的随机数*/
int Cal_rand2(int beg, int end)
{
int value;
do{
value = rand();
}while(value > MAX_OK_RAND);
return value % (end - beg + 1) + beg;
}
int main()
{
int i;
freopen("out.txt", "w", stdout);
Seed();
for(i = 1; i <= N; i++){
int num = Cal_rand2(1, MAXN);
count[num]++;
}
for(i = 1; i <= MAXN; i++)
printf("%d: %d\n", i, count[i]);
return 0;
}
还是比较接近的,这虽然是个小问题,但也是说大不大,说小不小的问题,既然发现就记录下(来自《C 和指针》第 16 章课后习题)。。。