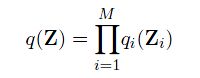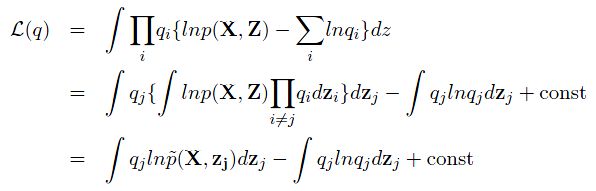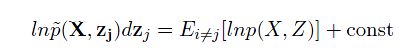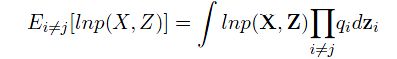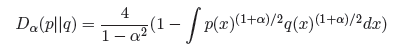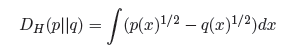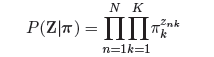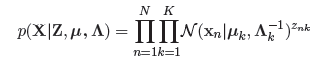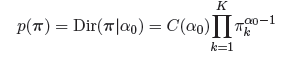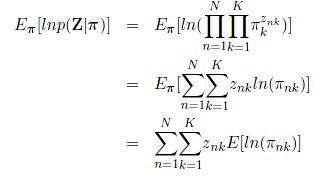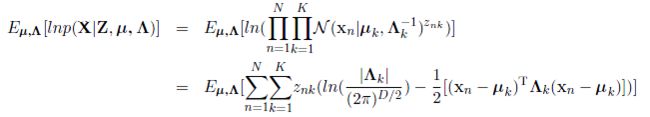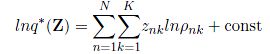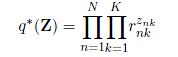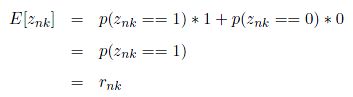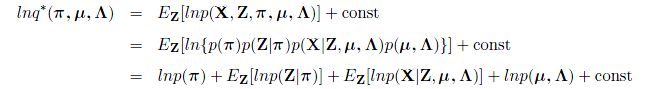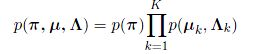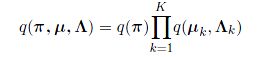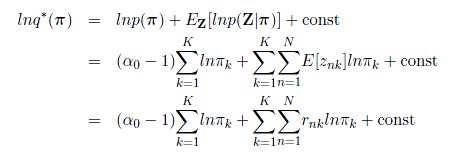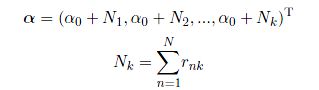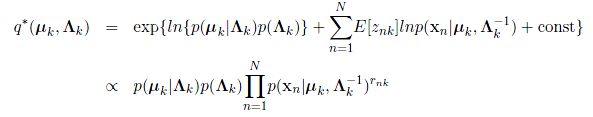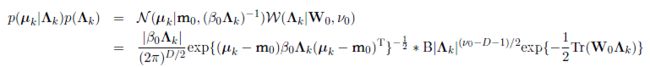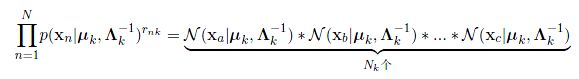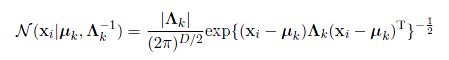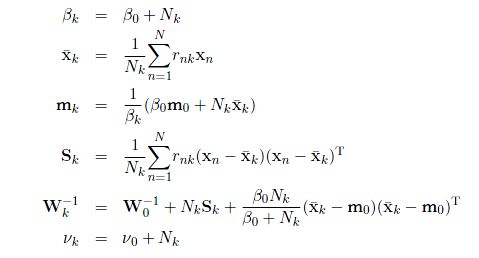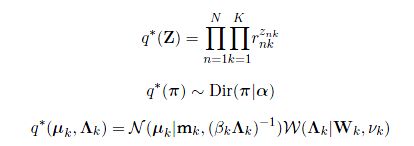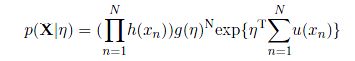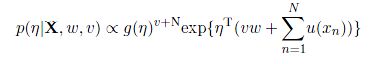An Introduction to Variational Methods

转自：    http://hi.baidu.com/zentopus/item/a91a1ef042b7cd2c743c4c88

这一系列的文章，用以对Variational Methods（变分法），做一个粗浅的入门介绍，主要的描述和依据来源于Bishop的书《pattern recognition and machine learning》   和 Jordan的书《graphical models exponential families and variational inference》，有兴趣的同学可以自行深入研究。

     我预先假设读者有一定的数学知识，包括微积分，概率等基本的知识。并且，讨论的基础是概率图模型，我也假设读者在这一方面具有一定的基础知识。

     在计算机科学中，图论（Graph theory）在很多计算领域有很重要的意义。除了用以建模之外，图论在理解计算复杂度等方面也有很重要的意义。特别的，一些算法的计算复杂度或者是其误差的范围，可以利用图的结构来进行阐述。

     图论的这些性质，在图模型中也适用。例如，我们所知道的基本的图模型算法，Junction Tree Algorithm （这不是一个算法，而是一类算法），可以看做用变量构成的图之中的一些迭代过程。对于稀疏的图，该类算法提供了一种有效的计算似然值等统计量的好的算法。

     然而，我们也知道，并不是很多的问题都是足够稀疏。所以Junction Tree Algorithm 无法再提供更多的帮助。这时候我们可以求助一类方法，称作 Markov Chain Monte Carlo (MCMC) Framework， 这是一组抽样方法，比较常见的有吉布斯抽样等等方法。这类方法，在其理论上，如果有足够的计算资源和足够多的样本，是可以无限接近真实结果的，而其无法达到真实结果的原因，是因为没有无限的计算资源。这是一种在结构上准确，在计算上进行近似的方法。

     除此之外，我们还可以去利用另外一种近似方法，称作variational methods（变分法）。这也是我在这一系列文章中将重点讨论的方法。这种方法可以结合指数家族一起使用，能够得到很好的效果。这种方法的本质上，是一种结构上的近似，利用原本不可分析的结构，将其在结构上，利用一些可分解的结构进行代替和近似，而后进行求解。

     变分法本身，也是多种近似求解方法的总称，而不是某种特定的算法。其本质上，可以看做是一种优化问题。我们将需要求解的问题表述为一个优化问题，而后在一定条件下，利用变分法将这个问题“relax”，从而进行求解。

     最后稍微提及一下，MCMC和变分法，都是有很强的物理基础，其在统计物理中的应用，更早于在CS中的应用。对于这两种方法，UC Berkeley的Jordan，以及UoE的Bishop都有很好的著作进行了比较详尽的描述。

    我们知道，很多问题都可以转化成为一个优化问题，在一个优化问题里，我们一般的做法，是利用某些方法，在整个space进行搜索，从而找到我们所希望的解，这种思想在很多领域都很常见。而我们所利用的变分法，可以看做是在这个基础上进行的一种对于优化问题求解的方式。

    其基本的想法是，我们不在整个空间中去寻求结果，而是在一个限定的范围内进行求解。例如，我们只考虑针对二阶形式的多项式函数进行求解，或者是我们将解的形式限定为一系列基函数（basis functions）的线性组合，而我们所控制的变量就是其组合的系数。而对于概率推论中，我们可以将这种限定的形式表现为，对需要优化的分布选择一种特定形式的分解，利用这样一种假设，我们来获取优化问题的近似解。这和我在系列（1）中所提到的是相互吻合的，我们要做的，是一种结构上的近似，而其后的推论是直接的。而MCMC是一种结构上的完全拟合，而是在求解过程中，因为无法获得无限计算资源而产生的一种近似。

    我们现在来深入考虑这个问题，假设我们有一个完全的Bayesian Model，即所有的参数都有一个先验分布。假设所有的潜在变量都用Z表示，可观测变量用X表示。现在给定一个数据集，并且所有的数据点都是i.i.d的。我们的模型能够描述联合分布p(X,Z)，而我们的目标是为了找出后验分布P(Z|X)，以及Model Evidence P(X)。 进一步的，我们将边缘似然值进行分解，得到：

‍
    其中，我们定义了：

‍
‍

‍
‍

    需要提及的一点是，并不是整个模型当中，对于各种分布没有其本身的参数，例如我们在Linear Gaussian System假设Z本身符合一个Gaussian分布，其需要有参数均值和方差。这些参数，因为我们有一个假设是整个模型为完全的Bayesian Model，所以这些参数都是随机变量，而可以规划到Z之中去了。

    因为KL-Divergence始终是非负的，所以，我们为边缘似然值找到了一个下界。而我们优化的方法就是提升下界从而达到优化的目的。这也等价于最小化KL-Divergence。如果我们允许q(Z)有无限种的选择的话，即我们可以在整个空间当中为其确定函数形式，那么下界最大化的时候，就等价于KL-Divergence为0的时候。这时候，我们有q(Z) = p(Z|X)。

    问题在于，如果后验是Intractable的，我们该如何控制q(Z)，来使得KL-Divergence最小化。所以，我们在此限制了q(Z)的选择范围，我们仅允许其在一组受限的tractable distributions中进行选择。并且，对于这一组分布，我们需要其足够灵活，从而能够更好地近似后验分布。并且，灵活的模型能够从一定程度上避免过拟合的问题。有一种很直观的限制这种分布的想法，利用一组参数w来控制所有的潜在变量，即引入p(Z|w)，从而，下界会成为w的一个函数，而后我们可以利用标准的非线性方法来进行优化，获取w。

    这种方法十分直观，但是这个方法并不是我们在这里需要讨论的。我们用另外一种方法，来约束q(Z)的范围。假设，我们可以将Z进行分组，分成M组，并且，我们认为，q(Z)可以依赖这个分组进行分解，得到：

‍
‍

    这就是Variational Methods的一个基础，关于细节，我在下一节中进行讨论。

在之前讨论到，在变分法中，我们假设分布存在一种可以分解的形式作为其近似，并且约束分布分解的形式，其必须是tractable和灵活的。我们所做的假设是，将潜在变量Z进行分组，分成M组，并且，我们认为，q(Z)可以依赖这个分组进行分解，得到：

‍

需要强调的是，我们不需要对分布做更多的假设了，特别的，我们对每一个分解得到的因子‍不做任何函数形式上的限制。这种分解的框架，在物理学中有其广泛的应用，对应的框架称作mean field theory。

现在，我们寻求一种分布，从而使得L(q)最大化。因而，我们希望针对q(Z)的分解得到的子分布的每一个部分，都进行优化，从而得到全局的优化。我们将分解的形式代入原本的L(q)中，可以得到：

‍‍‍‍‍

这其中，我们定义了一个新的分布：

‍

其中的期望为：

‍

现在，如果我们保持所有的‍不变，只是单纯地调整qj，我们就可以在可控的情况下，逐步最大化L(q)。而从L(q)最终的分解式中，我们又可以发现，我们得到了一个新的KL-Divergence，是‍和‍之间的KL距离。从而我们获得了关于优化解的一个一般形式：

‍

从这个式子中，我们看出，对于单个因子的优化解，是有所有潜在变量和可观测变量的联合分布的似然值，对于所有其他潜在变量求期望而得。不过，我们从这个式子当中还不能看出完整的求解过程。实际在，在真实的应用中，我们会寻求一种迭代的求解方式，首先初始化所有的因子分布，而后固定其余的，依次优化每一个，直至收敛为止。值得提及的一点是，因为每一个因子分布都是convex函数，故可以保证其收敛性。

我们之前已经简单讨论了Variational Methods，我在这里将会简单地讨论一下它的性质。

我们在系列(3)的最后，给出了对于q(Z)的解的一般优化形式：

我们注意到，求解任何一个部分，都需要利用到另外的其余所有变量保持不变，我们在实际应用中，每次只变动一个变量，依次不断更新。可以将这一个过程想象成为，在一个旋转的阶梯上不断向上移动的过程：每次都只能上一个台阶，而一个圆周上的台阶数量是固定的。当完成一周之后，你回到原本的台阶的上方，而后继续重复这样一个过程，直至到达顶部为止。虽然不准确，但是这样的想象过程和我们的近似求解过程有一定的相似之处。

我们在之前的过程中，求解的是KL(q||p)，我们不禁会问，如果我们选择KL(p||q)这样一个距离，会出现什么样的结果呢。事实上，这会导致一个非常接近的框架，在Machine Learning的术语中，我们会得到一种在图模型中求解近似解的方法，称作expectation propagation.

如果我们选择最小化KL(p||q)，则在一般的情况下，我们依然可以将q(Z)进行分解，得到：

代入新的KL-Divergence，我们会得到：

其中的常数不依赖于p(z)，我们可以引入拉格朗日乘数来优化这个式子，从而得到以下的解：

在这样的情况下，我们发现q(Z)每个分解因子的优化解，就为其对应的p(Z)的部分，并且这是一个闭型解，不需要进行迭代求解。

如果我们将这两种不同的方法应用于同一个问题，我们会得到什么样的结果呢，我们可以看图 1。

从图中我们可以明显的发现，这两种方法都准确地找到了需要近似的函数的均值，但是两者在对方差进行描述的时候，都出现了一定的误差。也就是说，两种方法在把握概率密度的时候，都不能够做得非常准确。那么，出现这两者差异的原因是什么呢？为了解释这个问题，我们再看一下KL(q||p)到底是什么：

注意这个式子，如果p(Z)不趋近于0，q(Z)是不会趋近于0的，也就是说，q(Z)会自动地避免p(Z)密度低的地方。这样的话，就会得到图\ref{EpVsVm}中(a)的那样，我们发现近似结果对于原分布中为0的地方是无法发现的。而如果我们利用相反的KL-Divergence，则我们会得到相反的结果。为了使得KL(p||q)最小化，q(Z)会在p(Z)不为0的地方也取0，从而使得式子最小。

在实际的应用中，我们并不是总是应对单峰的分布，对于多峰的分布，如果我们最小化KL(q||p)，则根据初始值的不同，一般会找到其中一个最优值。而如果我们选择最小化KL(p||q)的话，一般会将分布进行平均的分配，这样的结果是非常不利于进行预测的。所以，为了要应用之一方案，我们需要作出调整，那将会得到expectation propagation的算法。这已经超出了这一系列文章的范围，我就不多做讨论了。我们可以从图2中得到一些直观的感受。

其实，这两种距离都是alpha-family距离中的一员，其定义为：

特别的，当alpha为0的时候，我们会得到一种对称的距离，称作Hellinger Distance:

本文中的两幅图，都来源于Bishop的大作Pattern Recognition and Machine Learning

‍‍在这篇文章中，我引用Bishop书中的一个例子，来简单介绍一下Variational Methods的应用。想要更详细地理解这个例子，可以参考Bishop的书Pattern Recongnition and Machine Learning的第十章。

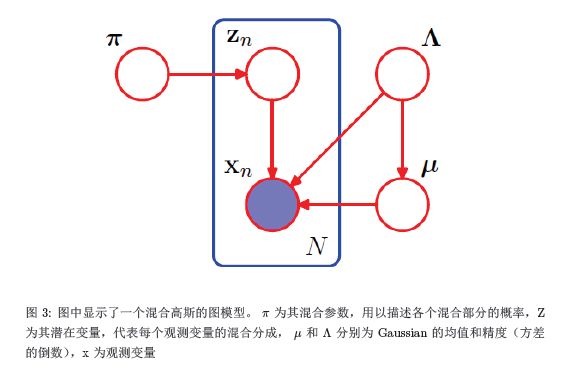
这个例子应用于一个混合高斯分布，我们先来看一看这个混合高斯分布的图模型，见图3，从而可以进一步退出其概率表达式。

‍

现在我们有了这个图，我们就不难写下一个完整的概率式来表示整个联合分布：

‍

现在，我们来定义一些分布。首先，我们已经说过，这是一个混合高斯模型，那么就需要有一个变量来描述，一个点的生成，到底是由这个混合高斯中的哪一个组成部分生成。那么这个变量就是Z，我们用一个1-of-K的二进制向量来表示。例如我现在有一个二进制向量(0,0,0,0,1)，这个向量代表一共有五个组成部分，而这个点对应于其中的第五个组成部分。这就是一个multinational distribution。那么我们现在要来控制这个multinational distribution，那就需要利用到pi。现在我们假设有N个观测变量构成的数据集，每一个观测变量都对应其潜在变量。我们可以得到：

‍

在这里， 我们假定，在这个高斯混合中，一共有K个组成部分。现在，我们需要写出观测变量基于潜在变量的条件分布。

‍

现在，我们可以引入分布来描述这些参数，从而构成一个完整的Bayesian Model。首先，我们来描述pi。我们注意到Z是一个由pi控制的multinational distribution，那么根据其共轭先验，我们可以方便地选择Dirichlet distribution作为pi的先验分布，从而我们有：

‍

在这个式子中，我们将Dirichlet分布做了一个简化，其控制参数，我们减少为一个。关于Dirichlet分布的介绍可以看我另外一篇文章Simple Introduction to Dirichlet Process。现在我们需要为Gaussian的均值和方差引入一个控制先验。从我们之前的图模型中，我们发现了均值对精度的依赖（这并不是必须的）。在均值和精度都不知晓的情况下，我们可以为这两个参数引入一个Gaussian-Wishart先验分布，这是在对于高斯分布的两个控制参数均不了解的情况下其共轭先验。从而我们有：

‍

现在，整个问题就完全定义了，接下来就是如何利用Variational Methods来解决这个问题。

首先，回忆一下在Variational Methods里，我们是如何实现近似的。对，我们是利用一种结构上的近似，也就是假设我们现在想要求的分布，可以分解为一系列tractable的分布，从而进行近似于求解。在给定的现在这样一个完全Bayesian Model中，我们选择一种分解方式，来将原有的结构进行分解近似。从而我们得到：

‍

这是一种合理的假设，我们将潜在变量和控制参数分开，从而得到这样的一种分解。这里有几点值得说明：首先，我在前面的文章中提到，我们是将Z分解为几组，从而得到近似模型。那为什么这里除了Z之外，还有别的变量？这是因为，当时我用Z代替的了所有的变量，当时的Z之中包含了控制参数，因为这是一个完全的Bayesian Model。第二个要注意的是，这个分解的假设，是我们在这个例子中作出的唯一假设了。

现在，我们利用之前得到的公式，将现在的这个式子代入，我们可以得到：

‍

而后，我们利用最初根据图模型得到的那个全概率分解形式，可以对上面的式子进行简化，并且将于Z无关的式子都放入常数中，从而得到：

‍

接下来，我们就可以将上面式子中提到的两个分布分别代入，分别可以得到：

‍

以及

‍

我们注意到，这两个式子有相同的部分，为了使得表达更加简洁，我们引入一个新的符号：

‍

从而我们有：

‍

在这个式子的基础上，我们等式两边同时取对数，则我们得到：

‍

这个分布还是没有归一化的，所以我们需要进行归一化，则我们定义：

‍

从而对该分布进行归一化，得到最终的关于Z的分布：

‍
‍

其余参数的近似，我将会在下一篇文章中继续讨论。

我们现在已经得到了关于潜在变量Z的优化分布的表达形式：

‍

其中：

‍

所以现在我们可以得到Z的期望：

‍

另外对于Z还值得一提的是，我们从其优化分布的表达式中可以看出，各个Z的组成部分之间还是相互耦合的，所以需要一个迭代的求解方式。

解决了关于Z的一些遗留的问题，我们可以继续讨论如何求解余下的参数。同样的，我们的基本想法，还是将其带入我们之前所求到的公式中去，从而，我们有：

‍

现在，我们回头去观察一下这个混合高斯分布的图模型，我们会发现，在控制变量中，本身存在一个独立性，即：

‍

从而，在近似模型中，我们有：

‍

于是，我们从这些参数的优化表达式中，分别提取出只关于部分参数的式子，进行进一步优化，即：

‍‍

现在，我们对上式两边同时求指数运算，则：

‍
‍

看到这个形式是不是觉得非常熟悉呢？没错，这是一个Dirichlet分布的标准形式，从而我们可以得到关于pi的优化分布：

‍

其中

‍

我们现在可以开始讨论最后两个参数了。虽然我们知道余下的两个参数之间有依赖关系，从而不能分解成为两个边缘分布的乘积，但是我们依然可以根据product-rule将其分解成为：

‍

现在，我们从之前的求解式中将只含有这两个变量的部分提取出来，于是我们得到：

‍

观察这个式子，我们发现其实对于K组参数，这个式子都是同样的，所以我们可以单独只考虑其中一组变量:

‍

我们对两边同时进行指数运算，则有：

‍

现在我们来分别看看这些分布的形式：

‍
‍‍

其中，B是Wishart分布的归一化常数

其中：

‍

我们注意上面这个式子，它的指数部分，展开之后，可以得到：

‍

观察这个式子，我们发现，其中关于mu的二阶式和一阶式，也就是上面这个式子的前三项，和mu本身的分布合并，可以化归成为一个新的Gaussian分布；而上面式子的最后一项，则可以被Lambda的Wishart分布所吸收合并，成为一个新的Wishart分布。这样，我们就找到了这两个参数的分布形式，他们是一个新的Gassian-Wishart分布：

‍

其中，定义了：

‍

从之前的文章中，我们已经得到了所有需要求解的参数的优化分布的形式，分别为：

‍

但是，我们从这些分布的表达式中（参见之前的文章），可以发现这些式子并不能够直接求解。这是因为各个参数之间相互耦合，从而导致得到的不是一个直接可以得到的解，所以我们需要进行迭代求解，正如我们在之前所描述的一样。我们观察这三组参数的表达形式，我们会发现，Z的求解依赖于r这个变量，而r这个变量的求解依赖于其余的所有参数。我们再看其他的参数，这些参数的求解依赖于r。从而我们得到了这个求解过程中的耦合部分。所以我们可以得到一个初步的求解迭代过程：

1. 初始化所有的参数，包括Z,r,pi,mu,Lambda等控制参数以及其超参数；

2. 保持pi,mu,Lambda等控制参数不变，根据表达式，求解r，进而求解Z。

3. 保持r和Z不变，根据表达式求解pi,mu,Lambda等控制参数。

如此不断往复，直至结果达到收敛精度要求或者超过一定迭代次数为止。

到这一步，我们可以基本认为，这个问题得到了解决。但是其中还有很多细节，我并没有在文中给予详细的解答，对于迭代过程的求解，也并不是一句话就可以带过的。

我们现在回头再去观察这个问题，我们会发现一个有趣的地方。那就是我们所求解的优化分布的形式，和我们所提出来的prior的形式是完全相同的。这是一个偶然现象，还是必然呢？答案是，在这个问题中，这是一种必然的过程，这是因为 我们选择的就是所希望求解分布的共轭先验(conjugate prior)。我简单解释一下这个概念：

对于一个给定的分布p(X|W)，我们可以寻找其一个先验分布p(W)，使得该先验和似然函数的乘积与先验分布有相同的函数形式，而我们知道，后验分布p(W|X)正比于先验和似然函数的乘积，从而与先验有相同的函数形式。

这样一个共轭先验的好处，是使得我们可以不断地重复先验转向后验的过程，使得我们可以不断利用已有的数据去理解新的数据，而后将它们放在一起，都作为已有的数据，再去理解新的数据，如此不断往复。而且共轭先验的函数形式也让数学形式上的分析变得更为容易，我们可以只需要考虑整个分布的一些重要的有特征的部分，而不需要对于其归一化常数等不重要的部分进行多次计算，只需要最后的时候根据函数形式进行对应就可以了。

而一个有意思的地方在于，对于指数家族函数的分布来说，每一个都存在一个对应的共轭先验，我简单介绍一下，对于形式为如下的分布，都可以成为指数家族分布：

‍

x可以为标量，也可以为矢量。u(x)为x的某种形式a的函数，而eta称作natural parameters，其函数g(eta)可以看做是一个归一化系数。

现在，我们为参数引入一个先验：

‍

而我们给定一个数据集，也可以计算其似然值：

‍

其中

‍

这样，我们将先验和似然函数相乘，可以得到：

‍

而这个函数，与先验函数具有相同的函数形式。这时候，我们就找到了一个共轭先验。而我们的原函数，是指数家族函数分布的一般形式，这也就意味着，每一个指数家族函数分布，都有其对应的共轭先验。