zoj 3862 Intersection (技巧题)
Edward has 2n points on the plane conveniently labeled with 1,2,…,2n. Each point is connected exactly with another point by a segment.
Edward finds that some segments intersecting with some others. So he wants to eliminate those intersections with the following operation: choose two points i and j (1 ≤ i, j ≤ 2n) and swap their coordinates.
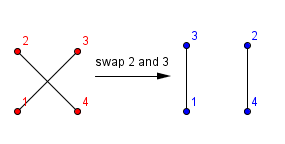
For example, Edward has 4 points (0, 0), (0, 1), (1, 1), (1, 0). Point 1 is connected with point 3 and point 2 is connected with 4. Edward can choose to swap the coordinates of point 2 and point 3.
Edward wants to know whether it is possible to use at most n + 10 operations to achieve his goal.
No two points coincide and no three points are on the same line.
Input
There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case:
The first line contains an integer n (1 ≤ n ≤ 100000).
Each of the following 2n lines contains 2 integers xi, yi which denotes the point (xi, yi). (|xi|, |yi| ≤ 109).
Each of the following n lines contains 2 integers ai, bi (1 ≤ ai, bi ≤ 2n, ai ≠ bi), which means point ai and point bi are connected by a segment.
The sum of values n for all the test cases does not exceed 300000.
Output
For each test case, print a line containing an integer m, indicating the number of operations needed. You must assure that m is no larger than n + 10. If you cannot find such a solution, just output "-1" and ignore the following output.
In the next m lines, each contains two integers i and j (1 ≤ i, j ≤ 2n), indicating an operation, separated by one space.
If there are multiple solutions, any of them is accepted.
Sample Input
1 2 0 0 0 1 1 1 1 0 1 3 2 4
Sample Output
1 2 3http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5474
给出n条线段, 每次可以选择两个点交换他们的坐标. 要求一个不超过n+10步的操作序列, 使得最终没有线段相交.
最不可能的错误可能是最可能的错误。30多次WA就是一个数组开小了( ̄^ ̄)ゞ
#include<iostream>
#include<algorithm>
#include<string>
#include<map>
#include<vector>
#include<cmath>
#include<string.h>
#include<stdlib.h>
#include<cstdio>
#include <ctime>
#include <cstdlib>
#define ll long long
#define mod 998244353
using namespace std;
struct node{
int a,b,c;
};
node x[200001];
int ip[200001];
int f[200001];
vector<pair<int,int> > r;
int cmp(node a,node b){
if(a.a!=b.a)
return a.a<b.a;
else
return a.b<b.b;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
r.clear();
int n,d,e;
scanf("%d",&n);
for(int i=1;i<=2*n;++i){
scanf("%d%d",&x[i].a,&x[i].b);
x[i].c=i; //名字
}
sort(x+1,x+2*n+1,cmp);//保证了绝对不会有两条线段相交(可以这样做的原因是题目放宽了n+10的限制)
for(int i=1;i<=2*n;++i)
ip[x[i].c]=i; //ip[名字]=位置
for(int i=1;i<=n;++i){
scanf("%d%d",&d,&e);
f[d]=e; //f[名字]=名字
f[e]=d;
}
for(int i=1;i<=2*n;i+=2){
int u=x[i].c,v=x[i+1].c; //不知道为什么,不用u,v代替这两个值就WA了
if(f[x[i].c]!=x[i+1].c){
r.push_back(make_pair(f[x[i].c],x[i+1].c));
swap(x[ip[f[u]]].c,x[i+1].c);
swap(ip[f[u]],ip[v]);
}
}
printf("%d\n",r.size());
for(int i=0;i<r.size();++i)
printf("%d %d\n",r[i].first,r[i].second);
}
return 0;
}