机器学习基础(林軒田)笔记之二
机器学习基础(林軒田)笔记之二
Learning to Answer Yes/No
本节课主要介绍了感知学习算法(PLA).
前景回顾:
第一节课讲了机器学习的定义,机器学习算法A从数据集D和假设集H中找到映射函数g。
一.Perceptron Hypothesis Set
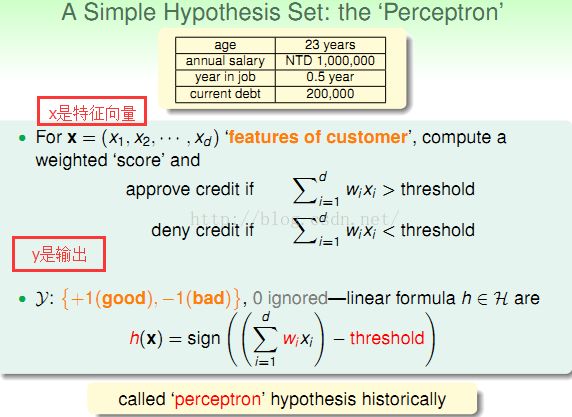
此部分,作者以银行是否为客户办理信用卡问题引入PLA算法,该算法的本质是一个线性分类器,针对所给的特征向量,给出Yes/No。
先将用户信息量化成特征向量,然后乘以权重向量,最后与一个阈值作比较,从而对结果进行分类。
进一步化简:
h(x)既是目标函数。
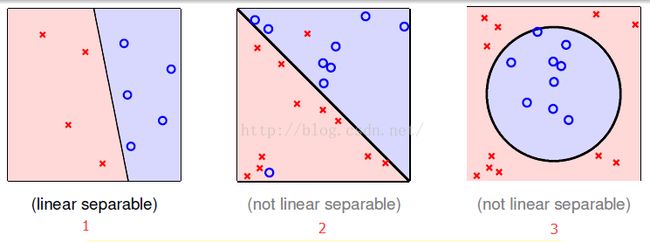
以一个二维平面的分类问题为例:
二.Perceptron Learning Algorithm (PLA)
在上节中我们给出了假设集H的表示,本节主要介绍利用PLA算法的迭代求解过程即从H中选择g的过程。
g(x)的判定条件:如果我们能够是的g对所有的输入所得到的输出与f对所有的输入所得到的输出一致,我们就认为这
样的g(x)是不错的。
难点:H(x)是无穷多的,因为权值w有无数种取值。
方法:一步一步的修正错误的分类,在二维平面中可以想象成一条初始的直线,在经过不断的纠正它的错误(就是旋转平移之类的)使得最终的结果可以达到希望的效果,也就是通过不断的修正权值向量来使其接近目标函数。
首先我们在设置初始w0(这是一个向量),比如设置为0向量,然后使用训练样本来将权值向量修正的更接近目标函数f。其修正步骤如下:
上图中详细表述了PLA的求解过程,其中右侧的向量图生动的表现了权值向量的求解过程。上面的向量图表示在标记本身为+1时,权值向量w与特征向量的内积结果为-1。此时,对权值向量的修改方式为:权值向量加上一个标记y和输入向量的乘积,得到一个新的权值向量,可以看出新的权值向量和输入向量的相乘之后符合了标记的要求。下面的向量图与上面的向量图恰好相反,并且两种情况可以合二为一,如左侧标记出的公式所示。
如此重复查找错误样本和修改加权向量,直到在整个样本中再也找不到g(x)不等于f(x)的样本为止,此时得到的加权向量,即为我们想要的最终g(x)。
三.Guarantee of PLA
本节主要证明PLA算法收敛并且有最优解。
PLA可行的必要条件:样本线性可分。
线性可分:
我们需要证明在线性可分的情况下,权值向量在经过一段时间的修正会停止,修正次数会有一个上界。
首先我们考虑是否每次修正都可以使得权值向量变得更好,就是是否会更接近未知的目标函数所表示的向量。我们先假设目标函数的权值向量为wf,可以求解出两个向量相似度的度量方式有很多,其中比较常用的一种方式就是求两个向量的内积,于是我们对wf和wt做内积。其中T表示为停止时的次数,如上图所示,我们得出wt在逐渐向wf靠拢。并且,最终迭代得(其中,w0=0):
1
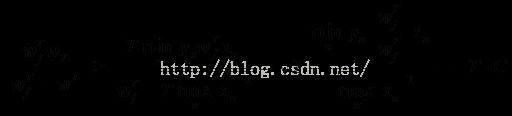
直接使用这两个向量做内积,其内积越大并不能代表这两个向量越接近,因为向量本身的变长也可以导致这一现象。因此我们需要求解的是这两个向量做归一化之后的内积,这时它俩的内积有了上界即为1,上图中公式1所示。
上图中公式1给出了WT的模的求法,并且最终迭代得:
进一步:
可以看出权值向量和目标函数内积会以的速度不断的增长,但是这种增长不是没有限制的,它最多只能等于1。
进而:
四.Non-Separable Data
本节主要分析线性不可分的情况(PLA算法的不足),并且之处克服缺点的方法。
上一节我们介绍了PLA这个算法一定会停下来这一结论,是建立在存在一个目标函数,可以将所有的数据点都线性分开这个假设的基础之上。
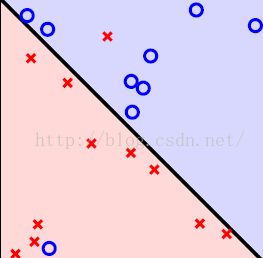
对于给定数样本数据我们应如何确定是否线性可分?比如一个PLA算法运行了很长时间仍然没有停止,此时存在两种可能性,一是该数据集是线性可分的,但是还没有运行结束;另一种,压根就不存在一条直线可以将数据集分开,就是压根这个算法就不会终止。假如是后者又该如何处理?
出现不可分的一种可能是从未知目标函数中产生的训练样本存在噪音(noise),如录入样本时有人工的错误等情况导致数据本身不正确,使得最终本可以线性可分的样本集变得线性不可分了。
而噪音占整个数据集的比例一般不会太大:
一种新的思路是找出犯错最少的权值向量 :
这里介绍一个叫pocket的算法,它的本质是一种贪心算法,做一简单的介绍:
1. 随机的初始化一个权值向量w
2. 随机的使用n个点中的一个点去发现是否有错误(此处与cyclic PLA使用的循环方式有所不同,不是按顺序一个一个的查看是否符合条件,而是在n个点中随机的抽取,这种方式可以增加其寻找最优解的速度)
3. 和PLA一样进行修正.
4. 如果有了修正,则计算出刚刚修正过的权值向量和上一个权值向量到底谁犯的错误比较少,将少的保留重复第2步到第4步的动作。